矩阵

由 $m * n$ 个元素排成的 $m$ 行 $n$ 列的表称为矩阵，其表现形式如下：

$\begin{pmatrix} a_{11}&a_{12}&a_{13}&\cdots&a_{1n}\\ a_{21}&a_{22}&a_{23}&\cdots&a_{2n}\\ \vdots&\vdots&\ddots&\ddots&\vdots\\ a_{m1}&a_{m2}&a_{m2}&\cdots&a_{mn} \end{pmatrix}$

行数与列数相等的矩阵称为方阵。

矩阵的特点：初始化后只能对元素进行获取和修改操作；不能对元素进行删除和新增操作。

矩阵的压缩存储

通常将矩阵看做一个二维数组，采用二维数组的存储方式存储矩阵：按行优先顺序存储、按列优先顺序存储。

矩阵中相同元素居多且呈某种分布规律，或者零元素过多时，采用顺序存储会造成空间的浪费，因此对矩阵进行压缩存储：多个相同的元素只分配一个存储空间，零元素不占用存储空间。

常见的压缩存储的特殊矩阵：对称矩阵、对角矩阵、三角矩阵、稀疏矩阵

对角矩阵的压缩存储

$n * n$ 的方阵中所有非零元素都集中在以主对角线为中心的带状区域中，区域外的值为 0，此时称该矩阵为对角矩阵。

对角矩阵的压缩方式：以行为主存储、以对角线的顺序为主存储

以行为主存储

三角矩阵的压缩存储

对角线以上（以下）的数据元素（不包含对角线）全部为常数 $C$ 的矩阵称为上（下）三角矩阵。

扫描二维码关注公众号，回复： 9700214 查看本文章

上三角矩阵：
$\begin{pmatrix} a_{11}&a_{12}&\cdots&a_{1n}\\ c&a_{22}&\cdots&a_{2n}\\ \vdots&\vdots&\ddots&\vdots\\ c&c&\cdots&a_{nn} \end{pmatrix}$

下三角矩阵：
$\begin{pmatrix} a_{11}&c&\cdots&c\\ a_{21}&a_{22}&\cdots&c\\ \vdots&\vdots&\ddots&\vdots\\ a_{n1}&a_{n2}&\cdots&a_{nn} \end{pmatrix}$

三角矩阵的压缩方式：

• 重复元素 $c$ 共享一个元素存储空间，当 $c=0$ 时无需存储；
• 其他元素按行优先或按列优先存储，共占用 $\frac {n(n+1)}2 +1$ 个元素存储空间。

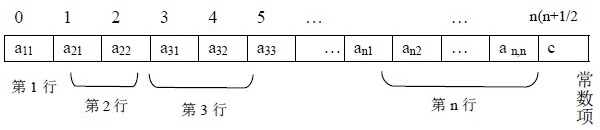
上三角矩阵压缩存储：

下三角矩阵压缩存储：

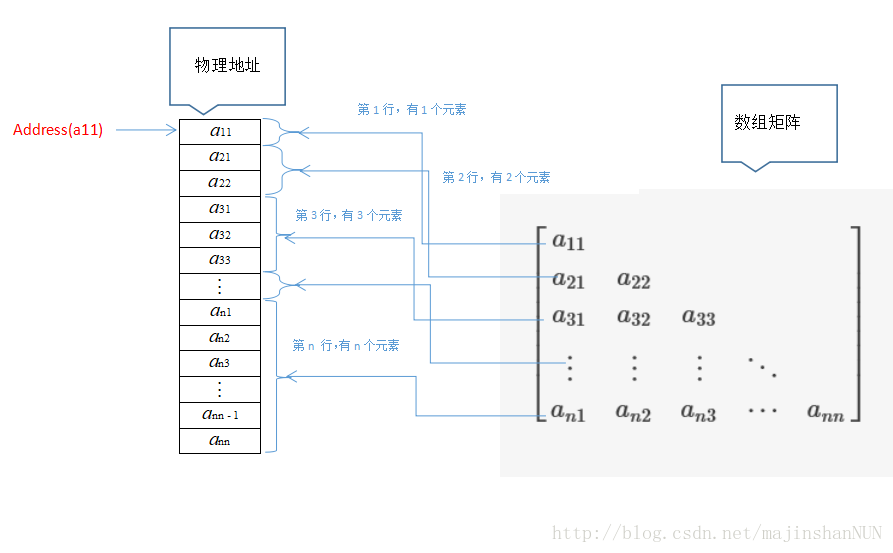
对称矩阵的压缩存储

对称矩阵： $n * n$ 的矩阵 $a$ 满足 $a_{ij}=a_{ji}(1\ge i,j\ge n)$。

对称矩阵的压缩方式：对每一对对称元素分配一个存储空间，存储空间由 $n^2$ 压缩为 $n(n+1)\over 2$ ；按行（列）优先顺序，只存储对角线以下（或以上，包含对角线）的数据元素。

假设一个 $n$ 阶对称矩阵存储结构对应一个一维数组 $a[{n(n+1)\over 2}]$ 个元素空间，则 $a[k]$ 与矩阵元素 $a_{ij}$ 的对应关系为：
$k= \begin{cases} {i(i-1)\over 2} + j -1, & i\ge j\\ {j(j-1)\over 2} + i -1, & i\lt j \end{cases}$
因此：

• 任意一个矩阵下标 $(i,j)$ 均可在一维数组 $a$ 中找到矩阵元素 $a_{i,j}$
• 对任意 $k(0 \ge k \ge {n(n-1)\over 2} )$ 都能确定 $a[k]$ 在矩阵中的位置 $(i,j)$。

稀疏矩阵的压缩存储

$稀疏矩阵：m * n$ 的矩阵有 $t$ 个非零元素，非零元素的个数较少（小于 5% ），且非零元素的分布没有规律。
$\begin{pmatrix} 0&a_{12}&0&\cdots&0\\ a_{21}&0&0&\cdots&0\\ 0&0&0&\cdots&a_{3n}\\ \vdots&\vdots&\ddots&\vdots\\ 0&a_{n2}&0&\cdots&0 \end{pmatrix}$

稀疏矩阵只存储矩阵中的非零元即可，故可以采用三元组来存储稀疏矩阵，三元组中元素：

• 第一行存储：矩阵的行数、列数、非零元素的总个数；
• 第一行之后，每行存储一个矩阵中的非零元信息：非零元所在的行位置、列位置、元素值。
  稀疏矩阵与三元组一一对应，若稀疏矩阵中有 $k$ 个非零元，则三元组有 $k+1$ 行元素。

稀疏矩阵与三元组常见操作：将稀疏矩阵转换成三元组存储、将三元组转换成唯一的稀疏矩阵。

稀疏矩阵 $A$ 的元素如下：
$\begin{pmatrix} 0&2&0&0&0&0&0\\ 0&0&0&0&0&0&0\\ 0&0&0&0&0&0&0\\ 0&0&0&4&0&0&0\\ 0&0&0&0&0&0&0\\ 16&0&0&0&0&0&0\\ 0&0&0&0&0&0&0 \end{pmatrix}$
压缩存储后的三元组为：
$\begin{pmatrix} 7&7&3\\ 1&2&2\\ 4&4&4\\ 6&1&16 \end{pmatrix}$

应用实例

• 使用稀疏矩阵保存类似的二维数组（如棋盘、地图等）
• 存储稀疏矩阵，或者恢复存储的二维数组

参考

• 《数据结构(C语言版)》 严魏敏、吴伟民著
• 《数据结构(第3版)》 刘大有等著