• 【总目录】信号与系统 学习笔记 Signals and Systems with Python
• 信号与系统(Python) 学习笔记摘录 (1) 信号简介 Intro
• 2. 傅里叶 Fourier
  • 2.1. 傅里叶级数
    • 2.1.1. 矢量正交
    • 2.1.2. 信号正交
    • 2.1.3. 三角函形式
    • 2.1.4. 指数形式
    • 2.1.5. 频谱
    • 2.1.6. Sa 函数
    • 2.1.7. 频谱特点
    • 2.1.8. 周期信号的功率
    • 2.1.9. 频带宽度
  • 2.2. 傅里叶变换
    • 2.2.1. 常用函数的傅里叶变换
    • 2.2.2. 常用函数的傅里叶变换汇总
    • 2.2.3. 性质
    • 2.2.4. 卷积定理
    • 2.2.5. 微积分特性
    • 2.2.6. 相关定理

2. 傅里叶 Fourier

2.1. 傅里叶级数

2.1.1. 矢量正交

• 两正交矢量的内积为零: $\vec{V_1} \cdot \vec{V_2} = \lvert V_1 \rvert \cdot \lvert V_2\rvert \cos 90^\circ = 0$
• 正交矢量集: 由两两正交的矢量组成的矢量集合。
• 矢量正交分解: 任意 $N$ 维矢量可有 $N$ 维度 正交坐标系表示:
  $\vec{V} = c_1\vec{V_1} + c_2\vec{V_2} + \cdots + c_r\vec{V_r} + \cdots + c_n \vec{V_n}, \, (V_i \cdot V_j = 0, \, i \neq j)$
  $c_r =\frac{\lvert V \rvert \cos \theta_r}{\lvert V_r \rvert} = \frac{\vec{V} \cdot \vec{V_r}}{\vec{V_r}\cdot\vec{V_r}}$

2.1.2. 信号正交

• 定义: 在 $(t_1,t_2)$ 区间的两个函数 $\varphi_1(t)$ 和 $\varphi_2(t)$, 若满足
  $\int_{t_1}^{t_2} \varphi_1(t) \varphi_2^* (t)d t = 0, \, \text{(两函数的内积为0)}$
  则称 $\varphi_1(t)$ 和 $\varphi_2(t)$ 在区间 $(t_1, t_2)$ 内正交

  • 实函数正交 $\int_{t_1}^{t_2} \varphi_1(t) \varphi_2 (t)d t = 0, \, \text{(两函数的内积为0)}$

• 正交函数集: 若 $n$ 个函数 $\varphi_1(t), \varphi_2(t), \cdots , \varphi_n(t)$ 构成一个函数集, 当这些函数在区间 $(t_1,t_2)$ 内满足
  $\begin{aligned}\int_{t_i}^{t_j} \varphi_1(t) \varphi_2^* (t)d t ={\begin{cases} 0,\, & i\neq j \\ K_j \neq 0 , \, & i=j \end{cases}}\end{aligned}$
  则称此函数为函数集在区间 $(t_1,t_2)$ 上的正交函数集。

  • 若 $K_i= 1$, 称为标准正交函数集。

• 完备正交函数集: 如果在正交函数集 $\{ \varphi_1(t), \varphi_2(t), \cdots , \varphi_n(t) \}$ 之外，不存在任何函数 $\varphi(t) (\neq0)$ 满足
  $\int_{t_1}^{t_2} \varphi(t) \varphi_i^* (t)d t = 0, \, (i = 1,2,\cdots, n)$
  则称此函数集为完备正交函数集。

• 信号的正交分解: 设由 $n$ 个函数 $\varphi_1(t), \varphi_2(t), \cdots, \varphi_n(t)$ 在区间 $(t_1,_2)$ 构成一个正交函数空间。将任一函数 $f(t)$ 用这 $n$ 个正交函数的线性组合来近似, 可表示为
  $f(t) \approx C_1\varphi_1(t) + C_2\varphi_2(t) + \cdots + C_i\varphi_i(t) + \cdots + C_n\varphi_n(t) = \displaystyle \sum^{n}_{j=1} C_j \varphi_j(t)$

  • 使误差的均方误差 $\overline{\varepsilon^2} = \displaystyle \frac{1}{t_2-t_1} \int_{t_1}^{t_2}\big[f(t)-\sum^n_{j=1} C_j\varphi_k(t)\big]^2 dt$ 最小,
    要令 $\displaystyle\frac{\partial\overline{\varepsilon^2}}{\partial C_i} = 0$ 即
    $\displaystyle\overline{\varepsilon^2} = \frac{1}{t_2-t_1}\Big[\int^{t_2}_{t_1} f^2(t)dt - \sum^n_{j=1} \int^{t_2}_{t_1}\big[C_j\varphi_j(t)\big]^2dt\Big]\geq0$
    • 可知 在正交函数去近似 $f(t)$ 时, 所取的项数越多, 即 $n$ 越大, 则均方误差越小。当 $n\to\infty$ 时 (完备正交函数集), 均方误差为零。

• 广义傅里叶系数:

  • 复变函数: $C_i = \displaystyle\frac{\int^{t_2}_{t_1}f(t)\varphi_i^*(t)dt}{\int^{t_2}_{t_1}\varphi_i(t)\varphi_i^*(t)dt} = \frac{1}{K_i}\int^{t_2}_{t_1}f(t)\varphi_i^*(t)dt$

• 帕什瓦尔 Parseval 方程:
  $\int^{t_2}_{t_1} f^2(t)dt = \sum^\infty_{i=1} \int^{t_2}_{t_1}\big[C_i\varphi_j(t)\big]^2dt$

  • 物理意义: 在区间 $(t_1,t_2)$, 信号 $f(t)$ 所含由的能量恒等于此信号在完备正交函数集 中各正交分量能量之和, 即 能量守恒定理 也称 帕什瓦尔定理。
  • 数学本质: 矢量空间信号正交变换的范数不变性。

2.1.3. 三角函形式

• 三角函数集 $\{ 1, \cos(n\Omega t), \sin(n\Omega t), n = 1,2,\cdots\}$

• 三角形式的傅里叶级数: 设周期信号为 $f(t)$, 其周期为 $T$, 角频率为 $\Omega = 2\pi/T$, 当满足 Dirichlet 狄里赫利 条件时, 可展开为
  $\begin{aligned}f(t) = \displaystyle \frac{a_0}{2} + \sum^\infty_{n=1} a_n \cos(n\Omega t) + \sum^\infty_{n=1} b_n \sin(n\Omega t) \\ \text{合并 n 次正余弦分量} \to f(t) = \frac{A_0}{2} + \sum^\infty_{n=1} \big(A_n \cos(n\Omega t) + \varphi_n\big) \\ \begin{cases} A_n & = \sqrt{a^2_n + b^2_n} \\ \varphi_n & = - \arctan \frac{b_n}{a_n} \end{cases} \begin{cases} a_n & = A_n \cos \varphi_n \\ b_n & = - A_n \sin \varphi_n \end{cases} \end{aligned}$

  • 系数 $a_n, b_n$ 称为傅里叶系数
  • 直流分量系数: $\displaystyle\frac{a_0}{2} = \frac{1}{T}\int^{\frac{T}{2}}_{-\frac{T}{2}}f(t)dt$
  • 余弦分量系数: $\displaystyle a_n = \frac{2}{T}\int^{\frac{T}{2}}_{-\frac{T}{2}}f(t)\cos(n\Omega t)dt$
  • 正弦分量系数: $\displaystyle b_n = \frac{2}{T}\int^{\frac{T}{2}}_{-\frac{T}{2}}f(t)\sin(n\Omega t)dt$
  • 直流分量 $A_0/2$ , 基波 (一次谐波) $A_1 \cos(\Omega t + \varphi_1)$ , n次谐波 $A_n \cos(n \Omega t + \varphi_n)$

Dirichlet 狄里赫利 条件:

1. f(x) must absolutely integrable over a period. 在单个周期内绝对可积
   $\int^T_0 \lvert f(t) \rvert dt < \infty$
2. f(x) must have a finite number of exterma in any given interval, i.e. there must be a finite number of maxima and minima in the interval. 在一个周期内，函数有有限个极大值或极小值。
3. f(x) must have a finite number of discontinues in any given interval, however the discontinuity cannot be infinite. 函数在任意有限区间内连续，或只有有限个第一类间断点
4. f(x) must be bounded.

• 谐波特性:

  1. $f(t)$ 为偶函数 $\big(f(t)=f(-t)\big)$ 时， $b_n = 0$ 展开为余弦级数
  2. $f(t)$ 为奇函数 $\big(f(t)=-f(-t)\big)$ 时， $a_n = 0$ 展开为正弦级数
  3. $f(t)$ 为奇谐函数 $\big(f(t)=-f(t\pm T/2)\big)$ 时， $a_i= b_i = 0, \, (i=0,2,4,\cdots)$ 展开级数只含奇次谐波分量，不含偶次谐波分量。
  4. $f(t)$ 为偶谐函数 $\big(f(t)=f(t\pm T/2)\big)$ 时， $a_i= b_i = 0, \, (i=1,3,5,\cdots)$ 展开级数只含偶次谐波分量，不含奇次谐波分量。

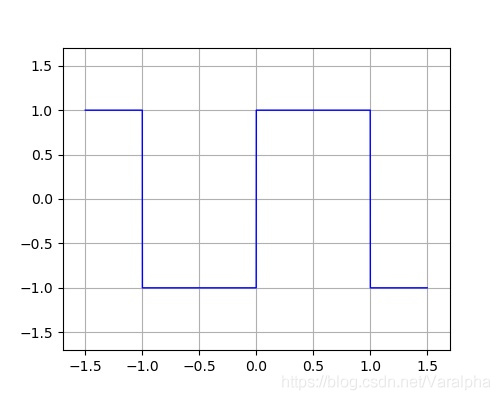
• 例：图示方波信号f(t) 为奇谐函数 展开为傅里叶级数
  
  解得: $\displaystyle f(t) = 0 + \frac{4}{\pi} \sum^n_{i=0}\big[\frac{1}{1+2i}\sin{\big((1+2i)\Omega t\big)}\big], \, \Omega = \frac{2\pi}{T}, \, T=2$
  

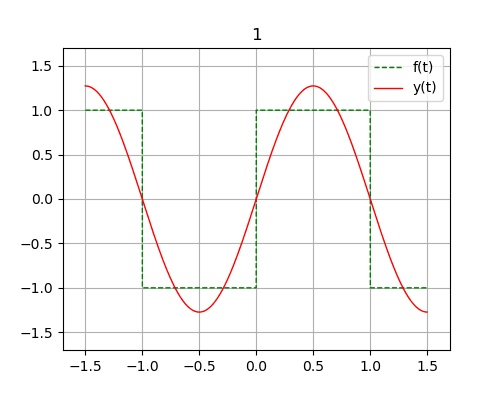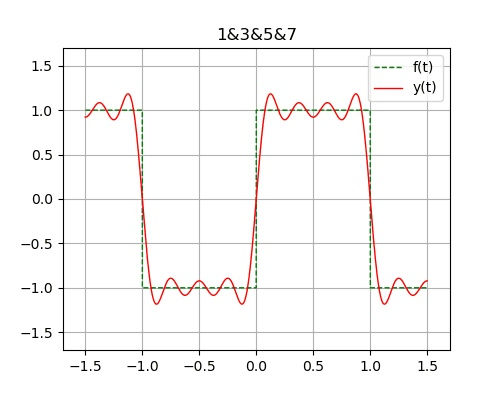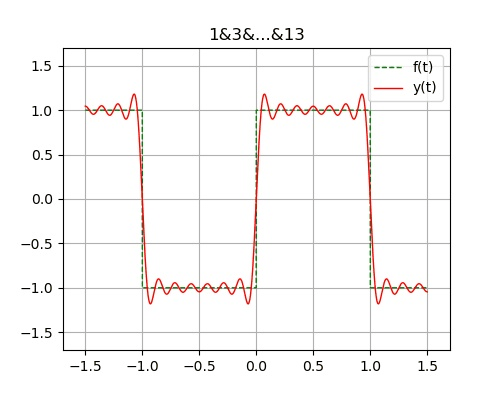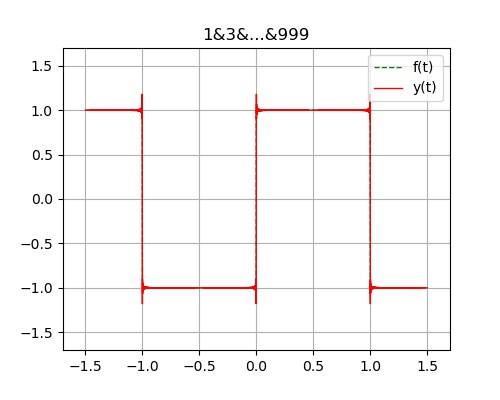
• 吉布斯现象: 在有限项傅里叶级数表示有间断点的信号时, 在间断点附近不可避免的会出现震荡和超调量。超调量的幅度不会随所取项数的增加而减小。只是随着项数的增多, 震荡频率变高, 并向间断点处压缩, 从而使它所占有的能量减小。当选取的项数很大时, 该超调量趋近于一个常数, 大约等于总跳变值的9%, 并从间断点开始以起伏震荡的形式逐渐衰减下去。

2.1.4. 指数形式

• 欧拉公式 Euler’s formula: $e^{\pm jt} = \cos(t) \pm j\sin(t)$

• 指数形式: 利用欧拉公式可得
  $\begin{aligned}\displaystyle f(t) & = \frac{A_0}{2} + \sum^\infty_{n=1} \big(A_n \cos(n\Omega t) + \varphi_n\big)\\ & = \frac{1}{2}\sum^{\infty}_{n=-\infty} A_n e^{j\varphi_n}e^{jn\Omega t} \\ & = \sum^{\infty}_{n=-\infty}e^{jn\Omega t} F_n, \, \big(F_n = \frac{1}{2} A_n e^{j\varphi_n} = \lvert F_n \rvert e^{j\varphi_n} = \frac{1}{2}(a_n-j b_n)\big) \end{aligned}$

• 复傅里叶系数 简称 傅里叶系数 为 $F_n$:

  • 利用欧拉公式可得 $\displaystyle F_n = \frac{1}{T} \int^{\frac{T}{2}}_{-\frac{T}{2}} f(t) e^{-jn\Omega t} dt$

2.1.5. 频谱

• $\lvert F_n \rvert$ 是 $n$ 的偶函数, 双边幅度谱的谱线高度为单边幅度谱的一半，关于纵轴对称; 而直流分量值不变。
• $\varphi_n$ 是 $n$ 的奇函数，双边相位谱可以由单边相位谱直接关于零点奇对称。

2.1.6. Sa 函数

$\text{Sa}(x) = \displaystyle\frac{\sin(x)}{x}$

• 对于脉冲幅度为 $1$, 宽度为 $\tau$, 周期为 $T$ 的周期矩形脉冲,
  $\begin{aligned}F_n &= \displaystyle \frac{1}{T}\int^{\frac{T}{2}}_{-\frac{T}{2}}f(t) e^{-jn\Omega t} dt \\ &= \frac{1}{T}\int^{\frac{T}{2}}_{-\frac{T}{2}}e^{-jn\Omega t} dt \\ &= \frac{\tau}{T}\text{Sa}\big(\frac{n\Omega \tau}{2}\big)\end{aligned}$

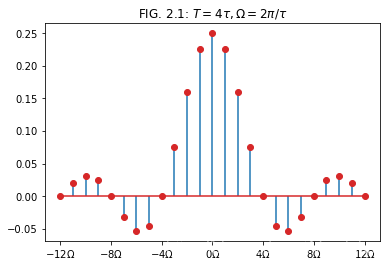
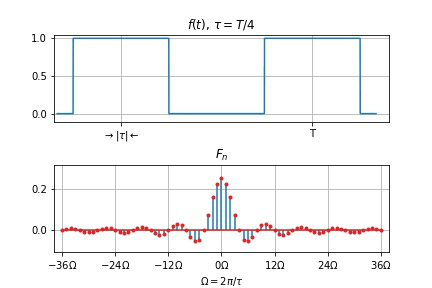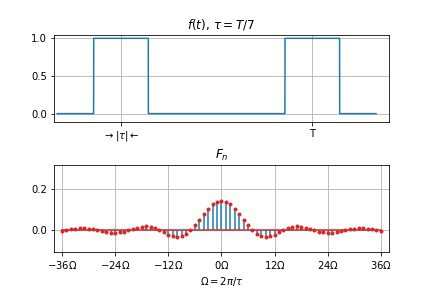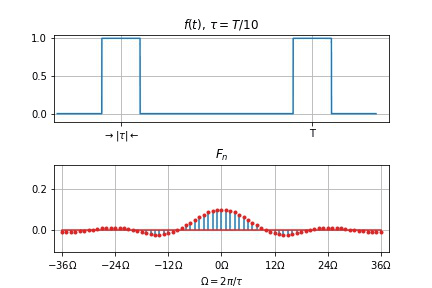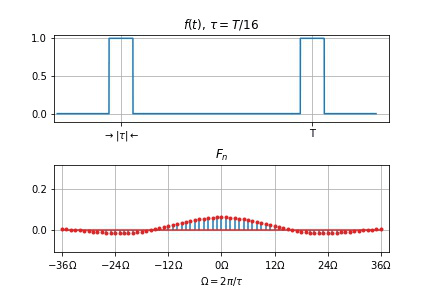
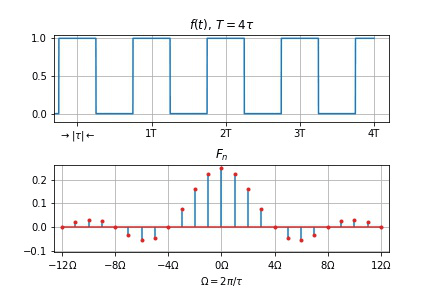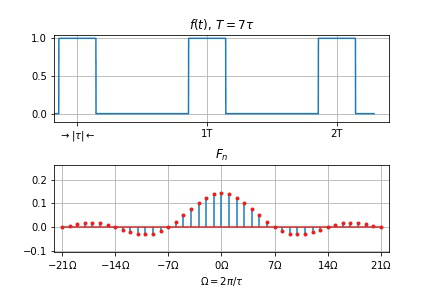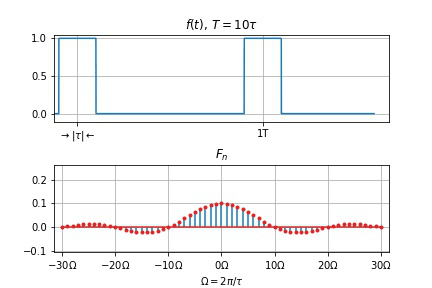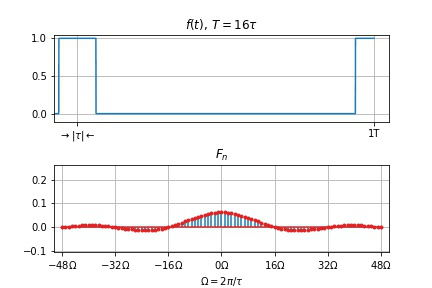
• 用 Python 画出 $T=4\tau, \displaystyle\Omega=\frac{2\pi}{\tau}$ 的频谱 $F_n$

    # 导入 需要的 library 库  
    import numpy as np # 科学计算
    import matplotlib.pyplot as plt # 画图工具
    import scipy.signal as sg # 导入 scipy 的 signal 库 命名为 sg
    
    # 用 Python 表示 
    def Sa(x):
        return np.divide(np.sin(x),x) if x != 0 else 1

    def F_n(T,ns,tau):
        omega = 2*np.pi/T
        return np.array([round(np.divide(tau,T)*Sa(np.divide(n*omega*tau, 2)),6) for n in ns])
    
    # 画图
    n = np.linspace(-12,12,25)
    y = F_n(8*np.pi, n, 2*np.pi)
    plt.stem(n, y, '-',label='f', markerfmt='C3o',  use_line_collection=True)
    plt.xticks(n[::4],[fr'${i*4}\Omega$'for i in range(-3,4)])
    plt.title(r'FIG. 2.1: $T=4\tau, \Omega = 2\pi/\tau$')
    plt.show()

2.1.7. 频谱特点

• 周期信号频谱的特点

  1. 离散性: 以基频 $\Omega$ 为间隔的若干离散谱线组成;
  2. 谐波性: 谱线仅含有基频 $\Omega$ 的整数倍分量;
  3. 收敛性: 整体趋势减小。

• $T$ 不变, $\tau$ 变小

  • 谱线间隔 $\Omega$ 不变
  • 幅度下降
  • 零点右移动, 两零点间谱线数目 $T/\tau$ 增加

• $\tau$ 不变, $T$ 变大
  • 谱线间隔 $\Omega$ 变小,
  • 幅度下降,
  • 频谱变密。

• 当 $T \to \infty$ 时, 谱线间隔 $\Omega = 2\pi/T \to 0$, 谱线幅度 $\to 0$, 周期信号的离散频谱过渡为非周期信号的连续频谱。

  • 频谱密度函数:
    $\begin{aligned}F_n &= \displaystyle \frac{1}{T}\int^{\frac{T}{2}}_{-\frac{T}{2}}f(t) e^{-jn\Omega t} dt \\ T & \to \infty \, \text{时} \\ \Omega & \to d \Omega \; \text{(无穷小量)} \\ n\Omega &\to \omega \; \text{(离散}\to \text{连续)} \\ F(j\omega) & = \lim_{T\to\infty} F_nT \; \text{(单位频率上的频谱)} \\ &= \lim_{T\to\infty}\int^{\frac{T}{2}}_{-\frac{T}{2}}f(t) e^{-jn\Omega t} dt \\ &=\int^{\infty}_{-\infty} f(t) e^{-j\omega t} dt \end{aligned}$
  • $F(j\omega)$ 称为频谱密度函数，简称频谱密度或频谱。

• 收敛性分析:

  1. 振幅是收敛的: 信号的能量主要集中在低频分量中
  2. 收敛具有不同速度: 信号连续光滑， 幅度谱快速衰减。
     • 低频反应信号的主要信息, 高频表现细节。

     方波的幅度谱 按照 $\frac{1}{n}$ 缓慢衰减
     三角波的幅度谱 按照 $\frac{1}{n^2}$ 缓慢衰减

2.1.8. 周期信号的功率

• 周期信号一般为功率信号, 其平均功率为:
  $\begin{aligned}P & =\frac{1}{T} \int^{\frac{\tau}{2}}_{-\frac{\tau}{2}}f^2(t)dt \\ &=\frac{1}{T} \int^{\frac{\tau}{2}}_{-\frac{\tau}{2}} \Big[ \frac{A_0}{2} + \sum^\infty_{n=1} \big(A_n \cos(n\Omega t) + \varphi_n\big)\Big]^2 dt \\ &= \frac{A_0}{2}^2 + \sum^\infty_{n=1} \frac{1}{2} A_n^2\\ &= \lvert F_0 \rvert ^2 + 2 \sum^\infty_{n=1} \lvert F_n\rvert^2 \\ &= \sum^\infty_{n=-\infty} \lvert F_n\rvert^2 \end{aligned}$
  • 这是 帕斯瓦尔定理(Parseval’s theorem) 在傅里叶级数情况下的具体体现。
  • 含义: 周期信号平均功率 $=$ 直流和谐波分量平均功率之和。
  • 表明: 对于周期信号, 在时域中求得的信号功率与在频率中求得的信号功率相等。

2.1.9. 频带宽度

• 在满足一定失真条件下, 信号可以用某段频率范围的信号来表示, 此频率范围称为频段宽度。

• 第一个零点 (例图 FIG 2.1 $[-4\Omega, 4\Omega]$) 集中了信号 绝大部分能量（平均功率）由频谱的收敛性可知，信号的功率集中在低频段。

  例图中 第一个零点以内各分量的功率占总功率 约 90.3%

1. 一般把第一个零点作为信号的频带宽度。记为: $B_\omega = \frac{2\pi}{\tau}$ or $B_f = \frac{1}{\tau}$ 宽度与脉冲成反比。
2. 对于一般周期信号，将幅度下降为 $\frac{1}{10}\lvert F_n\rvert _{\text{max}}$ 的频率区间定义为频带宽度。
3. 系统的通频带 $>$ 信号的带宽，才能不失真。

2.2. 傅里叶变换

$f(t) \longleftrightarrow F(j\omega)$
$F(j\omega) =\int^{\infty}_{-\infty} f(t) e^{-j\omega t} dt = \mathfrak{F}\big[f(t)\big]$
$f(t) =\displaystyle \frac{1}{2\pi} \int^{\infty}_{-\infty} F(j\omega) e^{j\omega t} d\omega = \mathfrak{F}^{-1}\big[F(j\omega)\big]$

• $F(j\omega)$ 称为 $f(t)$ 的傅里叶变换

• $F(j\omega)$ 一般是复函数，写为
  $F(j\omega) = \lvert F(j\omega)\rvert e^{j\varphi(\omega)}$

• $\lvert F(j\omega)\rvert \sim \omega$ 幅度频谱，频率 $\omega$ 的偶函数

• $\lvert \varphi(\omega)\rvert \sim \omega$ 相位频谱，频率 $\omega$ 的奇函数

• Remark:

  1. 函数 $f(t)$ 的傅里叶变换存在的充分条件:
     $\int^{\infty}_{-\infty} \lvert f(t)\rvert dt < \infty$
  2. 下列关系还可方便计算一些积分:
     $F(0) = \int^{\infty}_{-\infty} f(t) dt$
     $f(0) = \frac{1}{2\pi} \int^{\infty}_{-\infty} F(j\omega) d\omega$

2.2.1. 常用函数的傅里叶变换

1. 单边指数函数
   $\begin{aligned} f(t) = e^{-\alpha t} \varepsilon(t) = \begin{cases} e^{-\alpha t} \; & t>0 \\ 0 \; & t<0 \end{cases}\; \alpha>0 \end{aligned}$

$\begin{aligned} F(j\omega) = \displaystyle \frac{1}{\alpha + j\omega} \end{aligned}$

2. 双边指数函数
   $\begin{aligned} f(t) = e^{-\alpha \lvert t\rvert} = \begin{cases} e^{-\alpha t} \; & t>0 \\ e^{\alpha t} \; & t<0 \end{cases}\; \alpha>0 \end{aligned}$

$\begin{aligned} F(j\omega) = \displaystyle \frac{2\alpha}{\alpha^2 + \omega^2} \end{aligned}$

3. 门函数(矩形脉冲) $g_\tau$
   $\begin{aligned} g_\tau(t) = \begin{cases}1 \; & \lvert t\rvert \leq \frac{\tau}{2} \\ 0 \; & \lvert t\rvert > \frac{\tau}{2} \end{cases} \end{aligned}$

$\begin{aligned} F(j\omega) = \tau \text{Sa} \Big\lgroup \displaystyle \frac{\omega\tau}{2} \Big\rgroup \end{aligned}$

4. 冲激函数 $\delta, \delta^\prime, \delta^{(n)}$
   $\begin{aligned} f(t) \longleftarrow& \longrightarrow F(j\omega) \\ \delta \longleftarrow& \longrightarrow 1 \\ \delta^\prime \longleftarrow& \longrightarrow j\omega \\ \delta^{(n)} \longleftarrow& \longrightarrow (j\omega)^n \end{aligned}$

5. 常数 1
   $\begin{aligned}1 \longleftarrow& \longrightarrow 2\pi\delta{(\omega)} \end{aligned}$

6. 符号函数
   $\begin{aligned} \text{sgn}(t)\longleftarrow& \longrightarrow \frac{2}{j\omega} \end{aligned}$
   $\begin{aligned} \text{sgn}(t) = \begin{cases}-1 \; & t<0 \\ 1 \; & t>0 \end{cases} \end{aligned}$

7. 阶跃函数 $\varepsilon$
   $\begin{aligned} \varepsilon(t)\longleftarrow& \longrightarrow \pi \delta(\omega) + \frac{1}{j\omega} \end{aligned}$
   $\begin{aligned} \varepsilon(t) = \begin{cases}0 \; & t<0 \\ 1 \; & t>0 \end{cases} \; = \frac{1}{2} + \frac{1}{2} \text{sgn}(t) \end{aligned}$

2.2.2. 常用函数的傅里叶变换汇总

$\begin{aligned} \displaystyle f(t) \longleftarrow& \longrightarrow F(j\omega) \\ 1 \longleftarrow& \longrightarrow 2\pi\delta{(\omega)}\\ e^{-\alpha t} \varepsilon(t)\longleftarrow& \longrightarrow \frac{1}{\alpha + j\omega}\\ e^{-\alpha \lvert t\rvert} \longleftarrow& \longrightarrow \frac{2\alpha}{\alpha^2 + \omega^2} \\ g_\tau(t) \longleftarrow& \longrightarrow \tau \text{Sa} \Big\lgroup \displaystyle \frac{\omega\tau}{2} \Big\rgroup\\ \delta \longleftarrow& \longrightarrow 1 \\ \delta^\prime \longleftarrow& \longrightarrow j\omega \\ \delta^{(n)} \longleftarrow& \longrightarrow (j\omega)^n \\ \varepsilon(t)\longleftarrow& \longrightarrow \pi \delta(\omega) + \frac{1}{j\omega}\\ \text{sgn}(t)\longleftarrow& \longrightarrow \frac{2}{j\omega}\\ \cos \omega_0 t \longleftarrow& \longrightarrow \pi \big[ \delta(\omega + \omega_0) + \delta(\omega-\omega_0)\big] \\ \sin \omega_0 t \longleftarrow& \longrightarrow j\pi \big[ \delta(\omega + \omega_0) - \delta(\omega-\omega_0)\big] \\ \end{aligned}$

2.2.3. 性质

• 线性性质

  • if $f_1(t) \leftrightarrow F_1(j\omega)$, $f_2(t) \leftrightarrow F_2(j\omega)$
    then $a\cdot f_1 + b\cdot f_2 \leftrightarrow a\cdot F_1 + b \cdot F_2$

• 奇偶性

  • if $f(t) \leftrightarrow F(j\omega)$
    then $f(-t) \leftrightarrow F(-j\omega)$

  若 $f(t)$为实偶函数, $F(j\omega)$为实偶函数
  若 $f(t)$为实奇函数, $F(j\omega)$为实奇函数

• 尺度变换

  • if $f(t) \leftrightarrow F(j\omega)$
    then $f(\alpha t) \leftrightarrow \frac{1}{\lvert \alpha \rvert}F(j\frac{\omega}{\alpha}), \alpha$ 为非零实数

  • $0<\alpha<1$ 时域扩展，频带压缩

  • $\alpha>1$ 时域压缩，频域扩展 $\alpha$ 倍

  • Remark:

    • 信号的持续时间与信号占有频带成反比，有时为加速信号的传递，要将信号持续时间压缩，则要以展开频带为代价。

• 对称性

  • if $f(t) \leftrightarrow F(j\omega), (\; t\to -\omega, \; \omega \to t)$
    then $F(j t) \leftrightarrow 2\pi f(-\omega)$

• 时移性 $t_0$

  • if $f(t) \leftrightarrow F(j\omega)$
    then $f(t \pm t_0) \leftrightarrow e^{\pm j \omega t_0}F(j\omega), \; t_0$ 为实常数
  • if $F(j\omega) = \lvert F(j\omega)\rvert e^{j \varphi(\omega)}$
    then $f(t \pm t_0) \leftrightarrow \lvert F(j\omega)\rvert e^{j[\varphi(\omega)\pm \omega t_0]}, \; t_0$ 为实常数
  • Remark:
    • 幅度频谱无变化，只影响相位频谱，相移 $\pm \omega t_0$

• 频移性 $\omega_0$

  • if $f(t) \leftrightarrow F(j\omega)$
    then $e^{\mp j\omega_0 t}f(t)\leftrightarrow F\big[j(\omega\pm\omega_0)\big], \; \omega_0$ 为实常数。
  • 频移特性的实质是频谱搬移，它是通信理论中信号调制与解调的理论基础。
  • $\cos(\omega_0 t)$ 调制信号——载波
  • $\omega_0$ 调制频率 —— 载频

2.2.4. 卷积定理

• 时域卷积:

  • if $f_1(t) \leftrightarrow F_1(j\omega), \;f_2(t) \leftrightarrow F_2(j\omega)$
  • then $f_1(t) \star f_2(t) \longleftrightarrow F_1(j\omega) F_2(j\omega)$

• 频域卷积:

  • if $f_1(t) \leftrightarrow F_1(j\omega), \;f_2(t) \leftrightarrow F_2(j\omega)$
  • then $\displaystyle f_1(t) f_2(t) \longleftrightarrow \frac{1}{2\pi}F_1(j\omega)\star F_2(j\omega)$

2.2.5. 微积分特性

• 时域微分:
  $f^{(n)} (t) \longleftrightarrow (j\omega)^n F(j\omega)$

• 时域积分:
  $\begin{aligned}\displaystyle \int^{t}_{-\infty} f(x) dx \longleftrightarrow \pi F(0)\delta(\omega) + \frac{F(j\omega)}{j\omega} \\ F(0) = F(j\omega)\Big\vert_{\omega = 0} = \int^{\infty}_{-\infty}f(t)dt \end{aligned}$

• 频域微分:
  $(-jt)^n f (t) \longleftrightarrow F^{(n)}(j\omega)$

• 频域积分:
  $\begin{aligned}\displaystyle \pi f(0)\delta(t) + \frac{f(t)}{-jt} \longleftrightarrow \int^{\omega}_{-\infty}F(jx)dx \\ f(0) = \frac{1}{2\pi}\int^{\infty}_{-\infty}F(j\omega)d\omega \end{aligned}$

2.2.6. 相关定理

• 相关函数

  • if $f_1(t) \leftrightarrow F_1(j\omega), \;f_2(t) \leftrightarrow F_2(j\omega)$
  • then
    $\begin{aligned}\displaystyle F\big[R_{12}(\tau)\big] &\longleftrightarrow F_1(j\omega) F_2^* (j\omega) \\ F\big[R_{21}(\tau)\big] &\longleftrightarrow F_1^*(j\omega) F_2 (j\omega)\end{aligned}$

• 自相关函数:
  $\begin{aligned}\displaystyle F\big[R(\tau)\big] = F(j\omega) F^* (j\omega)= \lvert F(j\omega)\rvert^2 \end{aligned}$