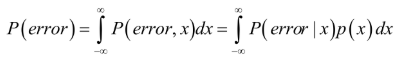对分类任务来说，在所有相关概率都己知的理想情形下，贝叶斯决策论考虑如何基于这些概率和误判损失来选择最优的类别标记.下面我们以多分类任务为例来解释其基本原理：
                                        

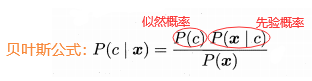
1. 最小错误率贝叶斯

                                
        最大后验分类规则： $c^{*}=argmax\left \{P(c_{i}|x)\right \}$

理解： 对于最大后验分类规则进行讲述，如下图所示，当 w_i 只有 w₁、w₂ 时：
                                
        已知 P( error | x），那么错误率则是：
                                                        
        最后得出最小错误率：
                                
        最大后验概率分类规则：选择后验概率最大的那一个w_i，此时错误率最小。

2. 极大似然估计

        
        令 D_c 表示训练集 D 中第 c 类样本组成的集合，假设这些样本是独立同分布的，则参数 θ_c 对于数据集 D_c 的似然是：
                                                        
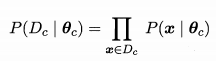
        对 θ_c 进行极大似然估计，就是去寻找能最大化似然 P(D_c I θ_c) 的参数值 $\hat{θ}_{c}$。 直观上看。 极大似然估计是试图在 θ_c 所有可能的取值中，找到一个能使数据出现的"可能性"最大的值。
                                                
                                                                
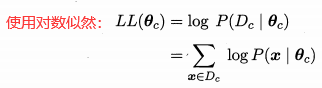
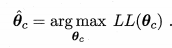
Eg: 用个例子来辅助理解：

3. 最小风险贝叶斯

        
        由于之前讲到了 最小错误率贝叶斯 等同于 最大后验概率规则。若引入损失函数，则比错误率更具一般性，并且允许有其他行为而不仅仅是判定类别，这时候提出了最小风险贝叶斯概念。

                                        
        假设正确判决损失为0，错误判决损失为1，且判决数目与类型数目相等，此时 最小风险判决规则 变为 最小错误率判决规则：
        
                                                                                         $\lambda _{ij}=\begin{cases} 0, & \text{if}\ i=j\ ; \\ 1, & \text{otherwise,} \\ \end{cases}$

        由上述两个式子可得： $R(c_{i}|x)=1\times P(c_{1}|x)+1\times P(c_{2}|x)+…+0\times P(c_{i}|x)+…+ 1\times P(c_{N}|x)$

        又因为 $\sum_{j=1}^{N}P(c_{j}|x)=1$，因此得到式子 :
                                                                                         $R(c|x)=1-P(c|x)$

                                                                                因此 R(c|x) min，则只需 P(c|x) max。

 
Eg: 用个例子来辅助理解：