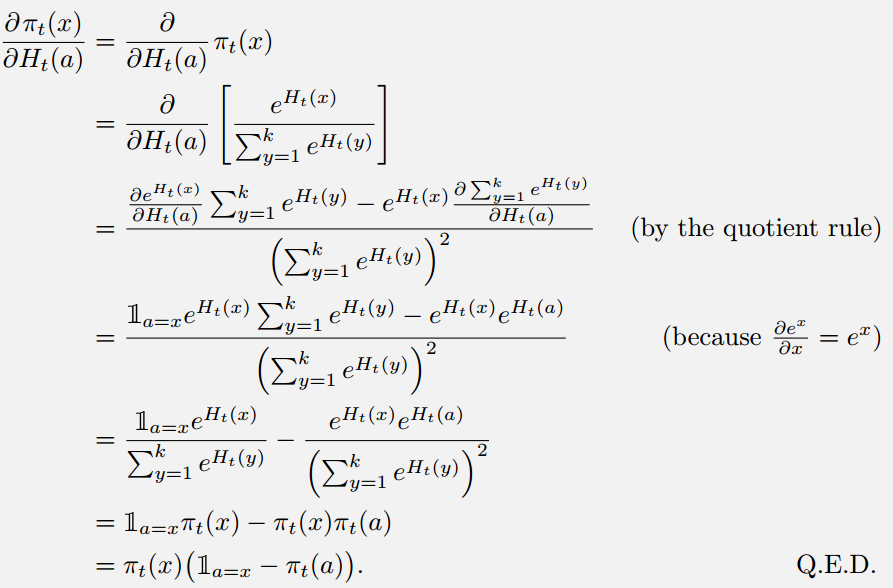文章目录

1.本章内容概要
2.k-臂赌博机问题
3.动作值方法
4.10臂赌博机实验
5.增量实现
6.非平稳情况的处理
7.保证探索 - 乐观初值方法
8.保证探索 - 基于上置信界的动作选择
9.梯度赌博机算法
10.多状态赌博机
11.总结
参考文献

1.本章内容概要

强化学习与其它学习相比，一个重要的特点是，强化学习利用训练信息(即根据环境信息设计的reward函数)评估我们采取的动作，而不是指导我们采取什么动作，这是RL需要探索的原因。评估性反馈(evaluative feedback, 也就是reward)表明我们当下采取的动作有多好，用来训练指示性反馈；指示性反馈(instructive feedback, 也就是value)指导算法采取哪个动作，不需要真的采取那个动作我们就能得到(通过value lookup table或者value approximator，对应表格型算法和拟合型算法，表格或者拟合器是根据交互的经验学习出来的[例如上一章Tic-Tac-Toe的状态值表]，后面章节详细介绍)。

这一章主要介绍单状态问题值函数的评估(利用evaluative feedback)，单状态问题是nonassociative的(策略不是状态的函数，因为只有一个状态)。注意上一章介绍的Tic-Tac-Toe问题是associative的，因为策略是状态(盘面)的函数。讨论这个简单情形可以避免完整的RL问题的复杂性，可以帮助我们更好地理解evaluative feedback与instructive feedback的区别和联系。

本章以多臂赌博机(老虎机)为例，介绍上述内容。

2.k-臂赌博机问题

赌博机问题可以描述为：假设有一台赌博机，上面有 k 个拉杆，每次拉下一个拉杆，就会获得一定的奖励。不同拉杆对应的奖励大小不一样(每个杆给出的奖励服从一个分布)。但是你提前并不知道哪个对应的奖励大。那么如果我们有N次拉杆机会，我们如何找到一个最优策略，使得获得的累计奖励最大？[1]

一个最直观的办法是：我们评估拉动每一个杆获得回报的期望值，当评估得比较准确后，选择期望最大的那个拉杆就好了。在时间t步，我们选择的动作(拉哪个杆，共k个可能)为 $A_t$ ，相应的回报是 $R_t$ 。对于某个动作a，我们定义它的值为(这个函数叫做动作值函数，衡量动作的好坏，这也就是instructive feedback，而 $R_t$ 是evaluative feedback)：

$q_*(a)=\mathbb{E}[R_t|A_t=a]$

我们只能利用有限的经验信息评估 $q_*(a)$ ，记时间t步的值估计为 $Q_t(a)$ 。我们只能根据 $Q_t(a)$ 来选择动作，如果我们每次都选择 $A_t=argmax_aQ_t(a)$ ，则我们的策略是贪婪(greedy)的(利用，exploiting)，但是如果我们开始就这么做，因为我们的估计太不准确了，导致 $A_t=argmax_aQ_t(a)$ 并不真的是最好的动作，因此我们不得不选择一些非最大 $Q_t(a)$ 的动作，从而得到关于各种动作的信息用来更好地评估 $q_*(a)$ (探索，exploring)。一般采用ε-greedy方法权衡exploiting和exploring，注意其实关于exploiting和exploring有很多更深入的研究，但是这些研究大多具有strong assumptions，因此不一定适用。

3.动作值方法

我们把先估计行为的值，然后基于行为值选择动作的方法称为行为值方法(action-value methods)。一个合理的估计是取经验中 $A_t=a$ 的奖励的均值：

$Q_t(a)\doteq\frac{\Sigma^{t-1}_{i=1}R_i\cdot\mathbb{1}_{A_i=a}}{\Sigma^{t-1}_{i=1}\mathbb{1}_{A_i=a}}$

注意，如果分母是0，则我们直接令 $Q_t(a)=0$ 即可。这个式子很直观，不需要详细解释。

得到了估计的行为值，我们以什么样的原则选择动作呢？上一个小节已经提到了，即取值最大的那个动作就行了(注意最大值如果出现在多个动作上，则从中随机选择)：
$A_t=argmax_aQ_t(a)$

为了保证探索性，采用ε-greedy策略：每次选择动作，以一个小概率 $\epsilon<1$ 随机选择一个动作，而不是总按照最大原则。ε-greedy可以保证所有的 $Q_t(a)$ 收敛到 $q_*(a)$ 。选择最优动作的概率可以随着时间推进而逐渐提高，或者说ε逐渐降低。

4.10臂赌博机实验

这个小节的目的是展示探索的作用。

10臂赌博机问题，共有10个动作，每个动作a都对应一个确定的奖励分布，每次该动作的奖励是从其对应分布上的采样。这里首先从一个正态分布 $N(0, 1)$ 上采样得到10个值，作为10个动作奖励分布的均值，也就是10个 $q_*(a)$ ，设置每个动作服从正态分布 $N(q_*(a), 1)$ 。

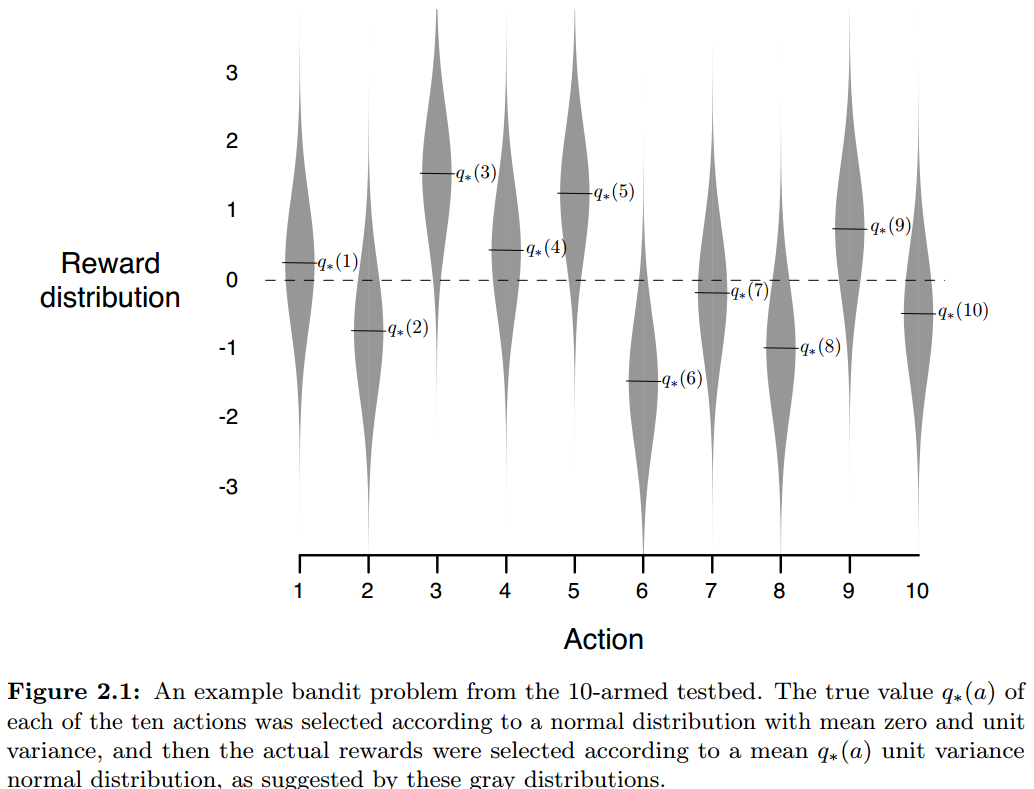
为了充分衡量算法的效果，我们按照上面介绍的步骤，生成2000个10臂赌博机问题，每个仿真1000个step，用这2000个问题上的平均值考量算法效果。下面给出选择不同ε时的收敛曲线( $ε=0$ 表示不探索)。

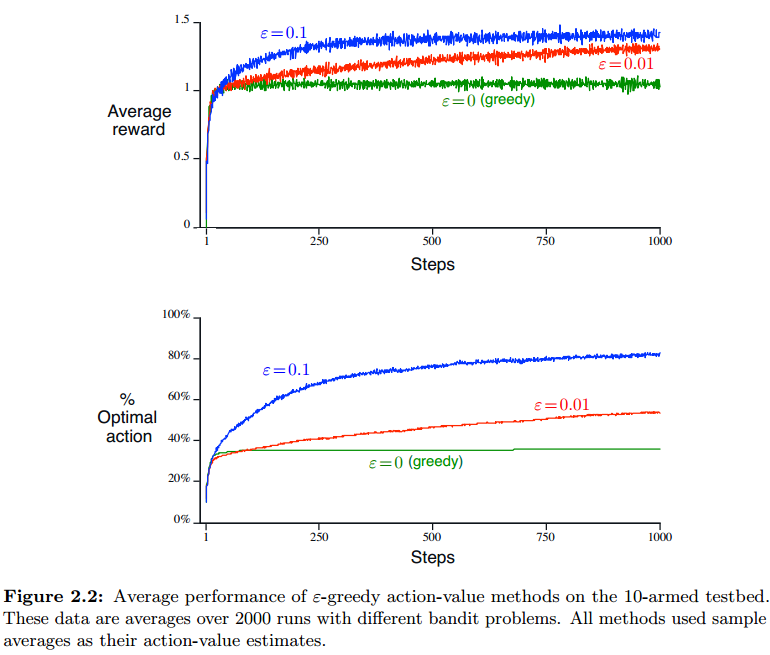
可以看出，ε小一些，会导致收敛变慢，但是会最终收敛到更好的解上去；实际上可以让ε从大到小变化。但是如果ε=0，则很难收敛到好的解。注意，这个问题是可以通过分析找到最大average reward的，大概在1.55左右:

$BestAverageReward = \mathbb{E} \left[max(q_*(A_1), ..., q_*(A_{10})) \right], q_*(A_i)\sim N(0, 1)$

如果问题reward的方差放大，则探索率应该适当高一些；如果问题是非平稳的(nonstationary，也就是在1000个step中，每个step上10个动作奖励的概率分布都会缓慢变化)，则探索也是非常必要的，生活中绝大部分问题都是nonstationary的。程序可以参考Github仓库。

5.增量实现

前面介绍的方法存在一个大问题，就是在计算 $Q_t(a)$ 时，我们需要利用所有的历史数据。这导致我们不得不存储所有的历史数据来估计 $q_*(a)$ ，使得存储量和计算量随着估计推进快速增加，这需要想办法克服，可以设计一个增量式的更新方法(此处公式先截图了…)。

我们考虑某动作a，用 $R_i$ 表示第i次选择该动作时的奖励值， $Q_n$ 表示对 $q_*$ 的第n次估计：

这样，我们只需要记录 $Q_n和n$ 就行了，计算量也非常小(想想递推最小二乘、kalman滤波，有木有觉得这个式子非常像)。式子中， $R_n-Q_n$ 叫估计误差(error in the estimate)，通过向目标走一小步来降低； $\frac{1}{n}$ 是更新步长(step-size)。

伪代码：

6.非平稳情况的处理

对于非平稳情况(每个动作奖励的概率分布是变化的)，需要给最近的样本更大的权重，较好的方法是使用固定的步长(constant step-size)，也就是把上小节的 $\frac{1}{n}$ 换成固定的步长α<1，原因是：

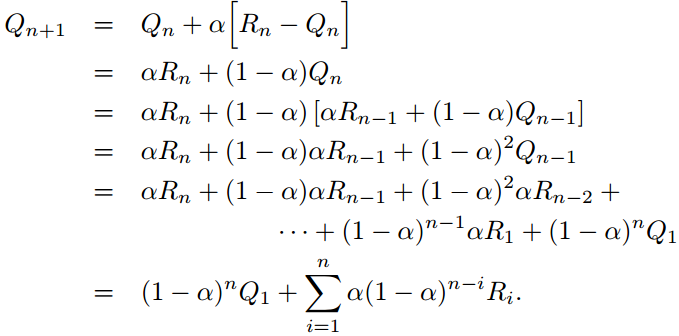
可以看到，固定步长相当于越最近的样本占的权重越大；而且所有系数之和恰好为1，我们把这叫做指数加权平均。下面我们分析下收敛条件。

首先考虑更一般的情况，我们用 $\alpha_n(a)$ 表示更新步长，这是一个随着n变化的序列，则只有序列 $\{\alpha_n(a)\}$ 满足如下条件时，增量更新公式才是收敛的：

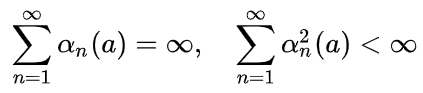
第一个条件保证能克服初值的误差和各种随机扰动；第二个条件保证了最终的收敛。如果取1/n，则所得结果为算术平均(样本均值sample-average)，这是能保证收敛的；但是constant step-size是不能保证收敛的，而是不断改变以适应最近得到的回报，但是对于nonstationary问题是必要的。注意大多数强化学习都是nonstationary的。因此，满足收敛条件的step-size序列往往用于理论分析而不是实际应用。

延伸一下，kalman滤波中，由于模型失真而产生的滤波器发散问题，可以通过加大最近数据的权重改善，叫做衰减记忆kalman滤波，本节的内容与之非常相似；还应该注意，上一章介绍的Tic-Tac-Toe并不是nonstationary的，它只是发生了状态的切换，是类似于associative的(切换与动作选择相关，因此不是完全associative的)。

7.保证探索 - 乐观初值方法

我们再观察下constant step-size更新公式：

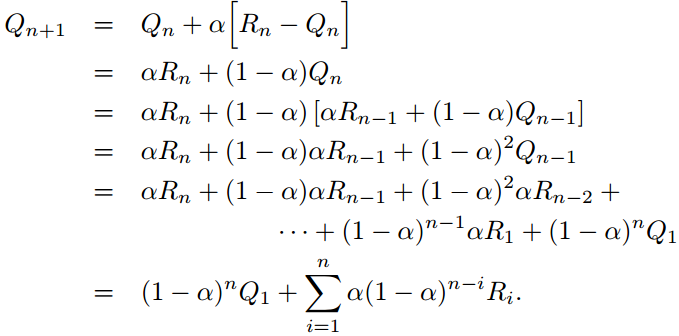
可见，估计是受到初值 $Q_1$ 影响的，而 $Q_1$ 只能由我们的经验设定，因此实际上估计是有偏的(但是渐进无偏)。合理选择初值，有助于算法找到更好的解。对于采样均值(sample-average)方法，这种偏差会随着每个动作被选择次数的增加而消失。对于常数步长方法来说，这种偏差则消失得慢很多。但是，这种需要提前设定的初值有时候是有利的，我们可以通过初始值来引入一些先验知识。

这里介绍的做法很简单，叫做optimistic initial values，也就是设置 $Q_1(a)$ 时，选个大一些的数，保证收敛到真值的过程实际上是个下降收敛的过程。这理解起来很直观，如果最初所有动作的值都一致，则我们会随机选一个动作执行并更新，更新后该动作的值下降；然后下次选择时，根据最大值原则，这个动作就不会被选中了，则剩余动作被随机选择一个，依此类推…这样，就相当于把利用和探索融合了起来。

注意到，optimistic initial values方法最开始收敛速度较慢，但是最终会比ε-greedy取得更好的效果。但是必须注意，这种方法只对平稳过程有效，对于nonstationary问题是基本无效的，因为即使收敛到暂时的真实值，一旦真实值上浮，则探索效果就消失了。

那个尖峰可能是因为最优动作由于真实值比较大，导致开始的误差小一些，因此修正比较小，这样进行一些更新后，这个最优动作就会比其它动作的值稍微大一些，导致经常被选中，从而出现尖峰；而当最优动作的误差值降低到与其它动作类似的时候，就不再有优势了。

8.保证探索 - 基于上置信界的动作选择

与ε-greedy和optimistic initial values类似，这是另一种平衡探索和利用的方式。但是UCB方法在探索时，综合考虑了估值的准确程度以及动作本身的好坏(值的大小)，理论上比ε-greedy效果更好。

UCB选择动作的公式为：

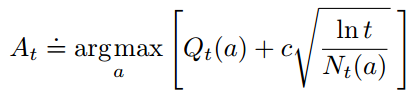
平方根项表示动作的值的估计方差， $N_t(a)$ 表示动作a被选择过的次数，c用来控制对探索与利用的权重，综合起来表示对于行为 a 值估计的不确定性度量；而第一项 $Q_t(a)$ 表示对动作好坏的度量。如果 $N_t(a)=0$ ，则认为这个动作的UCB是最大的，如果多个动作的UCB一样都是最大的，则从中随机选择一个。

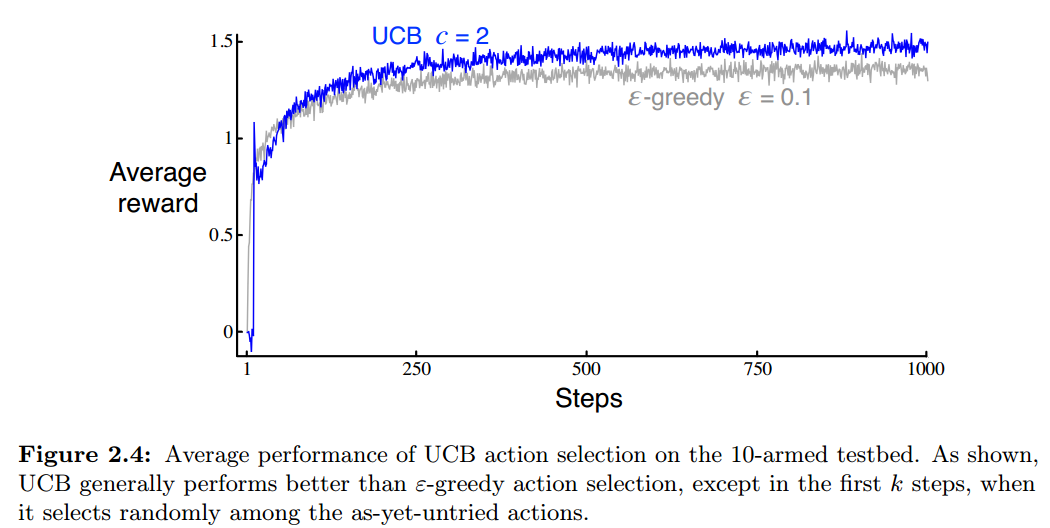
在时间t，某个动作的UCB与其Q值正相关，与其曾被选择的次数负相关，实际选择的动作是权衡这两者的；随着时间增长，由于UCB不确定度项中对时间取了对数，导致分子增长越来越慢，而分母的增长速度还是基本不变的，这导致不确定度项的数值逐渐下降，表示我们对值的估计越来越准确了。

根据试验结果，可以看到UCB是比ε-greedy好的。但是UCB不适用非平稳问题，实现也更复杂一些，还会因状态空间的扩大导致难以处理，因此实际场景中很难应用。

9.梯度赌博机算法

上面介绍的方法都是基于值函数的，这里我们考虑基于动作优势的方法，这种方法是RL中策略梯度(DPG、Actor-Critic等)方法的基础。我们用 $H_t(a)$ 表示动作a的偏好值。

一个直观的方法是比较所有动作a偏好的相对大小，我们可以用softmax函数(也叫Gibbs或Boltzmann分布)归一化(用 $\pi$ 表示某个策略，实际上是选择动作的概率)：

偏好函数的更新公式为：

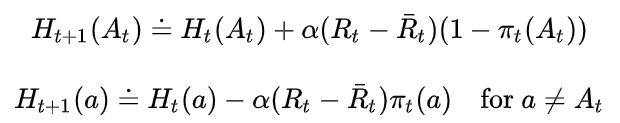
$\bar{R}_t$ 是 t 时刻之前所有回报的均值，它是比较reward的baseline，baseline是必须的，否则性能会大幅下降，尤其是在reward分布本身就不是0均值的时候。第一个式子是对被选中动作的更新，第二个式子是对未被选中动作的更新。

proof
根据梯度上升方法，我们考虑更新公式为(基础的梯度下降法，不解释了)：
$H_{t+1}(a) \doteq H_t(a) +\alpha\frac{\partial \mathbb{E}[R_t]}{\partial H_t(a)}$
下面证明，偏好函数的更新公式取期望时与梯度上升法是等价的。
将 $\mathbb{E}[R_t] = \sum_x \pi_t(x) q_*(x)$ 带入梯度上升公式，有：
$\begin{aligned} \frac{\partial \mathbb{E}[R_t]}{\partial H_t(a)} =& \frac{\partial}{\partial H_t(a)} \left[ \sum_x \pi_t(x) q_*(x)\right] \\ =& \sum_x q_*(x) \frac{\partial \pi_t(x)}{\partial H_t(a)} \\ =& \sum_x (q_*(x) - B_t) \frac{\partial \pi_t(x)}{\partial H_t(a)} \end{aligned}$
其中 $B_t$ 是不依赖x的baseline项，能添加这项是因为：
$\sum_x B_t \frac{\partial \pi_t(x)}{\partial H_t(a)} = B_t \sum_x \frac{\partial \pi_t(x)}{\partial H_t(a)} = B_t \frac{\partial[ \sum_x \pi_t(x)]}{\partial H_t(a)} = B_t \frac{\partial [1]}{\partial H_t(a)} = 0$
从而有( $B_t$ 替换为 $\bar{R}_t$ 是很自然的，而由于 $\mathbb{E}\left[ R_t | A_t \right] = q_*(A_t)$ ，因此 $q_*(A_t)$ 也可以替换)：
$\begin{aligned} \frac{\partial \mathbb{E}[R_t]}{\partial H_t(a)} =& \sum_x \pi_t(x)(q_*(x) - B_t) \frac{\partial \pi_t(x)}{\partial H_t(a)} / \pi_t(x) \\ =& \mathbb{E} \left[ (q_*(A_t) - B_t) \frac{\partial \pi_t(A_t)}{\partial H_t(a)} / \pi_t(A_t) \right] \\ =& \mathbb{E} \left[ (R_t - \bar{R}_t) \frac{\partial \pi_t(A_t)}{\partial H_t(a)} / \pi_t(A_t) \right] \end{aligned}$
由于：

于是：
$\begin{aligned} \frac{\partial \mathbb{E}[R_t]}{\partial H_t(a)} =& \mathbb{E} \left[ (R_t - \bar{R}_t) \pi_t(A_t)(\mathbb{1}_{a=A_t}-\pi_t(a)) / \pi_t(A_t) \right] \\ =& \mathbb{E} \left[ (R_t - \bar{R}_t)(\mathbb{1}_{a=A_t}-\pi_t(a))\right] \end{aligned}$
改成增量形式：
$H_{t+1}(a)=H_{t}(a)+\alpha(R_t-\bar{R}_t)(\mathbb{1}_{a=A_t}-\pi_t(a))$
需要强调的是，随机梯度上升对baseline是没有要求的，因此 $B_t$ 无论如何选择都满足梯度上升过程，baseline的选择不影响更新值的期望，但是会影响更新值的方差。

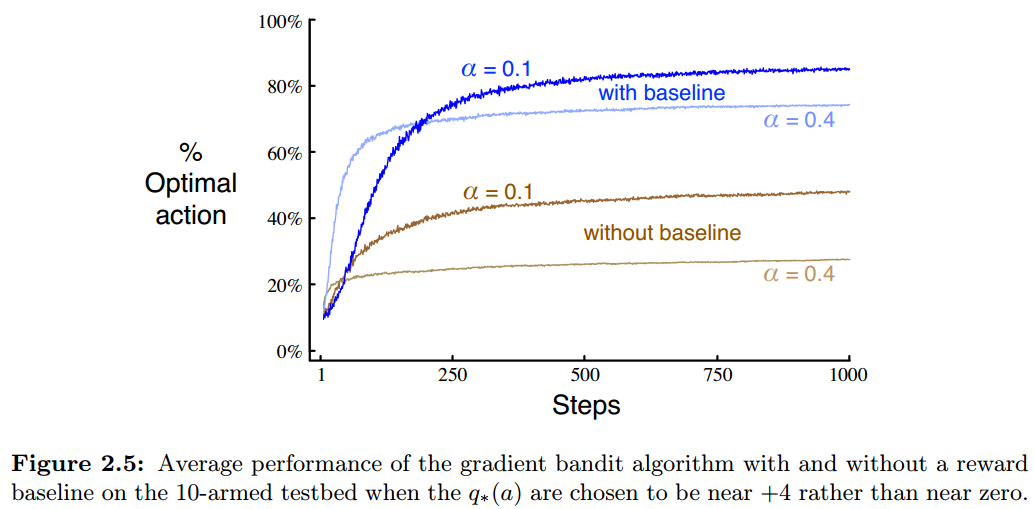
可见效果不错，也能看到baseline的巨大作用。baseline可以理解为，选择这个动作回报比过去的平均回报大，证明这个动作不错，增加偏好，相应地其它动作就降低偏好；反而反之。

10.多状态赌博机

上面讨论的都是nonassociative的，也就是赌博机每个摇臂对应的奖励分布在1000个steps中是不变的。如果这个分布是变化的(较剧烈，区别于nonstationary)，则问题就是associative的。我们可以认为最开始赌博机各个摇臂对应的分布构成一个状态s，然后下一个step变成了状态s’(分布变化了)，这里的状态转移与采取的动作 $A_t$ 没有关系，因此是介于k-armed bandit和完全RL的问题(完全RL状态转移与采取的动作相关)。

举个例子：我们初始化100组摇臂的分布(每组包含10个摇臂的均值和方差)，每个step我们随机选择其中的一组参数，根据这组参数采样出回报。这就构成了associative问题。

这nonstationary不同，nonstationary本质上只有一个状态s，但是这个状态随着时间缓慢连续变化；而associative具有多个状态，不同的step是在这多个状态之间切换，因此后者比前者变化剧烈很多，本章讨论的适用于nonstationary的方法无法用到associative上。

解决associative问题，一般我们需要一些clue，通过clue区别不同的状态，如果没有能区别状态的信号，那问题是无法解决的。

11.总结

本章的开始我们以多臂赌博机问题为例，介绍了最基本的行为值方法。为了平衡探索和利用问题，引入了ε-greedy策略和UCB策略。UCB在探索的时候能够考虑到每个行为的确定性，不确定性越大被访问的概率就越高。另外一个简单的trick就是设置一个比较理想的初始值函数，有时候它带来的探索效果可能比ε-greedy策略更好。最后我们还介绍了基于偏好选择行为的随机梯度上升法[2]。

各方法中都包含了超参数，例如ε-greedy中的ε、UCB中的c、梯度方法中的 $\alpha$ 、最优初值方法中的初值 $Q_0$ 。我们对这些参数选取多种值，各自进行多次试验，得到learning curve:

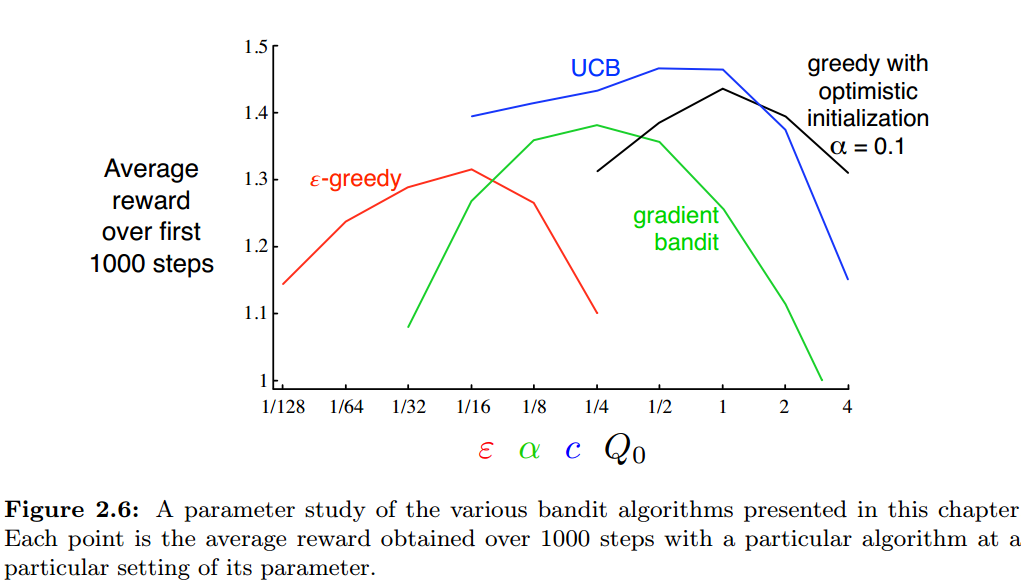
所有算法都是在参数居中时效果最好，而且在最好点附近，它们都对参数不是特别敏感(至少1个数量级)，UCB看起来表现是最好的。作者说，由于本文的方法都很简洁，且可以适用于各种RL任务，因此可以认为是state-of-the-art的，而那些复杂且精致的方法往往因为前提条件太难满足，无法得到实际应用。

对于k-armed bandit问题，用Gittins index(基于贝叶斯方法，根据先验选择最好动作，然后计算后验作为下一个step的先验，常采用posterior sampling or Thompson sampling处理分布)计算值函数是最好的探索和利用的权衡，但是要求分布已知且计算量较大，因此很难扩展。它和本章中distribution-free方法中最好情况是差不多的。在贝叶斯方法中，对每个动作先验分布，如果知道每个动作导致的reward分布，就可以计算后验了。但对于离散问题，树状结构指数级扩大，导致开销不能接受。但是或许这能用估计的方法逼近，把bandit方法转换为标准RL问题，感兴趣可以参考Bibliographical and Historical Remarks提到的文献。