Buge's Fibonacci Number Problem

题意：

数据范围：

Each test case contains 7 integers, they are f1, f2, a, b, k, n, m which were just mentioned above, where 0 < f1, f2, a, b, n, m < 1000 000 000, and 0 ≤ k < 50.

题解：对于这种k次方，而且累加求和的一般都是矩阵快速幂，只要是构造矩阵比较麻烦。

看一个大神的题解（侵删）：

本题要二项式展开，别怕麻烦。

扫描二维码关注公众号，回复： 999964 查看本文章

方法和以前的矩阵推法一样，就是矩阵是变化的，根据数据而变化。

先自己写下，感觉纸写不下时，就别写了！

设k=3;自己展开算一下：

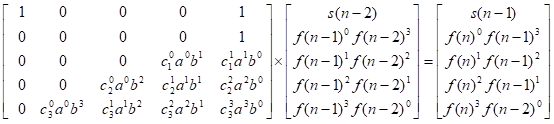
右边的展开：就是用f(n)=af(n-1)+bf(n-2) 把f(n)都换成 f(n-1)f(n-2)的表达式，最后根据表达式把上面左边的矩阵求出。惊奇的发现很有规律，是个下三角矩阵，和k有直接的关系。

是k+2的方阵。设该方阵为A，则 (A*F). a11=s(2);所以只要计算 n-1次，就能算出s(n)了。

注意：s(1)不等于f1, s(1)=f1^k,我在这里WA 了20次，低级错误！

所以当k>3时，矩阵也推出来了。

就是二项式的展开作为系数的下三角矩阵。

如何解决矩阵的大小不固定问题：

想了很多，想用类，或用指针，走了弯路！

突然想到，初始化开1个很大的2维数组，然后每次矩阵乘法时根据每组数据的矩阵的维数来计算就行了，实际运行时正确的，测试很多回了，基本没改动模板，看代码就懂了。

#include <iostream>
#include <stdio.h>
#include <string.h>
#define LL long long

using namespace std;

const int maxn=50;
LL mod,k,K;
struct Mat
{
    LL mp[maxn+10][maxn+10];
} res,A;

LL C[maxn+10][maxn+10];
LL line[maxn+10];

void get_C()
{
    C[0][0]=1;
    for(int i=1; i<=maxn; ++i)
    {
        C[i][0]=1;
        for(int j=1; j<=i; ++j)
            C[i][j]=(C[i-1][j]+C[i-1][j-1]);
    }
}

LL _pow(LL x,LL y)
{
    LL ans=1;
    while(y>0)
    {
        if(y&1) ans=ans*x%mod;
        x=x*x%mod;
        y/=2;
    }
    return ans;
}

Mat Mul(Mat a,Mat b)
{
    Mat c;
    memset(c.mp,0,sizeof(c.mp));
    for(LL kk=0; kk<k; ++kk)
        for(LL i=0; i<k; ++i)
        {
            if(a.mp[i][kk]==0) continue;
            for(LL j=0; j<k; ++j)
                c.mp[i][j]=(c.mp[i][j]+(a.mp[i][kk]*b.mp[kk][j]%mod))%mod;

        }
    return c;
}

LL Cal(LL y)
{
    while(y>0)
    {
        if(y&1) res=Mul(res,A);
        y/=2;
        A=Mul(A,A);
    }

    LL ans=0;
    for(LL i=0; i<k; ++i)
    {
        ans=(ans+res.mp[0][i]%mod*line[i]%mod)%mod;
    }
    return ans;
}

int main()
{
    get_C();

    LL f1,f2,a,b,n;
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%lld %lld %lld %lld %lld %lld %lld",&f1,&f2,&a,&b,&k,&n,&mod);
        K=k;
        k=k+2;
        memset(res.mp,0,sizeof(res.mp));
        for(LL i=0; i<k; ++i)
            res.mp[i][i]=1;
        memset(A.mp,0,sizeof(A.mp));
        A.mp[0][0]=A.mp[0][k-1]=1;

        int r=0,l;
        for(LL i=1; i<k; ++i)
        {
            l=0;
            for(LL j=k-i; j<k; ++j)
            {
                A.mp[i][j]=(C[r][l]%mod*_pow(a,l)%mod*_pow(b,r-l))%mod;
                l++;
            }
            r++;
        }

        line[0]=_pow(f1,K)%mod;
        l=0;
        for(LL i=1; i<k; ++i)
        {
            line[i]=_pow(f2,l)%mod*_pow(f1,K-l)%mod;
            l++;
        }

        printf("%lld\n",Cal(1ll*(n-1)));
    }
    return 0;
}

具体的文件传在网上了链接：http://pan.baidu.com/s/1slJk169 密码：38j8

不定维数矩阵构造 - hdu3509

Buge's Fibonacci Number Problem

猜你喜欢