5 操作臂动力学

1.绪论

前面几章主要介绍了机器人的运动学，逆运动学以及机器人关节广义速度，本章开始介绍机器人的动力学模型。机器人动力学模型一般由一个二阶非线性微分方程组表示，通常十分复杂，含有强非线性、强耦合等。一般有两种建立动力学模型的方法:牛顿-欧拉方法，以及拉格朗日方法。本章这里只介绍拉格朗日方法。

2.操作臂动力学的拉格朗日公式

定义拉格朗日函数 $L$ ：

$L=K-P$ K:系统运动部分的总动能，P:系统的总势能

系统的动力学方程（拉格朗日-欧拉（L-E）方程）：

$\frac{d}{dt}\left [\frac{\partial L}{\partial \dot{q}_{i}} \right ]-\frac{\partial L}{\partial q_{i}}=\tau _{i},i=1,2,...,n$

$q_i$ -----第i关节的广义变量

$\dot{q_i}$ ------第i关节的广义速度

$\tau_{i}$ ------作用于第i连杆的外部广义力（视 $q_i$ 为转/平动分为力矩/力）

假设各连杆的动能为 $K_i$ ,势能为 $P_i$ ，则总动能和总势能为：

$K=\sum_{i=1}^{n}K_i,P=\sum_{i=1}^{n}P_i$

因为势能 $P$ 仅是位置 $q$ 的函数 $P(q)$ ，所以L-E方程可以简化为：

$\frac{d}{dt}\left[\frac{\partial K}{\partial \dot{q}_{i}}\right]-\frac{\partial K}{\partial {q}_{i}}+\frac{\partial P}{\partial {q}_{i}}=\tau_i,i=1,2,...,n$

或者矢量表达形式：

$\frac{d}{dt}\left[\frac{\partial K}{\partial \dot{q}}\right]-\frac{\partial K}{\partial {q}}+\frac{\partial P}{\partial {q}}=\tau$

举一个简单的实例：

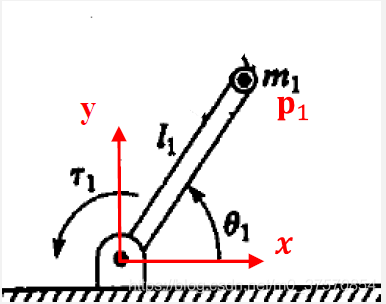
驱动单杆转动，杆质量集中在端点，平面上设立参考系。

1、计算杆质量点的位置 $p_1$ :

$p_1=\begin{bmatrix} L_1c_1\\L_1s_1 \end{bmatrix}$

2、计算质量点的速度向量 $\dot{p_1}$ :

$\dot{p_1}=\begin{bmatrix} -L_1s_1\\L_1c_1 \end{bmatrix}\dot{\theta_{1}}$

3、计算质量点的速度：

$\left \| \dot{p}_{1} \right \|=\left | L_1\dot{\theta}_{1} \right |$

4、计算杆1的动能 $K_1:$

$K_1=\frac{1}{2}m_1\left \| \dot{p}_{1}^{2} \right \|=\frac{1}{2}m_1L_{1}^{2}\dot{\theta}_{1}^{2}$

5、计算杆1 的重力势能 $P_1$ ：

$P_1=-m_1[0 -g]p_1=m_1gL_1s_1$

6、拉格朗日函数 $L$ :

$L=K_1-P_1=\frac{1}{2}m_1L_{1}^{2}\dot{\theta}_{1}^{2}-m_1gL_1s_1$

7、计算 $\frac{\partial L}{\partial \dot{\theta}_1}$ :

$\frac{\partial L}{\partial \dot{\theta}_1}=m_1L_1^{2}\dot{\theta}_1$

8、计算 $\frac{d}{dt}\frac{\partial L}{{\partial} \dot{\theta}_1}$

$\frac{d}{dt}\frac{\partial L}{{\partial} \dot{\theta}_1}=m_1L_1^{2}\ddot{\theta}_1$

9、计算 $\frac{\partial L}{\partial {\theta}_1}$ ：

$\frac{\partial L}{\partial {\theta}_1}=-m_1gL_1c_1$

10、由拉格朗日-欧拉方程：

$\frac{d}{dt}\left [ \frac{\partial L}{\partial \dot{q}_{1}} \right ]-\frac{\partial L}{\partial q_1}=\tau_1$

代入得到动力学模型：

$m_1L_{1}^{2}\ddot{\theta}_{1}+m_1gL_1c_1=\tau_1$

3.动力学方程推导过程

——计算任一连杆上任一点的速度

——计算各连杆的的动能和机器人系统的总动能

——计算各连杆的势能和机器人系统的总势能，得到拉格朗日函数L

——对拉格朗日函数求导，得到动力学方程式

1）计算任一连杆上任一点的速度

连杆 $i$ 上任一点 $^{i}r$ 在基座标系下的位置为 $r={_{0}^{i}T}\cdot {^{i}r}$ ，该点的速度为：

$v=\frac{dr}{dt}={^{0}_{i}\dot{T}}\cdot{^{i}r}=\left [ \sum_{j=1}^{i}\frac{\partial _{0}^{i}\dot{T}}{\partial q_j}\dot{q_j} \right ]\cdot{^{i}r}$

速度的内积 $\left \| v \right \|^2=v^{T}v=v_x^2+v_y^2+v_z^2$

$v^Tv=Trace\left[\sum_{j=1}^{i}\sum_{k=1}^{i}\frac{\partial _{i}^{0}T}{\partial q_j} {^{i}r}{^{i}r^{T}}\left[\frac{\partial _{i}^{0}T}{\partial q_k} \right ]^{T}\dot{q_j}\dot{q_k}\right ]$

2）计算各连杆的动能和机器人系统总动能

设连杆 $i$ 上任一点的质量为 $dm$ ，其动能为：

$dK_{i}=\frac{1}{2}v^{T}v\cdot dm=\frac{1}{2}Trace\left[\sum_{j=1}^{i}\sum_{k=1}^{i}\frac{\partial _{i}^{0}T}{\partial q_j} {(^{i}r}{^{i}r^{T} dm)}\left[\frac{\partial _{i}^{0}T}{\partial q_k} \right ]^{T}\dot{q_j}\dot{q_k}\right ]$

对连杆 $i$ 进行积分，得到连杆 $i$ 的动能：

$K_{i}=\int_{rod}dK_{i}=\frac{1}{2}Trace\left[\sum_{j=1}^{i}\sum_{k=1}^{i}\frac{\partial _{i}^{0}T}{\partial q_j} {(\int_{rod }{^{i}r}{^{i}r^{T} dm})}\left[\frac{\partial _{i}^{0}T}{\partial q_k} \right ]^{T}\dot{q_j}\dot{q_k}\right ]$

在这里记“伪惯量阵”为：

$I_i=\int_{rod} {^{i}r ^{i}r^{T}dm}=\left[\begin{matrix} \int {^{i}x^{2}dm} & \int {^{i}x^{i}ydm} & \int {^{i}x^{i}zdm} &\int {^{i}xdm} \\ \int {^{i}y^{i}xdm} & \int {^{i}y^{2}dm} & \int {^{i}y^{i}zdm} &\int {^{i}ydm} \\ \int {^{i}z^{i}xdm} & \int {^{i}z^{i}ydm} & \int {^{i}z^{2}dm} &\int {^{i}zdm} \\ \int {^{i}xdm} & \int {^{i}ydm} & \int {^{i}zdm} &\int dm} \end{matrix} \right ]$

其中， $^{i}r=\begin{bmatrix} ^{i}x & ^{i}y & ^{i}z & 1 \end{bmatrix}^{T}$

注意到：

$\int_{rod (i)}$ 等于连杆i的质量 $m_i$ ：

$\int_{rod (i)}{^{i}xdm},\int_{rod (i)}{^{i}ydm},\int_{rod (i)}{^{i}zdm}$ 分别是连杆 $i$ 的质心位置坐标 $^{i}\bar{x}_{i},^{i}\bar{y}_{i},^{i}\bar{z}_{i}$ 以及物体的转动惯量、协转动惯量分别为：

$I_{ixx}=\int_{rod(i)}(^{i}y_{i}^{2}+^{i}z_{i}^{2})dm$

$I_{iyy}=\int_{rod(i)}(^{i}x_{i}^{2}+^{i}z_{i}^{2})dm$

$I_{izz}=\int_{rod(i)}(^{i}y_{i}^{2}+^{i}x_{i}^{2})dm$

$I_{ixy}=I_{iyx}=\int_{rod(i)}{^{i}x^{i}y}dm$

$I_{ixz}=I_{izx}=\int_{rod(i)}{^{i}x^{i}z}dm$

$I_{iyz}=I_{izy}=\int_{rod(i)}{^{i}y^{i}z}dm$

有：

$I_{i}=\begin{bmatrix} \frac{-I_{ixx}+I_{iyy}+I_{izz}}{2} & I_{ixy} & I_{ixz} &m_{i}{^{i}\bar{x}_{i}} \\ I_{iyx}& \frac{I_{ixx}-I_{iyy}+I_{izz}}{2} & I_{iyz} &m_{i}{^{i}\bar{y}_{i}} \\ I_{izx}& I_{izy} & \frac{I_{ixx}+I_{iyy}-I_{izz}}{2} & m_{i}{^{i}\bar{z}_{i}}\\ m_{i}{^{i}\bar{x}_{i}}& m_{i}{^{i}\bar{y}_{i}} & m_{i}{^{i}\bar{z}_{i}} & m_i \end{bmatrix}$

此时连杆 $i$ 的动能可以写为：

$K_{i}=\int_{rod}dK_{i}=\frac{1}{2}\sum_{j=1}^{i}\sum_{k=1}^{i}Trace\left[\frac{\partial _{i}^{0}T}{\partial q_j} I_{i}\frac{\partial _{i}^{0}T}{\partial q_k} ^{T}\right ]\dot{q_j}\dot{q_k}$

假设不计连杆 $i$ 的传动装置动能，那么系统的总动能为：

$K=\sum_{i=1}^{n}K_{i}=\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{i}\sum_{k=1}^{i}Trace\left[\frac{\partial _{i}^{0}T}{\partial q_j} I_{i}\frac{\partial _{i}^{0}T}{\partial q_k} ^{T}\right ]\dot{q_j}\dot{q_k}$

3）计算各连杆位能和机器人系统总势能，以及拉格朗日函数

设连杆 $i$ 上任一点的质量为 $dm$ ,其势能为：

$dP_{i}=-dmg^{T}r=-g^{T}{^{0}_{i}T^{i}rdm},g=\begin{bmatrix} 0 &0 &-9.81 &0 \end{bmatrix}^{T}$

对连杆 $i$ 进行积分，得到连杆 $i$ 的位能：

$P_{i}=-\int_{rod(i)}g^{T}{^{0}_{i}T}{^{i}r}\cdot dm=-g^{T}{^{0}_{i}T}\int_{rod(i)}{^{i}r}\cdot dm=-m_{i}g^{T}{^{0}_{i}T}{^{i}\bar{r}_{i}}$

其中 ${^{i}\bar{r}_{i}}=\begin{bmatrix} {^{i}\bar{x}}& {^{i}\bar{y}} & {^{i}\bar{z}} & 1 \end{bmatrix}$

系统总的位能为：

$P=\sum_{i=1}^{n}=-\sum_{i=1}^{n}m_{i}g^{T}{^{0}_{i}T}^{i}\bar{r}_{i}$

系统的拉格朗日函数为：

$L=K-P=\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{i}\sum_{k=1}^{i}Trace\left[{\frac{\partial {^{0}_{i}T}}{\partial {q}_{j}}}I_{i} {\frac{\partial {^{0}_{i}T^{T}}}{\partial {q}_{j}}}\right ]\dot{q}_{j}\dot{q}_{k}-\sum_{i=1}^{n}m_{i}g^{T}{^{0}_{i}T}{^{i}\bar{r}_{i}}$

4)对拉格朗日函数求导，得到动力学方程式。

首先将拉格朗日函数对 $\dot{q_{p}}$ 求导：

$\frac{\partial L}{\partial {\dot{q}_{p}}}=\frac{1}{2}\sum_{i=1}^{n}\left[\sum_{k=1}^{i}Trace\left[{\frac{\partial {^{0}_{i}T}}{\partial {q}_{p}}}I_{i} {\frac{\partial {^{0}_{i}T^{T}}}{\partial {q}_{k}}}\right ]\dot{q}_{k} +\sum_{j=1}^{i}Trace\left[{\frac{\partial {^{0}_{i}T}}{\partial {q}_{j}}}I_{i} {\frac{\partial {^{0}_{i}T^{T}}}{\partial {q}_{p}}}\right ]\dot{q}_{j}\right ]$

$=\sum_{i=1}^{n}\sum_{k=1}^{i}Trace\left[{\frac{\partial {^{0}_{i}T}}{\partial {q}_{k}}}I_{i} {\frac{\partial {^{0}_{i}T^{T}}}{\partial {q}_{p}}}\right ]\dot{q}_{k}$

$=\sum_{i=p}^{n}\sum_{k=1}^{i}Trace\left[{\frac{\partial {^{0}_{i}T}}{\partial {q}_{k}}}I_{i} {\frac{\partial {^{0}_{i}T^{T}}}{\partial {q}_{p}}}\right ]\dot{q}_{k}$

因为： $\frac{d}{dt}\left[\frac{\partial{^{0}_{i}T}}{\partial q_j} \right ]=\sum_{k=1}^{i}\frac{\partial}{\partial q_j}\left[\frac{\partial ^{0}_{i}T}{\partial q_j} \right ]\dot{q}_k$

所以有：

$\frac{d}{dt}\frac{\partial L}{\partial {\dot{q}_{p}}}=\sum_{i=1}^{n}\sum_{k=1}^{i}Trace\left[ {\frac{\partial ^{0}_{i}T}{\partial q_k}}I_i{\frac{\partial ^{0}_{i}T^{T}}{\partial q_p}}\right ]\ddot{q}_{k}+\sum_{i=p}^{n}\sum_{j=1}^{i}\sum_{k=1}^{i}Trace\left[ {\frac{\partial^{2} {^{0}_{i}T}}{\partial q_j \partial{q_k}}}I_i{\frac{\partial ^{0}_{i}T^{T}}{\partial q_p}}\right ]\dot{q}_{j}\dot{q}_{k}+\sum_{i=p}^{n}\sum_{j=1}^{i}\sum_{k=1}^{i}Trace\left[ {\frac{\partial^{2} {^{0}_{i}T}}{\partial q_p \partial{q_k}}}I_i{\frac{\partial ^{0}_{i}T^{T}}{\partial q_j}}\right ]\dot{q}_{j}\dot{q}_{k}$

$=\sum_{i=1}^{n}\sum_{k=1}^{i}Trace\left[ {\frac{\partial ^{0}_{i}T}{\partial q_k}}I_i{\frac{\partial ^{0}_{i}T^{T}}{\partial q_p}}\right ]\ddot{q}_{k}+2\sum_{i=p}^{n}\sum_{j=1}^{i}\sum_{k=1}^{i}Trace\left[ {\frac{\partial^{2} {^{0}_{i}T}}{\partial q_j \partial{q_k}}}I_i{\frac{\partial ^{0}_{i}T^{T}}{\partial q_k}}\right ]\dot{q}_{j}\dot{q}_{k}$

$\frac{\partial L}{\partial q_p}=\frac{1}{2}\sum_{i=p}^{n}\sum_{j=1}^{i}\sum_{k=1}^{i}Trace\left[ {\frac{\partial^{2} {^{0}_{i}T}}{\partial q_j \partial{q_k}}}I_i{\frac{\partial ^{0}_{i}T^{T}}{\partial q_k}}\right ]\dot{q}_{j}\dot{q}_{k}+\frac{1}{2}\sum_{i=p}^{n}\sum_{j=1}^{i}\sum_{k=1}^{i}Trace\left[ {\frac{\partial^{2} {^{0}_{i}T}}{\partial q_k \partial{q_p}}}I_i{\frac{\partial ^{0}_{i}T^{T}}{\partial q_k}}\right ]\dot{q}_{j}\dot{q}_{k}+\sum_{i=p}^{n}m_{i}g^{T}\frac{\partial ^{0}_{i}T}{\partial q_p}{^{i}\bar{r}_{i}}$

$=\sum_{i=p}^{n}\sum_{j=1}^{i}\sum_{k=1}^{i}Trace\left[ {\frac{\partial^{2} {^{0}_{i}T}}{\partial q_k \partial{q_p}}}I_i{\frac{\partial ^{0}_{i}T^{T}}{\partial q_k}}\right ]\dot{q}_{j}\dot{q}_{k}+\sum_{i=p}^{n}m_{i}g^{T}\frac{\partial ^{0}_{i}T}{\partial q_p}{^{i}\bar{r}_{i}}$

写出全部拉格朗日方程：

$\frac{d}{dt}\left[\frac{{\partial L}}{\partial \dot{q}_{i}} \right ]-\frac{\partial L}{\partial \dot{q}_i}=\tau_{i},i=1,...,n$

$\sum_{j=1}^{n}D_{ij}\ddot{q}_{j}+\sum_{j=1}^{n}\sum_{k=1}^{n}D_{ijk}\dot{q}_{j}\dot_{q}_{k}+D_i=\tau_i,i=1,....n$

其中：

$D_{ij}=\sum_{p=max(i,j)}^{n}=Trace\left[ {\frac{\partial^{2} {^{0}_{p}T}}{\partial q_j }}I_p{\frac{\partial ^{0}_{p}T^{T}}{\partial q_i}}\right ],i,j=1,...,n$

$D_{ijk}=\sum_{p=max(i,j,k)}^{n}=Trace\left[ {\frac{\partial^{2} {^{0}_{p}T}}{\partial q_j \partial q_k}}I_p{\frac{\partial ^{0}_{p}T^{T}}{\partial q_i}}\right ],i,j,k=1,...,n$