0. 前言

又到了上课的时间，组合数学的书是《组合理论及其应用》，这次从二分图（第六章）开始讲起。这本书的二分图是从几何的角度进行讲述。这里有个题外话，组合数学的前序课程应该是《离散数学》，主要包括数理逻辑、集合论、代数和图论四个部分。

1. 相异代表系

1.1 定义

相异代表系是针对几何来讲的，这里主要抓住“相异”、“代表”、“系”三个部分来进行区分，首先是系表明是一个集合，代表则是集合内每一个元素代表着一个子集（即该元素来源于这个子集），相异表明其元素各不相同。下面给出其形式化定义：

例如： $A_1=\{1,4\},A_2=\{1,2,3\},A_3=\{3,4,5\},A_4=\{3,4,5\},$其一个代表系可以是：{1,1,3,3}（有元素相同），而一个相异代表系则可以是：{1,2,3,4}（每个元素都来自不同的子集，都不相同）。

1.2 集族有相异代表系的条件

非空集合构成的集族一定有代表系，但不一定有相异代表系。那么什么时候集族有相异代表系呢？1935年的何氏定理告诉了我们的充要条件。

这定义比较拗口，其大致意思就是若有n个子集，从中任意选取k个子集，其并集的元素个数≥k。这里有一个疑问，这定理有啥用啊，相异代表系好像仅仅是为了存在而存在啊？这个疑问我们先放一放，因为这个问题我们后面解释。

既然是数学，那么给出一个定理时，一个必要的操作就是要证明它。这是一个充要条件。必要性是必然的，因为互不相同的k个元素的并集一定是大于等于k的，下面主要证明充分性。

这里又有一个题外话：数学的证明方法有哪些？
需要证明和整数n有关，且n为无穷时，使用数学归纳法；
需要证明和整数n有关，且n是有限的，使用枚举法（分类讨论、分析法）
直接证明、间接证明都不太容易时，使用反证法。
如果要考虑最值、条件时，使用构造法。

这里使用数学归纳法进行证明：
当m=1时， $|A_1|\ge1$成立。
当m<n时，假设满足条件。
当m=n时，这里再使用分类讨论方法进行证明。
（1）对任意 $1\le k\le n-1$，任意选择 $1 \le i_1 \le i_2 \le i_3\le ... \le i_k \le n$，满足条件 $|\bigcup_{i=1}^{k} A_i|\ge k+1$（这个条件比定理上的要求更严格）此时，取 $e_n \in A_n$，使得 $|\bigcup_{i=1}^{k} A_i-\{e_n\}|\ge k$
则 $e_1,e_2,...,e_{n-1}$就是其（ $A_i-\{e_n\}$）相异代表系，从而使得 $e_1,e_2,...,e_{n-1},e_n$是其 $\{A_1,A_2,...,A_n\}$的相异代表系。

以上只是比较好证明的一部分，下面证明剩余的部分：

（2）对存在 $1\le p\le n-1$，存在某种选择 $1 \le i_1 \le i_2 \le i_3\le ... \le i_p\le n$，使得 $|A_1\cup A_2\cup ...\cup A_p|=p$，符合假设条件，有相异代表系 $F=\{e_1,e_2,...,e_p\}$（到这里都是在找一个前提条件）。

现在考虑剩余的n-p个集合构成的集族 $\{A_{p+1}-F, A_{p+2}-F,...,A_{p+n}-F\}$，对于任意 $1\le k\le n-p$有
$|(A_{j1}-F)\cup(A_{j2}-F)\cup ... \cup(A_{jk}-F)|$
$=|(A_{j1}\cup A_{j2}\cup ... \cup A_{jk})-F|$
$=|(A_{1}\cup A_{2}\cup ... \cup A_{p}\cup A_{j1}\cup A_{j2}\cup ... \cup A_{jk})-F|$
$\ge(p+k)-p=k$
满足定理原始条件，即 $\{A_{p+1}-F, A_{p+2}-F,...,A_{p+n}-F\}$有相异代表系 $\{e_{p+1},e_{p+2},...,e_{n}\}$，因此结合前提条件，就可以获得存在相异代表系 $\{e_1,e_2,...,e_n\}$。

综上（1）（2）证毕。

1.3 集族的子集存在相异代表系

如果集合E没有相异代表系，则最多可以有多少r元子集有相异代表系？下面这个定理告诉我们：

还是需要证明：
当 $1 \le k \le n-r$时，等式右边是负数，不等式自动满足。

这里证明分为两步走，首先令 $F=\{ f_1,f_2,...,f_{n-r}\}$,且 $F\cap (A_1 \cup A_2\cup ... \cup A_n)=\varnothing$
先证明（1）：{A_1,A_2,…,A_n}的r 元子集有相异代表系，当且仅当 $\{A_1 \cup F，A_2\cup F, ... ,A_n \cup F \}$有相异代表系。

先证明充分性。假设集族有r元子集相异代表系为 ${e_1,e_2,...,e_r}$，显然 ${e_1,e_2,...,e_r,f_1,f_2,...,f_{n-r}}$就是 $\{A_1 \cup F，A_2\cup F, ... ,A_n \cup F \}$的相异代表系。

再证明必要性。假设 $\{A_1 \cup F，A_2\cup F, ... ,A_n \cup F \}$有相异代表系 $x_1,x_2,...,x_n$,因为F中只有n-r个元素，所以 $x_1,x_2,...,x_n$中至少有r个元素不在F中，因此 $x_1,x_2,...,x_r$是 $\{A_1，A_2, ... ,A_n \}$的一个相异代表系。

然后证明（2）：定理6.1.2。

根据定理6.1.1, $\{A_1 \cup F，A_2\cup F, ... ,A_n \cup F \}$有相异代表系,且
$|(A_1 \cup F) \cup (A_2 \cup F) \cup ... \cup(A_k \cup F)|\ge k$
从而
$|(A_1 \cup F) \cup (A_2 \cup F) \cup ... \cup(A_k \cup F)|$
$=|A_1 \cup A_2 \cup ... \cup A_k \cup F |$
$=|A_1 \cup A_2 \cup ... \cup A_k|+ | F |$
从而
$=|A_1 \cup A_2 \cup ... \cup A_k|\ge k-(n-r)$
也就是
$=|A_1 \cup A_2 \cup ... \cup A_k|+(n-k）\ge r$

因此，可以有以下推论：

这个意思就是说，要使得选取的集合数最多，而其并集的个数最小。

2. 二分图

2.1 二分图的定义

如果一个图的节点的集合V可以分为2个部分，分别是X和Y，且 $V=X \cup Y, X \cap Y=\empty$,且其边均为[x,y]其中 $x \in X, y \in Y$,则该图为二分图。也就是说该图的节点两个部分，所有的边都在这两个部分之间，各部分之内没有边，如图所示：

这是一个非常特殊的图结构，具有很多特性。等等，既然二分图的定义这么简单，那为啥第一章还要介绍相异代表系呢？

2.2 二分图的匹配

上图的一个用处就是描述“婚姻匹配”问题，（左边都是女生，右边都是男生，毕竟女生比男生少嘛），那这样就是否存在一个匹配，使得女生都有归宿。如果存在这样一个匹配，就可以使用相异代表系表示。例如上图可以表示为集族： $A_1=\{y_1, y_2 \},A_2=\{y_1, y_3 \},A_3=\{y_2, y_3, y_4 \},A_4=\{y_4, y_5 \}$,则 $\{[1,y_1],[2,y_3],[3,y_4],[4,y_5]\}$没有公共节点，因此是该图的一个匹配。（也是其集族的相异代表系）。

因此这个二分图和相异代表系的关系如下：

2.3 二分图的覆盖

刚才是从边出发，给定结点的约束条件，从而形成匹配的概念。与之相反的，二分图的覆盖则从点出发，给定边的约束条件：
如果结点集合S $\subseteq X \cup Y$,使得边集合 $\triangle$每条边至少有一个结点在其中，则称S为 $\triangle$的一个覆盖。
例如，上图中 $\{1,2，3,4\}，\{3,4，y_1，y_2，y_3\}$都是 $\triangle$的覆盖

2.4 匹配与覆盖的关系

就像上面的两个定义一样，一个是从边给出约束条件（匹配），一个是从结点给出约束条件（覆盖），但是都是对于一张二分图的描述，那么这两个之间存在什么关系呢？

我们拍脑袋想嘛，应该是匹配的边的数量一般会小于覆盖的节点数（因为这是简单图，一个边只能有2个节点，但是节点可以有多个边），而且，匹配的边一般是二分图的边的子集，而覆盖的结点多半会有重复的，也就是存在冗余。

因此，如果以匹配的最大边数为匹配数，以覆盖的最小节点数为覆盖数，则其两者相等。

数学就是，来一个定理，就要给出证明。这是个两个数相等的证明，一般证明使用“夹逼”方法。

1） $首先证明匹配数\alpha \le覆盖数\beta$
设M是二分图的最大匹配，S为二分图的最小覆盖。由于M中没有两边存在公共节点，并且M中的 $\alpha$条边每边至少有一个结点在S中，所以 $\alpha \le \beta$。后半句容易理解，因为每条边至少会有一个节点在S中，否则S就不是覆盖了。而前半句旨在说明 $\alpha$是不重不漏计数的，因此后半句才能够成立。

2） $接着证明匹配数\alpha \ge覆盖数\beta$
由第一节中相异代表系最大子集数推论（6.1.1）可知，一定存在整数k，选择 $i_1,i_2,...,i_k$使得 $|A_{i1}\cup A_{i2}\cup ...\cup A_{ik}|+(n-k)=\alpha$

然后，考虑证明 $T=(A_{i1}\cup A_{i2}\cup ...\cup A_{ik}) \cup (X-\{i_1,i_2,...,i_k\})$为覆盖即可。可从两个方面考虑，任取一条边[x,y].
一、当 $x \in \{i_1,i_2,...,i_k\}$时，存在一个点 $x=i_l$，使得 $y\in A_{il}$，从而 $y\in T$.
二、当 $x \in X-\{i_1,i_2,...,i_k\}$时，则 $x\in T$。

这样[x,y]都在T中，又因为
$|T|=|A_{i1}\cup A_{i2}\cup ...\cup A_{ik}|+|X-\{i_1,i_2,...,i_k\}|$
$=|A_{i1}\cup A_{i2}\cup ...\cup A_{ik}|+(n-k)=\alpha$
因此T是具有 $\alpha$个节点的覆盖，而 $\beta$是最小覆盖，因此 $\alpha \ge \beta$

综上所述 $\alpha=\beta$

3. 二分图的匹配算法

盖饭算法是来判断一个二分图的匹配M是否是最大匹配。如果不是，如何修改M得到更多的匹配，依此循环从而获得最大匹配。

3.1交错链

由于交错链有一个特性即在关于M的交错链中，不在M中的边数比在M中的边数多1，因此当我们反转其边时，就可以获得更多的边了。

首先给出基本链的定义：

基本链有一些性质：
若n为偶数，则基本链的边数为偶数，此时头结点 $u_0$和尾结点 $u_n$同属于X或同属于Y
若n为奇数，则基本链的边数为奇数，此时头结点 $u_0$和尾结点 $u_n$分别属于X和Y。

正是有这样的特殊性质，才有了交错链的存在：

例如：
经过这一次变换，就增加了一条边在M中，现在有4条边了。但是有5个节点，因此接下来，还可以再试一把。

有了交错链就可以找到最大匹配了。

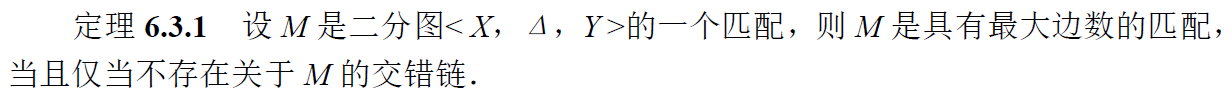
有了定理，本来是该高兴的事，但是有定理就要证明。

首先证明必要性，即若M是具有最大边数的匹配，则不存在关于M的交错链（==>）。

如图所示，假设存在r是M的一个交错链，则 $|N_0|=|M_0|+1$，令 $M'=(M-M_0)\cup N_0$，由于 $N_0$和 $(M-M_0)$都是而二分图的一个匹配，如果 $M-M_0$与 $N_0$没有公共节点，那么 $M'$就是比 $M$多1条边的匹配。

下面证明 $M-M_0$与 $N_0$没有公共节点，设 $[x,y] \in N_0$。

1）若 $[x,y]$是首边（或尾边），如图所示，x不在 $M$中，y在M中，因此y不在 $M-M_0$中，因此 $[x,y]$不在 $M-M_0$中。

2）若[x,y]是中边，则x,y都在 $M_0$,显然不在 $M-M_0$中。

综上所述， $M-M_0$与 $N_0$没有公共节点，因此 $M'$就是比 $M$多1条边的匹配，与原条件不符，反证结束。

然后证明充分性，如图所示，在交错链中，红色的比蓝色的多一条边。

3.2 寻找最大匹配算法

有了上面这条定理，我们就可以实现以下寻找最大匹配的算法了。

这里我们先给出例子，然后再给出第一步结束的证明。

通过第一步，就可以找到这条红蓝相间的交错链，此时是到第二步停止。我们使用红色代替蓝色，将红色置为粗体（在M中），蓝色变回正常（不在M中），从而得到新的匹配。

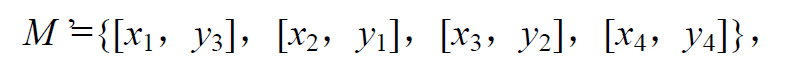
再在M中再执行一次算法，可以得到红蓝边数相等，此时已经无法继续增加匹配中边的数量了，因此此时算法结束， $M'$为最大匹配。

虽然我们从直观上可以发现并不能继续增加更多的边了，但是数学上，要讲究证明，即证明定理6.3.2。

该定理就是要证明，若S是覆盖，且 $|S|=|M|$，则M是最大匹配。

这里面说的比较拗口，因为是完全从具体说法上的解释。在证明第一个时，其反证法主要证明若 $e=[x,y]$不在S中，以两种情况考虑即 $e \in M$和 $e \notin M$；证明第二个则以x和y两个角度考虑。其核心是在算法的过程中体现出来的。

3.3 判断一个图是否为二分图

这里增加一个题目，就是如何判断一个图是二分图？

当然无脑想法就是暴力解决，按照循环去遍历不同的划分使得该图可以成为两部分，再判断两部分内部是否有无相连的边。

但是这样时间复杂度上至少是 $O（n^3）$。如果能先进行一次划分，再去判断多好？根据二分图的性质，在图中，任意选取一点，将其与其连接的点按照边数长度奇偶划分成两部分，再判断这两部分是否内部有相连即可，此时可以减少至 $O(n^2)$。当然，也可以使用广度优先算法[代码]进行黑白着色，从而判断一个图是否是二分图（时间复杂度也是 $O（n^2）$）。

当然也可以从，若一个图不存在奇数环，则该图是二分图入手，证明一个图不存在奇数环即可，这个等价定理还需要证明才能够实现。