1 说明
如果一个问题具有以下两个要素：
• 最优子结构(optimal substructure)
• 重叠子问题(overlap subproblem)
则可以用动态规划求最优解。
动态规划分为4 个步骤：
•（1）描述最优解的结构。即抽象出一个状态来表示最优解。
•（2）递归的定义最优解的值。找出状态转移方程，然后递归的定义
•（3）计算最优解的值。典型的做法是自底向上。
•（4）根据计算过程中得到的信息，构造出最优解。如果我们只需要最优解的值，不需要最优解本身，则可以忽略第4 步。当执行第4 步时，我们需要在第3 步的过程中维护一些额外的信息，以便我们能方便的构造出最优解。

在第1 步中，我们需要抽象出一个“状态”，在第2 步中，我们要找出“状态转移方程”，然后才能递归的定义最优解的值。第3 步和第4 步就是写代码实现了。
1.1 举例1 Leetcode 198.打家劫舍
1.1.1 题目描述
Leetcode 198.打家劫舍
你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。

示例 1:
输入: [1,2,3,1]
输出: 4
解释: 偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。

示例 2:
输入: [2,7,9,3,1]
输出: 12
解释: 偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
1.1.2 分析
考虑所有可能的抢劫方案过于困难。一个自然而然的想法是首先从最简单的情况开始。记：
f(k) = 从前 k 个房屋中能抢劫到的最大数额，A I = 第 i 个房屋的钱数。
首先看 n = 1 的情况，显然 f(1) = A1。
再看 n = 2，f(2) = max(A1, A2)。
对于 n = 3，有两个选项:
抢第三个房子，将数额与第一个房子相加。
不抢第三个房子，保持现有最大数额。
显然，你想选择数额更大的选项。于是，可以总结出公式：
f(k) = max(f(k – 2) + Ak， f(k – 1))。
也就是说：
动态规划方程：dp[n] = MAX( dp[n-1], dp[n-2] + num )
1.1.3 代码
int maxData(int a, int b) {
return a > b ? a : b;
}
int rob(int* nums, int numsSize){
//前面几个情况的处理
if(numsSize <= 0) {
return 0;
}
if(numsSize == 1) {
return *nums;
}
if(numsSize == 2) {
return maxData(nums[0], nums[1]);
}
int i = 0;
int dp[numsSize];
dp[0] = nums[0];
dp[1] = maxData(nums[0], nums[1]);

//根据状态转移方程计算
for(i = 2; i < numsSize; i++) {
    dp[i] = maxData(dp[i - 1], dp[i - 2] + nums[i]);
}

return dp[numsSize - 1];

}
1.2 举例2 leetcode 213.打家劫舍II
1.2.1 题目描述
你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都围成一圈，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。

示例 1:
输入: [2,3,2]
输出: 3
解释: 你不能先偷窃 1 号房屋（金额 = 2），然后偷窃 3 号房屋（金额 = 2）, 因为他们是相邻的。

示例 2:
输入: [1,2,3,1]
输出: 4
解释: 你可以先偷窃 1 号房屋（金额 = 1），然后偷窃 3 号房屋（金额 = 3）。
偷窃到的最高金额 = 1 + 3 = 4 。
1.2.2 分析
在198.打家劫舍的基础上，分成两种情况：
第一种情况，访问第一家，不访问最后一家，也就是1 ~ (n-1)的情况
第二种情况，不访问第一家，访问最后一家，也就是2 ~ n的情况
最后返回两种情况里面的大值。
1.2.3 代码
int maxData(int a, int b) {
return a > b ? a : b;
}
int rob(int* nums, int numsSize){
//前面几个情况的处理
if(numsSize <= 0) {
return 0;
}
if(numsSize == 1) {
return *nums;
}
if(numsSize == 2) {
return maxData(nums[0], nums[1]);
}
if(numsSize == 3) {
return maxData(maxData(nums[0], nums[1]), nums[2]);
}

//第一种情况，访问第一家，不访问最后一家，也就是1 ~ (n-1)的情况
int i = 0;
int dp[numsSize - 1];
dp[0] = nums[0];
dp[1] = maxData(nums[0], nums[1]);

for(i = 2; i < numsSize - 1; i++) {
    dp[i] = maxData(dp[i - 1], dp[i - 2] + nums[i]);
}

//第二种情况，不访问第一家，访问最后一家，也就是2 ~ n的情况
int dp2[numsSize - 1];
dp2[0] = nums[1];
dp2[1] = maxData(nums[1], nums[2]);

for(i = 3; i < numsSize; i++) {
    dp2[i - 1] = maxData(dp2[i - 1 - 1], dp2[i - 1 - 2] + nums[i]);
}

return maxData(dp[numsSize - 2], dp2[numsSize - 2]);

}
2 最长公共子序列
2.1 题目描述
Leetcode1143.最长公共子序列
给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列。
一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。
例如，“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。
若这两个字符串没有公共子序列，则返回 0。

示例 1:
输入：text1 = “abcde”, text2 = “ace”
输出：3
解释：最长公共子序列是 “ace”，它的长度为 3。

示例 2:
输入：text1 = “abc”, text2 = “abc”
输出：3
解释：最长公共子序列是 “abc”，它的长度为 3。

示例 3:
输入：text1 = “abc”, text2 = “def”
输出：0
解释：两个字符串没有公共子序列，返回 0。

提示:
1 <= text1.length <= 1000
1 <= text2.length <= 1000
输入的字符串只含有小写英文字符。
2.2 分析
状态转移方程为：

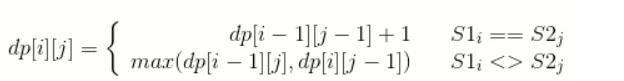
2.3 代码
int maxData(int a, int b) {
return a > b ? a : b;
}
int longestCommonSubsequence(char * text1, char * text2){
int text1Len = strlen(text1);
int text2Len = strlen(text2);
if(text1Len <= 0 || text2Len <= 0) {
return 0;
}
int i = 0, j = 0;
int dp[text1Len][text2Len];
//先初始化为0
for(i = 0; i < text1Len; i++) {
for(j = 0; j < text2Len; j++) {
dp[i][j] = 0;
}
}

//初始化边界值  
bool equalFlg = false;
for(i = 0; i < text1Len; i++) {
    if(text1[i] == text2[0]) {
        equalFlg = true;
    }
    if(equalFlg) {
        dp[i][0] = 1;
    }
}
equalFlg = false;
for(i = 0; i < text2Len; i++) {
    if(text2[i] == text1[0]) {
        equalFlg = true;
    }
    if(equalFlg) {
        dp[0][i] = 1;
    }
}

//根据状态转移函数写代码
for(i = 1; i < text1Len; i++) {
    for(j = 1; j < text2Len; j++) {
        if(text1[i] == text2[j]) {
            dp[i][j] = dp[i - 1][j - 1] + 1;
        }
        else {
            dp[i][j] = maxData(dp[i - 1][j], dp[i][j - 1]);
        }
    }
}

return dp[text1Len - 1][text2Len - 1];

}