以下是多尺度协同变异的粒子群优化算法的实验报告，主要是对传统的粒子群算法引入了混合高斯变异算子，来进行粒子的逃逸，从而使得目标函数可以更好更快的收敛到最优值。

1.问题描述

粒子群算法通过设计一种无质量的粒子来模拟鸟群中的鸟，粒子仅具有两个属性：速度和位置，速度代表移动的快慢，位置代表移动的方向。每个粒子在搜索空间中单独的搜寻最优解，并将其记为当前个体极值，并将个体极值与整个粒子群里的其他粒子共享，找到最优的那个个体极值作为整个粒子群的当前全局最优解，粒子群中的所有粒子根据自己找到的当前个体极值和整个粒子群共享的当前全局最优解来调整自己的速度和位置。

多尺度协同变异的自适应粒子群算法(multi-scale cooperative mutatingly selfadaptive escape PSO,简称 MAEPSO).该算法利用不同大小方差的自适应高斯变异机制实现解空间的探索,这种多个或大或小的变异机制能够促使整个种群以尽量分散的变异尺度来对解空间进行更加详尽的探索。最终使得算法得到较好的收敛效果。

2.算法设计

2.1 算法流程

传统的PSO算法仅仅是根据当前位置与全局最优位置进行位置与速度的更新，而多尺度协同变异的粒子群算法则是引入了多尺度高斯变异算法来进行位置的更新操作，在每次变异之后，在根据粒子群的位置来更新该多尺度高斯变异算子的方差。接着根据变异的次数等信息来更新高斯变异算法的阈值。从而促使整个种群可以有效的进行变异，最终使得算法得到较好的收敛效果。

算法流程图如下图所示。

                                                                                         图2.1 算法流程图

2.2 基础位置更新

一个由m个粒子组成的群体在n维搜索空间中以一定速度 飞行,每个粒子在搜索时根据目前为止自身搜索到的历史最好点  (也称为pbest)和整个群体中所有粒子发现的最好点  (也称为gbest)进行位置 xi= 的变化. 粒子迭代过程中速度与位置的更新公式为

(1) 

(2) 

其中c1,c2是学习因子，r1,r2是[0,1]之间的随机数，使得粒子以一定的概率根据自身位置与全局最优位置调整本身的位置信息。

2.3 多尺度高斯变异算子

设尺度个数为M,首先初始化多尺度高斯变异算子的方差:

(3) 

初始时,方差一般设定为优化变量的取值范围;随着迭代次数的增加,多尺度高斯变异算子的方差会随之进行调整,具体调整方式如下:首先,对种群中的粒子进行组合,生成M个子群,每个子群的粒子个数为P=N/M, K是当前迭代次数,计算每一个子群的适应度值:

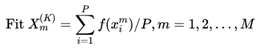
(4) 

不同变异尺度之间相互竞争,根据适应能力的不同设置不同的变异能力.因此,第m个变异算子的标准差为

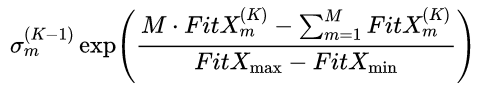
(5) 

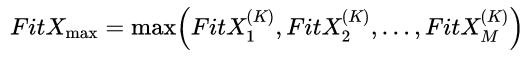
(6) 

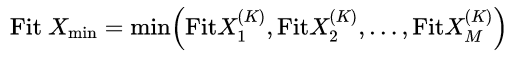
(7) 

对变异算子的标准差作如下规范

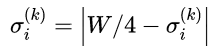
(8) 

我们根据多尺度高斯变异算法对粒子进行位置的更新

(9) 

其中 是实现设置好的阈值，超过了阈值则给该粒子一个逃逸的操作，这是算法的关键，这是使得算法不易陷入到局部最优位置，更加容易的去找到全局最优解。

阈值的大小将会对算法的执行效果产生一定影响:如果阈值过大,则会导致逃逸次数增加, 从而打乱PSO种群进化的原有结构,使算法无法进行局部深度搜索,开采能力下降;阈值过小,则会导致微粒速 度需较长时间达到逃逸条件,在有限的迭代次数内无法进行有效的全局搜索,勘探能力下降.

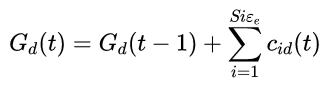
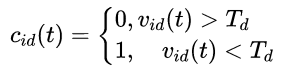
(10) 

其中,k1,k2为常数,Size为种群大小,频率 表示种群第d维速度曾经发生逃逸的总次数.k1标记调整阈值 和频率 的条件值,k2用来控制阈值速度下降的幅度.通过控制粒子飞行速度的方式,不仅能够保证算法的全局解空间勘探性能,同时在算法后期还能使粒子群进行精确的局部搜索,保证算法的收敛速度.

3.程序流程

1.初始化城市序列的坐标

1.随机初始化粒子群的位置，速度等信息，并且计算机当前粒子的全局最优位置以及当前粒子的最优位置。

2.利用公式(1)(2)进行粒子位置，速度的更新。

3.根据公式(9)判断当前粒子是否需要进行逃逸操作，如果需要根据多尺度高斯变异算子对粒子的位置，速度进行更新。

4.用公式(4)(5)(6)(7)(8)来对多尺度高斯变异算法进行方差的更新。

5.用公式(10)对逃逸操作的阈值进行更新。

6.判断是否达到迭代次数，如果没有转到第2步，达到的话转到第7步。

7.输出适应度最好的粒子。

4.源代码

#include <iostream>
#include <numeric>
#include <vector>
#include <time.h>
#include <math.h>
#include <stdlib.h>
#include <locale>
#include <string>
#include <algorithm>
#include <fstream>

#define PI 3.1415927
//#define INF numeric_limits<double>::max()

using namespace std;

int Size = 20;
int M = 5;
int dim = 30;
int W = 100;
float c1 = 1.4;
float c2 = 1.4;
float w_max = 0.5; //c1,c2，w_max需要根据不同的函数进行修改 
float w_min = 0.4;
float w = w_max;
int P = (int)(Size / M);
double INF = pow(10, 10.0);
string choice="Tablet"; //"Quadric"

vector<vector<double> >  X(Size, vector<double>(dim, 0));
vector<vector<double> > pb(Size, vector<double>(dim, 0));
vector<vector<double> > V(Size, vector<double>(dim, 0));
vector<double> T(dim, 0.5);
vector<double> G(dim, 0);
vector<double> gb(dim, 0);
vector<double> sigma(M, 2*W);


double function(vector<double> X){
	double sum = 0;
	if(choice=="Tablet")
	{
		sum = pow(10, 6.0)*pow(X[0],2.0);
		for(int i = 1; i < X.size(); ++i){
			sum += pow(X[i],2.0);
		}
	}
	else if(choice=="Quadric")
	{
		for(int i = 0; i < X.size(); ++i)
		{
			double temp_sum = 0;
			for(int j = 0; j <= i; ++j)
			{
				temp_sum += X[j];
			}
			sum += temp_sum*temp_sum;
		}
	}
	else if(choice=="Rosenbrock")
	{
		for(int i = 0; i < X.size()-1; ++i)
		{
			sum += 100*pow( (X[i+1]-X[i]*X[i]), 2.0) + (X[i]-1)*(X[i]-1);
		}
	}
	else if(choice=="Griewank")
	{
		double sum1 = 0, sum2 = 1;
		for(int i = 0; i < X.size(); ++i)
		{
			sum1 += X[i]*X[i];
			sum2 *= cos((X[i]/sqrt((i+1)*1.0))); //弧度？？？
		}
		sum = sum1/(4000.0) - sum2 + 1;
	}
	else if(choice=="Rastrigin")
	{
		int A = 10;
		for(int i = 0; i < X.size(); ++i)
		{
			sum += X[i]*X[i] - A*1.0*cos(2*PI*X[i]) + A;
		}
	}
	else if(choice=="SchafferF7")
	{
		for(int i = 0; i < X.size()-1; ++i)
		{
			sum += pow((X[i]*X[i]+X[i+1]*X[i+1]), 0.25) * (sin(50.0*pow(X[i]*X[i]+X[i+1]*X[i+1], 0.1)) + 1.0);
		}
	}


	return sum;
}



vector<double> func(vector<vector<double> >& X)
{
	vector<double> fit;
	for(int i = 0; i < X.size(); ++i)
	{
		fit.push_back(function(X[i]));
	}

	return fit;
}

//产生正太分布
double sampleNormal()
{
	double u = ((double)rand()/RAND_MAX)*2 - 1;
	double v = ((double)rand()/RAND_MAX)*2 - 1;
	double r = u*u + v*v;
	if(r==0 || r>1)
		return sampleNormal();
	double c = sqrt(-2*log(r)/r);
	return u*c;
}

bool cmp(vector<double> a, vector<double> b)
{
	return function(a) < function(b);
}

void init_sort(vector<vector<double> >& a)
{
	for(int i = 0; i < a.size(); ++i)
	{
		for(int j = i+1; j < a.size(); ++j)
		{
			if(function(a[i]) > function(a[j]))
			{
				vector<double> t = a[j];
				a[j] = a[i];
				a[i] = t;
			}
		}
	}
}

void init(){
	for(int i = 0; i < Size; ++i)
	{
		for(int j = 0; j < dim; ++j)
		{
			double rand1 = ((double)rand()*2/RAND_MAX-1)*W;
    		double rand2 = ((double)rand()*2/RAND_MAX-1);
    		X[i][j] = rand1;
    		pb[i][j] = rand1;
    		V[i][j] = rand2;
		}
	}

	//init_sort(X); //这里的排序似乎不起作用
	//init_sort(pb);
	//sort(X.begin(), X.end(), cmp);
	//sort(pb.begin(), pb.end(), cmp);

	vector<double> fit(func(X));
	double min = INF;
	int min_idx = -1;
	for(int i = 0; i < fit.size(); ++i)
	{
		if(min > fit[i]){
			min = fit[i];
			min_idx = i;
		}
	}
	gb.assign(X[min_idx].begin(), X[min_idx].end());


}


void update_vp(){
	for(int i = 0; i < Size; ++i)
	{
		for(int j = 0; j < dim; ++j)
		{
			double rand1 = rand()*1.0/RAND_MAX;
			double rand2 = rand()*1.0/RAND_MAX;
			V[i][j] = w*V[i][j] + c1*rand1*(pb[i][j]-X[i][j]) + c2*rand2*(gb[j]-X[i][j]);

			if(fabs(V[i][j]) < T[j])
			{
				G[j] += 1;
				double min_f = INF*1.0;
				int min_ind = 0;
				double temp_x = X[i][j];
				vector<double> randn_sigma;
				for(int k = 0; k < M; ++k)
				{
					randn_sigma.push_back(sampleNormal()*sigma[k]);
				}
				for(int m = 0; m < M; ++m)
				{
					X[i][j] = temp_x + randn_sigma[m];
					double temp_f = function(X[i]);
					if(temp_f < min_f)
					{
						min_f = temp_f;
						min_ind = m;
					}
				}

				double Vmax = W - fabs(X[i][j]);
				//double Vmax = W - fabs(temp_x);
				double rand3 = (rand()*2.0/RAND_MAX-1);
				X[i][j] = temp_x + rand3*Vmax;
				if(min_f < function(X[i]))
				{
					V[i][j] = randn_sigma[min_ind];
				}
				else{
					V[i][j] = rand3*Vmax;
				}

				X[i][j] = temp_x;
			}

			X[i][j] += V[i][j];
			if (function(pb[i])>function(X[i]))
			{
				pb[i].assign(X[i].begin(), X[i].end());
			}
			if(function(gb)>function(pb[i]))
			{
				gb.assign(pb[i].begin(), pb[i].end());
			}

		}
	}
}

double FitX(int m)
{
	vector<vector<double> > sub_group;
	for(int i = (m-1)*P; i < m*P; i += P)
	{
		sub_group.push_back(X[i]);
	}
	vector<double> sub_f = func(sub_group);
	double sum = 0;
	for(int i = 0; i < sub_f.size(); ++i)
	{
		sum += sub_f[i];
	}

	return sum/(P*1.0);

}

void update_sigma(){
	vector<double> FitXs;
	double max_FitX = -INF;
	double min_FitX = INF;
	double total_FitX = 0;
	for(int i = 0; i < M; ++i)
	{
		double fit = FitX(i+1);
		total_FitX += fit;
		FitXs.push_back(fit);
		if(fit>max_FitX)
		{
			max_FitX = fit;
		}
		if(fit<min_FitX)
		{
			min_FitX = fit;
		}
	}

	for(int i = 0; i < M; ++i)
	{
		sigma[i] *= exp( (M*FitXs[i]-total_FitX)/(max_FitX-min_FitX+pow(10,-10.0) ) );
		while(sigma[i]>(W/4.0))
		{
			sigma[i] -= W/4.0;
		}
	}
}

void update_t()
{
	int k1 = 5, k2 = 10;
	for(int i = 0; i < dim; ++i)
	{
		if(G[i]>k1)
		{
			T[i] /= k2*1.0;
			G[i] = 0;
		}
	}
}

void evolve(int step, int epoch){
	vector<double> result;
	//ofstream outf;
	string path = "D:/result/" + choice + ".txt";
	//outf.open(path);
	for(int i = 0; i < epoch; ++i)
	{
		init(); //每次都要进行初始化
		for(int j = 0; j < step; ++j)
		{
			update_vp(); //更新粒子的速度与位置
			update_sigma();	//更新多尺度高斯算法的方差
			update_t(); //更新逃逸的阈值

			w = w_max - (w_max-w_min)*j/step*1.0;//HPSO论文(3)，消除速度惯性部分的公式
			if(function(gb)==0)
			{
				cout << "finished" << endl;
				break;
			}
			double temp_res = function(gb);
			cout << i << "   " << j << "   " << temp_res << endl;
			//outf<< i << "   " << j << "   " << temp_res << endl;
		}

		double res = function(gb);
		result.push_back(res);
		cout << "===============================" << endl << i << "\t\t\t" << res << endl;
		//outf << "===============================" << endl << i << "\t\t\t" << res << endl; //输出每次迭代结果到txt中
		for(int i = 0; i < gb.size(); ++i)
		{
			cout << gb[i] << '\n';
			//outf << gb[i] << '\n';
		}

	}
	//outf << "===============================" << endl << c1 << "   " << c2 << "   " << w_min << "   " << w_max << endl; //输出本次epoch的参数
	//outf.close();
}

int main()
{
	//init();
	evolve(6000, 1);

	return 0;
}

5.代码运行及测试

本实验的测试函数选用下表中的六个函数。

                                                                                       表5-1 测试函数表

以下是本实验实现了多尺度高斯变异算子的粒子群算法对表5-1中六个函数的测试结果。

                           (a) Tbale                                                    (b)Quadric

                         (c)Rosenbrock                                            (d)Griewank

                        (e)Rastrigin                                                 (f)SchafferF7

                                                        图5.1 函数迭代图

从图5.1可以看出六个函数都可以较快的收敛到最小值0，而且基本上都在迭代1000次以内，特别是对于简单函数，几乎在300次以内就可以快速的得到收敛，充分证明了多尺度高斯变异算子的有效性。

下表5-2是六个函数在6000次迭代的时候，最终收敛到的最小值。

                                                                         表5-2 函数收敛值表

从表5-2可以更加清晰看出，所有函数基本都收敛到了接近于0的值，不过也有收敛情况不是特别好的时候，比如最后一个函数SchafferF7，虽然最后的收敛值也是接近于0，但是相比其他五个函数还是差的较远，极大的可能是由于函数的复杂性导致该算法陷入到了一个局部最优的值。结果难以收敛到一个更好的值。

6.结论

引入了多尺度高斯变异算子的粒子群算法确定可以对优化问题给出一定较好的解，而且往往可以实现较快的收敛。通过对六个函数进行实验，发现多尺度的高斯变异粒子群算法都可以较好的得到这六个函数的最优解。但是通过实验也发现，该算法对于参数的设置非常敏感，比如位置与速度的学习率等，轻微的改动可以较大的影响函数的收敛程度。

实验中也发现对于那些特别复杂的函数，该算法还是有一定局限性，函数值还是会陷入到一个接近于0的局部最优解中。这点还是有待完善的。

报告中的论文：https://wenku.baidu.com/view/b8da3f571a37f111f0855ba1.html

参考：

https://blog.csdn.net/daaikuaichuan/article/details/81382794

https://github.com/chenshen03/MAEPSO

https://wenku.baidu.com/view/5d469adb760bf78a6529647d27284b73f24236d2.html?re=view