一、常规方法
见poj 3219的方法，这一方法容易理解，只是超时。
对于输入的n、p，
for(i=0;i<=n;i++)
{
用前面的方法，分别计算n!、i!、（n-i）！中因子p的个数，再比较n!中因子p的个数与i!、（n-i）！中因子p的个数之和，来决定组合数C（n，i）是否能整除p；
如不能整除，计数器加1；
}
代码如下：
#include
using namespace std;
int jc(int N, int P)
{
int sum=0;
while(N)
{
sum=sum+N/P;
N=N/P;
}
return sum;
}
int n,m,p,ca=0;
int main()
{
while(scanf("%d%d",&p,&n))
{
if(p0 && n0)
break;
ca++;
int i,count=0;
int a=jc(n, p);
for(i=0;i<(n+1)/2;i++)
{
int b=jc(i, p);
int c=jc(n-i, p);
if(a<=b+c)
count++;
}
printf(“Case %d: %04d\n”,ca,2*count);
}
system(“pause”);
return 0;
}

二、Lucas定理
仍然超时，只能用Lucas定理，只看结论：
1、Lucas定理：
因为，对任何数有：n = n/pp + n%p（n/p取整）
所以：对任意数n和m，质因数p，则组合数c(n,m)与组合数C(n/p,m/p)C(n%p,m%p)同余。
也即是：令n=sp+q , m=tp+r .（q ，r ≤p）
那么：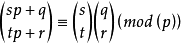
2、本题解法
而本题的大致解法是：
给n,p，n=akp^k+a(k-1)*p(k-1)+…+a2p^2+a1p+a0，也就是，n的p进制表示为（ak,…,a2,a1,a0）
那么，在组合数c(n,0),c(n,1)…c(n,n-1),c(n,n)中，不能被P整除的数一共有(a0+1)(a1+1)…(ak+1)，

#include
using namespace std;
int main()
{
int p,n,ca=0;
while(cin>>p>>n)
{
if(p0 && n0)
break;
int ans=1;
while(n)
{
ans=ans*(n%p+1);
n=n/p;
if(ans>=10000)
ans=ans%10000;

	}
	printf("Case %d: %04d\n",++ca,ans);
}
system("pause");
return 0; 

}