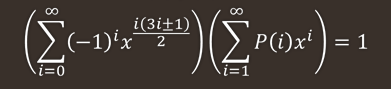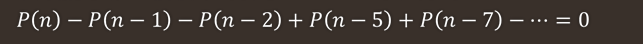前言

疯狂盗图

五边形数

$f_n=1+4+7+...+3*(n-1)+1=\frac{3n^2-n}{2}$
定义 $p_n=\frac{i(3i\pm1)}{2}$ 为广义五边形数

五边形数定理

$\phi(x)=\prod_{i=1}^{+\infty}(1-x^i)=\sum_{i=-\infty}^{+\infty}(-1)^i*x^{\frac{i(3i-1)}{2}}=\sum_{i=0}^{+\infty}(-1)^i*x^{\frac{i(3i\pm1)}{2}}$
此时 $f(n)=$偶数个数的拆分方案数-奇数个数的拆分方案数，并且要求拆分的数是不同的
利用 $Ferrers$ 图像进行探究


即大多数情况对于一个奇数拆分存在一个共轭偶数拆分
但是有一些例外情况：

还有

的拆分没有共轭的两组形式，那么系数就为 $(-1)^s$

可重整数拆分和五边形数

定义 $P(x)=\prod_{i=1}^{+\infty}(1+x^i+x^{2i}+...)$
显然有 $P(x)=\prod_{i=1}^{+\infty}\frac{1}{1-x^i}$
结合之前的

$\phi(x)=\prod_{i=1}^{+\infty}(1-x^i)=\sum_{i=-\infty}^{+\infty}(-1)^i*x^{\frac{i(3i-1)}{2}}=\sum_{i=0}^{+\infty}(-1)^i*x^{\frac{i(3i\pm1)}{2}}$
也就是
$\phi(x)P(x)=1$

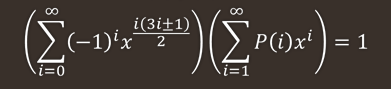
然后就能对比系数

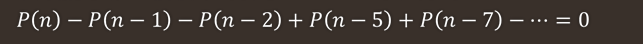
时间复杂度为 $O(n\sqrt n)$

两个题目

题目一HDU4658

记 $F(x)=\prod_{i=1}^{+\infty}(1+x^i+x^{2i}+x^{(k-1)i})=\prod_{i=1}^{+\infty}\frac{1-x^k}{1-x}=\frac{\phi(x^k)}{\phi(x)}$
那么 $\phi(x)F(x)=\phi(x^k)$
结合 $\phi(x)P(x)=1$
那么 $F(x)=\phi(x^k)*P(x)$

预处理 $P$ 后再弄一次即可，时间复杂度 $O(n\sqrt n)$

题目二[NOOnline #1 入门组]魔法

基础的
题目解析