SVM
-
SVM(Support Vector Machines)定义
一个能使两类之间的空间大小最大的一个超平面。这个超平面在二维平面上看到的就是一条直线,在三维空间中就是一个平面…。因此,我们把这个划分数据的决策边界统称为超平面。离这个超平面最近的点就叫做支持向量,点到超平面的距离叫间隔。支持向量机就是要使超平面和支持向量之间的间隔尽可能的大,这样超平面才可以将两类样本准确的分开,而保证间隔尽可能的大就是保证我们的分类器误差尽可能的小,尽可能的健壮。
-
点到超平面的距离公式
-
超平面的方程:
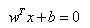
-
点到超平面的距离d的公式:
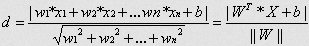
为超平面的范数
常数 类似于直线方程中的截距
为样本的中的一个点,其中 表示为第 个特征变量
-
-
核函数
对于非线性的情况,SVM 的处理方法是选择一个核函数,通过将数据映射到高维空间,来解决在原始空间中线性不可分的问题。
上图所述的这个数据集,是用两个半径不同的圆圈加上了少量的噪音生成得到的,所以,一个理想的分界应该是一个“圆圈”而不是一条线(超平面)。
只需要把它映射到 一个三维空间中,下图即是映射之后的结果,将坐标轴经过适当的旋转,就可以很明显地看出,数据是可以通过一个平面来分开的:

Clustering
-
距离度量
最常用的距离度量就是闵科夫斯基距离,其特例包括欧氏距离和曼哈顿距离:
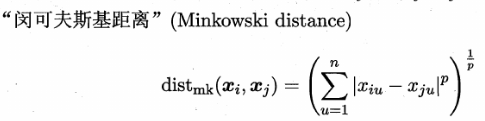


-
k-means算法

-
高斯混合聚类

-
密度聚类
此类算法假定聚类结构能通过样本分布的紧密程度确定。通常情况下,密度聚类算法从样本密度角度考察样本的可连接性,并基于可连接样本不断拓展聚类簇以得到最终聚类结果。
DBSCAN算法
-
层次聚类
层次聚类试图在不同层次上对数据集进行划分,从而形成树状的聚类结构。
LR
LR(Logistic Regression)逻辑回归
-
Logistic分布
-
Logistic分布函数如下:
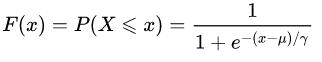
是位置参数, 是形状参数。 -
Logistic分布的密度函数如下:
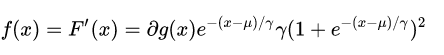
-
示意图

上图是不同参数对logistic分布的影响,从图中可以看到可以看到 影响的是中心对称点的位置, 越小中心点附近增长的速度越快。
在深度学习中用到的非线性变换sigmoid函数是逻辑斯蒂分布的 的特殊形式。
-
-
逻辑斯蒂回归模型
逻辑回归是为了解决分类问题,目标是找到一个有足够好区分度的决策边界,从而能够将两类很好的分开。
已知一个事件发生的几率odds是指该事件发生与不发生的概率比值。
二分类 情况下即
取odds的对数就
- 逻辑回归的定义:
输出 的对数几率是由输入x的线性函数表示的模型,即逻辑斯蒂回归模型
- 逻辑回归的定义:
-
逻辑回归的似然函数、对数似然函数
参考详解 -
优化方法
参考详解 -
正则化
在目标函数中加上一个正则化项 即
正则化项一般会采用L1范数或者L2范数,分别为 。
-
L1范数
L1范数:
当采用梯度下降方式来优化目标函数时,对目标函数进行求导,正则化项导致的梯度变化当 是取1,当 时取 。 因此当 的时候, 会减去一个正数,导致 减小,而当 的时候, 会减去一个负数,导致 又变大,因此这个正则项会导致参数w_j$ 取值趋近于0,这就是为什么L1正则能够使权重稀疏。 -
L2范数
L2范数:
对它求导,得到梯度变化为 。同样的更新之后使得 的值不会变得特别大。在机器学习中也将L2正则称为weight decay,在回归问题中,关于L2正则的回归还被称为Ridge Regression岭回归。weight decay还有一个好处,它使得目标函数变为凸函数,梯度下降法和L-BFGS都能收敛到全局最优解。
L1正则化会导致参数值变为0,但是L2却只会使得参数值减小,这是因为L1的导数是固定的,参数值每次的改变量是固定的,而L2会由于自己变小改变量也变小。而公式中的 也有着很重要的作用,它在权衡拟合能力和泛化能力对整个模型的影响, 越大,对参数值惩罚越大,泛化能力越好。
-
GBDT
GBDT (Gradient Boosting Decision Tree) 梯度提升决策树
-
集成学习
集成学习方法中最主要的两种方法为Bagging和Boosting -
Bagging方法
通过对训练样本重新采样的方法得到不同的训练样本集,在这些新的训练样本集上分别训练学习器,最终合并每一个学习器的结果,作为最终的学习结果。
学习器之间彼此是相互独立的,这样的特点使得Bagging方法更容易并行。
最重要的算法为随机森林Random Forest算法。 -
Boosting方法
Boosting是一种递进的组合方式,每一个新的分类器都在前一个分类器的预测结果上改进。 -
GBDT
- GBDT表示
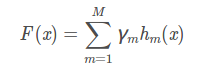
GBTD是一个加性模型,通过不断迭代拟合样本真实值与当前分类器的残差 来逼近真实值的,按照这个思路,第m个基分类器的预测结果为
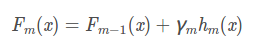
而 的优化目标就是最小化当前预测结果 和 之间的差距。
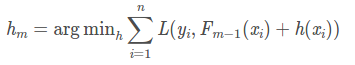
- GBDT表示