玄学之深度学习学习之路——数学基础2--概率论、数理统计与随机过程

概率分布

离散变量对应概率质量函数（就是离散变量的概率，加起来为1，教材叫分布律）

连续变量对应概率密度函数（积分为1）

边缘概率

已知一组变量的联合概率分布，其中变量的一个子集的概率分布称为边缘概率分布。

比如已知 $P(\textup{x},\textup{y})$ ，可以依据下面求和法则来计算 $P(\textup{x})$ ：

$\forall x \in \textup{x},P(\textup{x}=x)=\sum_{y}P(\textup{x}=x,\textup{y}=y)$

对于连续型变量，需要用积分替代求和：

$p(x)=\int p(x,y)dy$

条件概率

在 $\textup{x}=x$ 的条件下， $\textup{y}=y$ 发生的条件概率为：

$P(\textup{y}=y|\textup{x}=x)=\frac{P(\textup{y}=y,\textup{x}=x)}{P(\textup{x}=x)}$

条件概率只有在 $P(\textup{x}=x)>0$ 时有定义。

概率的链式法则或乘法法则：任何多维随机变量的联合概率分布，都可以分解成只有一个变量的条件概率相乘的形式：

扫描二维码关注公众号，回复： 12646315 查看本文章

$P(\textup{x}_{1},...,\textup{x}_{n})=P(\textup{x}_{1})\prod_{i=2}^{n}P(\textup{x}_{i}|\textup{x}_{1},...,\textup{x}_{i-1})$

独立性

如果两个随机变量 $\textup{x}$ 和 $\textup{y}$ 的概率分布可以表示成两个因子的乘积形式，且一个因子只包含x，另一个因子只包含y，则称这两个随机变量是相互独立的（可以扩展到n个随机变量）：

$\forall x \in \textup{x},y \in \textup{y},p(\textup{x}=x,\textup{y}=y)=p(\textup{x}=x)p(\textup{y}=y)$

如果关于 $\textup{x}$ 和 $\textup{y}$ 的条件概率分布对 $z$ 的每一个取值都能写成乘积的形式，那么这两个随机变量 $\textup{x}$ 和 $\textup{y}$ 在给定随机变量 $z$ 时是条件独立的：

$\small \forall x\in \textup{x},y \in \textup{y},z \in \textup{z},p(\textup{x}=x,\textup{y}=y|\textup{z}=z)=p(\textup{x}=x|\textup{z}=z)p(\textup{y}=y|\textup{z}=z)$

随机变量的独立性和事件的独立性是相通的。

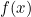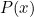函数 $\small f(x)$ 关于分布 $\small P(x)$ 数字特征

期望：

离散型： $\small \mathbb{E}_{\textup{x}\sim P[f(x)]}=\sum _{x}P(x)f(x)$

连续型： $\small \mathbb{E}_{\textup{x}\sim p[f(x)]}=\int p(x)f(x)dx$

方差：

$\small \textup{Var}(f(x))=\mathbb{E}[(f(x)-\mathbb{E}[f(x)])^{2}]$

标准差：方差的平方根

协方差：在某种意义上给出了两个变量线性相关性的强度以及这些变量的尺度：

$\small \textup{Cov}(f(x),g(y))=\mathbb{E}[(f(x)-\mathbb{E}[f(x)])(g(y)-\mathbb{E}[g(y)])]$

如果协方差的绝对值很大，意味着变量值变化很大，并且它们同时距离各自的均值很远。如果协方差是正的，那么两个变量都倾向于同时取得相对较大的值。如果协方差是负的，那么其中一个变量倾向于取得相对较大的值的同时，另一个变量倾向于取得相对较小的值。

相关系数：将每个变量的贡献归一化，为了只衡量变量的相关性：

$\small \rho _{f(x)g(y)}=\frac{\textup{Cov}(f(x),g(y))}{\sqrt{\textup{Var}(f(x)) \textup{Var}(g(y))}}$

协方差矩阵：随机向量 $\small \boldsymbol{x}\in \mathbb{R}^{n}$ 的协方差矩阵为：

$\small \textbf{Cov}(\textbf{x})_{i,j}=\textup{Cov}(\textup{x}_{i},\textup{x}_{j})$

常用的概率分布

0-1分布（伯努利分布）

对于一次试验，该试验的结果只有两种（要么是事件A发生，要么不是），结果定义为0和1，另结果为1的概率是p，那么0-1分布可以表达为

$P(X=k)=p^{k}(1-p)^{(1-k)}\; \;\;\;\;\;\;\;\;\;\; (k=0,1)$

记为 $X\sim b(1,p)$

二项分布

设某事件A在一次试验中发生的概率为p，重复n次试验，则事件A发生的次数i的概率的分布称为二项分布，其表达式为

$P(X=i)=\begin{pmatrix} n\\ i \end{pmatrix}p^i(1-p)^{(n-i)}\; \; \; \; \; \; \; (i=0,1,...,n)$

记为 $X\sim b(n,p)$ 。0-1分布是二项分布中n取1的特殊形式。

多项分布

多项分布是多维随机变量的分布，对于一次试验，其结果有k种，各种结果出现的概率分别为 $p_1$ , $p_2$ ,..., $p_n$ ，则重复n次试验，各种结果出现的次数分别为 $x_1$ , $x_2$ ,..., $x_n$ 的概率的分布称为多项分布，其表达式为

$P(X_1=x_1,X_2=x_2,...,X_k=x_k)=\frac{n!}{x_1!x_2!...x_k!}p_1^{x_1}p_2^{x_2}...p_k^{x_k}$ $(\sum_{i=1}^{n}x_i=n,x_i\geq 0)$

Multinoulli分布

Multinouli分布和多项分布的关系就像0-1分布和二项分布的关系，相当于是多项分布中n取1的形式。从而可知 $x_1$ , $x_2$ ,..., $x_n$ 的约束为

$\sum_{i=1}^{n}x_i=1,x_i\geq 0$

在这种情况下，各结果出现的概率为 $p_i$ 就表示了Multinouli分布。

泊松分布

泊松分布是在二项分布中满足 $p\to 0,n \to \infty$ 时的极限形式，它多出现在当 $X$ 表示在一定的时间或空间内出现事件个数这样的场合。具体地，假设观察的时间或空间的范围为 $[0,1)$ ，将该区间分成n个等长小段：

$l_1=[0,\frac{1}{n}),l_2=[\frac{1}{n},\frac{2}{n}),...,l_i=[\frac{i-1}{n},\frac{i}{n}),...,l_n=[\frac{n-1}{n},1)$

并且假定在各个小段之内：①事件 $X$ 发生一次的概率，近似地与段长 $\frac{1}{n}$ 成正比，即可取 $\frac{\lambda}{n}$ 。又假定n很大而段很小，在段内事件发生两次或以上是不可能的，则事件 $X$ 不发生的概率为 $1-\frac{\lambda}{n}$ 。②各段之内事件是否发生是独立的。根据这个假定可以知道 $X\sim b(n,\frac{\lambda}{n})$ ，于是事件X在范围内发生的 $x$ 次的概率就可以表达为

$P(X=x)=\binom{n}{x}(\frac{\lambda}{n})^x(1-\frac{\lambda}{n})^{(n-x)}$

当 $n \to \infty$ 时，就可以由上式得到泊松分布的表达

$P(X=x)=\frac{e^{-\lambda}\lambda^x}{x!}$

称 $X$ 服从泊松分布，记作 $X \sim p(\lambda)$ 。

当n很大且p很小时，我们可以用泊松分布来近似二项分布，此时取 $\lambda=np$ ，通过近似求取概率可以很大的降低计算量。

均匀分布

在离散型随机变量中，均匀分布可以视为随机变量 $X$ 可能的取值为n个不同的取值， $X$ 取到每个取值的概率都是 $\frac{1}{n}$ 。

我们更多的是讨论连续型随机变量中的均匀分布，其概率密度函数为

$r(x;a,b)=\left\{\begin{matrix} \frac{1}{b-a},\, \, \, \, a\leqslant x\leqslant b\\ 0,x< a\, or\, x>b \end{matrix}\right.$

正态分布

一维标准正态分布

$N(x;0,1)=\frac{1}{\sqrt{2\pi }}e^{-\frac{x^2}{2}}$

一维正态分布

$N(x;\mu,\sigma^2)=\frac{1}{\sqrt{2\pi }\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$

多维正态分布

$N(x;\boldsymbol{\mu },\mathbf{\Sigma })=\frac{1}{(2\pi )^n det(\boldsymbol{\Sigma})}e^{-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^T\boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})}$

其中 $\mathbf{\Sigma }$ 是正定对称矩阵，给出了分布的协方差矩阵。常把协方差矩阵固定成一个对角矩阵。

如果想要了解正态分布的发现和发展历程，可以阅读下面资料：

科学松鼠会 » 正态分布的前世今生（上） http://songshuhui.net/archives/76501

科学松鼠会 » 正态分布的前世今生（下） http://songshuhui.net/archives/77386

关于多元高斯分布的推导（介绍为什么是用协方差矩阵）：https://www.cnblogs.com/bingjianing/p/9117330.html

指数分布

From:如何推导指数分布的概率密度曲线？

指数分布可以定义为：在事件（关于时间t）没有发生的情况下，事件在下一个 $\Delta T$ 内发生的概率为

$\lim_{\Delta T \to 0}\lambda\Delta T$

（类似于泊松分布中分小段的假定，事件发生的概率与小区间长成正比，并且发生两次或以上次数的概率为0），那么事件在接下来的前n个 $\Delta T$ 内没有发生，而在第n+1个 $\Delta T$ 发生的概率为

$(1-\lambda\Delta T)^n\lambda\Delta T$

所以，事件在t时刻后的一个 $\Delta T$ 内发生的概率就等于

$(1-\lambda\Delta T)^{\frac{t}{\Delta T}}\lambda\Delta T$

于是可以写出事件关于时间t发生的概率分布函数为

$\lim_{\Delta T \to 0}F(t)=(1-\lambda\Delta T)^{\frac{t}{\Delta T}}\lambda\Delta T$

求导即得指数分布的概率密度函数为

$f(t;\lambda)=\lambda e^{-\lambda t}$

指数分布的一个重要性质是无记忆性（指数分布也可以定义为具有无记忆性的取值范围为0到正无穷的连续分布）。

拉普拉斯分布

如果随机变量的概率密度函数分布为

$f(x;\mu ,b)=\frac{1}{2b}e^ {-\frac {|x-\mu |}{b}}$

那么它就是拉普拉斯分布。其中， $\mu$ 是位置参数， $b > 0$ 是尺度参数。如果 $\mu = 0,b=1$ , 那么，正半部分恰好是 $\frac{1}{2}$ 倍 $\lambda=1$ 的指数分布。正态分布是用相对于 μ 平均值的差的平方来表示，而拉普拉斯概率密度用相对于平均值的差的绝对值来表示。因此，拉普拉斯分布的尾部比正态分布更加平坦。