A、代数部分
- 1、繁分式化简分式:
\(\cfrac{\frac{1}{a}+\frac{2}{b}+\frac{1}{c}}{\frac{3}{ac}-\frac{1}{b}+\frac{4}{bc}}=\cfrac{(\frac{1}{a}+\frac{2}{b}+\frac{1}{c})\times abc}{(\frac{3}{ac}-\frac{1}{b}+\frac{4}{bc})\times abc}=\cfrac{bc+2ac+ab}{3b-ac+4a}\);同乘
- 2、分式中负指数幂化为正指数幂:
\(\cfrac{a^x+a^{-x}}{a^x-a^{-x}}=\cfrac{(a^x+a^{-x})\times a^x}{(a^x-a^{-x})\times a^x}=\cfrac{a^{2x}+1}{a^{2x}-1}\);同乘
- 3、齐次式变形:
\(z=\cfrac{a+\sqrt{2}b}{\sqrt{2}a+b}\);分子分母同除以\(b\)变形得到,\(z=\cfrac{\frac{a}{b}+\sqrt{2}}{\sqrt{2}\frac{a}{b}+1}\xlongequal{t=\frac{a}{b}}\cfrac{t+\sqrt{2}}{\sqrt{2}t+1}\)
\(z=\cfrac{2a^2+4ab-3b^2}{a^2+ab+b^2}\);分子分母同除以\(b^2\)变形得到,\(z=\cfrac{2(\frac{a}{b})^2+4\frac{a}{b}-3}{(\frac{a}{b})^2+\frac{a}{b}+1}\xlongequal{t=\frac{a}{b}}\cfrac{2t^2+4t-3}{t^2+t+1}\)
\(a^2-5ab+4b^2>0\),不等式两端同除以\(b^2\)变形得到,\((\cfrac{a}{b})^2-5\cfrac{a}{b}+4>0\),这样我们能得到\(\cfrac{a}{b}<1\)或\(\cfrac{a}{b}>4\);
- 4、除法分配律(分数裂项)
\(①\cfrac{b+c}{a}=\cfrac{b}{a}+\cfrac{c}{a}\);
\(②\cfrac{a-b}{ab}=\cfrac{1}{b}-\cfrac{1}{a}\);(分式变形时常用)
但是她更多的时候表示为整式形式,如\(a_n-a_{n+1}=ka_{n+1}a_n\),
两边同除以\(a_{n+1}a_n\),可以变形为\(\cfrac{1}{a_{n+1}}-\cfrac{1}{a_n}=k\);
- 5、分子常数化(化为部分分式,也可以理解为使用了变量集中策略)
\(①y=\cfrac{2x-1}{x-1}=\cfrac{(2x-2)+1}{x-1}=2+\cfrac{1}{x-1}\);
\(②y=\cfrac{2x}{x+4}=\cfrac{2}{1+\frac{4}{x}}\);
\(③y=\cfrac{a^x-1}{a^x+1}=\cfrac{(a^x+1)-2}{a^x+1}=1-\cfrac{2}{a^x+1}\);
\(④y=\cfrac{2x^2-4x+3}{x-1}=\cfrac{2(x-1)^2+1}{x-1}=2(x-1)+\cfrac{1}{x-1}\);
B、几何部分
1、角平分线定理
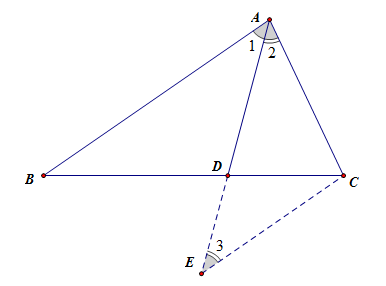
已知:如图所示,\(AD\)是\(\Delta ABC\)的内角\(A\)的角平分线,交\(BC\)于点\(D\)。
求证:\(\cfrac{AB}{AC}=\cfrac{BD}{DC}\)
证明:过点\(C\)作直线\(CE//AB\),并且交\(AD\)的延长线于点\(E\),
则可知\(\Delta ADB\sim \Delta EDC\),且有\(\cfrac{AB}{EC}=\cfrac{BD}{CD}①\);
又由\(AB//CE\)可知,\(\angle 1=\angle 3\),
又已知\(\angle 1=\angle 2\),故\(\angle 2=\angle 3\),
即\(CE=AC\),代入①式可得\(\cfrac{AB}{AC}=\cfrac{BD}{DC}\)。
以下内容待有时间补充。