线性筛 （欧拉筛）

1 线性筛的功能
可以用O(n)的时间去筛出 1 ~ n 的所有质数
2 代码

int prime(int x){
    
             //欧拉筛
    for(int i=2;i<=x;i++){
    
    
        if(!st[i]) p[cut++]=i;
        for(int j=0;p[j]<=x/i;j++){
    
    
            st[p[j]*i]=true;
            if(i%p[j]==0) break;
        }
    }
    return cut;
}

3 证明

• 1 素数定义
  如果数 S 若存在一个数T（除1外）可以被T整除，则称S为合数，否则为素数
  素数就是除1以外没有其他整数可以整除他的数。
• 2 思路
  因为一个合数一定有一个最小质因子，只需要用他的最小质因子筛掉，即可。
• 3 实现
  用for循环遍历，如果没有被标记，这说明此数为素数，则加入prime数组
  每次遍历就进行一次筛除，这里一定要只筛一次即可
  所以，我们特判
  若 i%p==0 说明 p 为 i 的最小质因子，这时我们就要退出循环（这样使筛法为线性）
  若 i%p!=0 则说明不是最小质因子，直到找到最小质因子，或本身为素数

题目 回文质数
代码如下

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cmath>
using namespace std;
const int N=1e8+10,M=N/log(N)+10;//一般有 N/lnN 个素数（常识）
int a,b;
int prime[M],cut;
bool st[N];
void get_prime(){
    
            //线性筛
    for(int i=2;i<=b;i++){
    
    
        if(!st[i]) prime[cut++]=i;
        for(int j=0;prime[j]<=b/i;j++){
    
    
            st[prime[j]*i]=true;
            if(i%prime[j]==0) break;
        }
    }
}
int main(){
    
    
    cin>>a>>b;
    if (b > 10000000) b=10000000;  //偶数位的回文数不是素数，直接去掉
    get_prime();
    int t=lower_bound(prime,prime+cut,a)-prime;
    for(int i=t;i<cut;i++){
    
    
        int k=prime[i];
        int ans=0;
        for(;k;k/=10) ans=(ans*10+k%10);  //制造回文数
        if(ans==prime[i]) printf("%d\n",ans);
    }
    return 0;
}

再来一道质数经典问题
质数距离
代码

#include<iostream>
#include<cstring>
#include<cmath>
using namespace std;
const int N=1e6+10;
int prime[500000],cut;
long long p[N],len;
bool st[N];
int l,r;
void get_prime(int n){
    
    
    memset(st,0,sizeof st);cut=0;
    for(int i=2;i<=n;i++){
    
    
        if(!st[i]) prime[cut++]=i;
        for(int j=0;prime[j]<=n/i;j++){
    
    
            st[prime[j]*i]=true;
            if(i%prime[j]==0) break;
        }
    }
}
int main(){
    
    
    while(scanf("%d%d",&l,&r)!=EOF){
    
    
        get_prime(sqrt(r)); len=0;
        memset(st,0,sizeof st);
        for(int i=0;i<cut;i++)
            for(int j=ceil((double)l/prime[i]);j<=r/prime[i];j++)
                if(j!=1) st[j*prime[i]-l]=true;
        for(int i=0;i<=r-l;i++){
    
    
            if(!st[i]&&i+l>1) p[len++]=i+l;
        }
        if(len<2) puts("There are no adjacent primes.");
        else{
    
    
            int maxn=1,minn=1;
            for(int i=2;i<len;i++){
    
    
                if(p[maxn]-p[maxn-1]<p[i]-p[i-1]) maxn=i;
                if(p[minn]-p[minn-1]>p[i]-p[i-1]) minn=i;
            }
            printf("%d,%d are closest, %d,%d are most distant.\n",p[minn-1],p[minn],p[maxn-1],p[maxn]);
        }
    }
    return 0;
}

欧拉函数

欧拉函数定义
对正整数n，欧拉函数是小于或等于n的正整数中与n互质的数的数目
（互质： gcd（a,b）==1的两个数）
欧拉函数公式

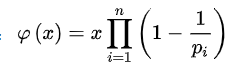
证明（容斥原理）

偷懒，哈哈
这里给一道欧拉函数题，可以思考一下（还是书上滴题目）
可见的点 欧拉函数
代码

#include<iostream>
#include<cstring>
using namespace std;
const int N=1010;
int prime[N],cut;
int phi[N];
bool st[N];
int c,n;
int phi_prime(){
    
    
    memset(st,0,sizeof st);cut=0;
    phi[1]=1;
    for(int i=2;i<=n;i++){
    
    
        if(!st[i]){
    
    
            prime[cut++]=i;
            phi[i]=i-1;
        }
        for(int j=0;prime[j]<=n/i;j++){
    
    
            st[prime[j]*i]=true;
            if(i%prime[j]==0){
    
    
                phi[prime[j]*i]=phi[i]*prime[j];
                break;
            }
            phi[prime[j]*i]=phi[i]*(prime[j]-1);
        }
    }
    int res=0;
    for(int i=1;i<=n;i++) res+=phi[i];
    return 2*res+1;
}
int main(){
    
    
    cin>>c;
    for(int i=1;i<=c;i++){
    
    
        cin>>n;
        printf("%d %d %d\n",i,n,phi_prime());
    }
    return 0;
}

欧拉定理和费马小定理

• 欧拉定理
  若n,a为正整数，且n,a互质
  
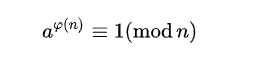
• 费马小定理
  基于欧拉定理
  若p为质数 p 的欧拉函数为 p-1，所以
  
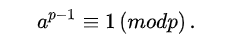
  证明了欧拉定理，就是证明了费马定理。
  费马定理相当与欧拉定理的特殊情况

证明欧拉定理（简单证明。如果看不懂，具体可以百度）

本人表达能力有限。害

经典题目
快速幂求逆元

证明

代码（求b的m-2次方）

#include<iostream>

using namespace std;
typedef long long ll;
int n;
int qmi(int a,int b,int p){
    
      //快速幂
    int res=1;
    for(;b;b>>=1){
    
    
        if(b&1) res=(ll)res*a%p;
        a=(ll)a*a%p;
    }
    return res;
}
int main(){
    
    
    cin>>n;
    while(n--){
    
    
        int a,p;
        scanf("%d%d",&a,&p);
        if(a%p) printf("%d\n",qmi(a,p-2,p));
        else puts("impossible");
    }
    return 0;
}