本博客整理自研读的论文，文末会附上出处。

一.背景

  在教育领域，随着云计算和移动互联网的发展，不同的学习平台产生了海量的教育大数据，包括个人数据、学习行为记录、交互数据等。 当前教育数据彼此分割、互操作不强，导致从中抽取、挖掘出有价值的个性化教育资源十分困难。 而教育资源的持续扩充和再生的速度远超出个体的信息处理能力，引发了信息过载，形成“资源越来越多、获取越来越难”的信息悖论。因此， 如何从大量的数据中筛选出有价值的信息，为学习者提供精准的、个性化的服务就成了一个现实问题。 在论文中我们想要解决关于如何为学习者找资源、为资源匹配学习者、为学习者寻找学习伙伴、为资源匹配资源（得到资源类簇）。
  接下来，我们主要解决两个问题：精准推荐和自适应聚类，这两个问题又可以各自细分为若干个小问题。

二.基于高阶奇异值分解的多模态推荐

基于高阶奇异值分解的（教育大数据）多模态推荐的步骤大致如下：

• 根据学习理论构建学习者、学习资源和学习轨迹三个子张量，然后分别从其中抽象出重要特征（或属性）作为子张量的阶，将三个子张量融合为一个大张量，如果有必要，我们还要对大张量进行简化操作；
• 将处理过的大张量进行高阶奇异值分解，并根据实际需求进行截断得到近似张量，由于大数据环境下的数据一般以增量方式产生，所以一般还需要对处理了的大张量进行追加后再进行近似处理；
• 当得到了一个近似张量，我们需要借助 Top-k来得到资源推荐张量（为学习者推荐资源）或学习推荐张量（为资源推荐学习者）从而实现精准推荐。

接下来就详细介绍这三个步骤。

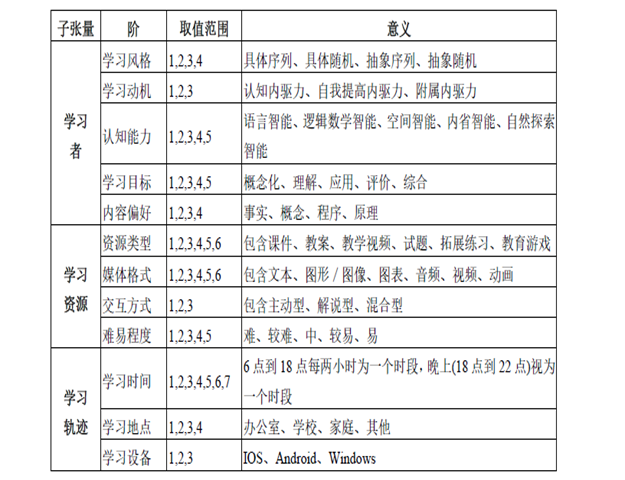
1.基于张量的教育大数据表示与融合（+简化）

  首先根据学习理论创建学习者、学习资源、学习轨迹三个子张量，这三个子张量能够表示不同来源且异构的教育大数据。构建这三个子张量需要分别抽取局部数据的特征，抽象出某些属性，比如对于学习者这个子张量抽取学号、偏好等属性作为张量的阶，然后根据实际需求去决定每个阶的维数，最后选择一种关联因素表示所有阶的关系并决定其数据类型，比如分别构建下列学习者、学习资源、学习轨迹子张量：

  学习轨迹张量将学习者张量和资源张量之间建立关联关系（学习轨迹张量与学习者张量在学号上有关联，学习轨迹张量与资源张量在资源号上有关联）。

  然后给定了某些子张量的属性和取值范围并且规定学习者、学习资源张量的数据类型为布尔类型，学习轨迹张量的数据类型为实数类型。

比如：
  在学习者张量中，L_xijkl…w=1 (布尔类型)代表第x个学生的学习风格为i，学习动机为j，认知能力为k，学习目标l，……，内容偏好为w
  在学习资源张量中，R_xijkl…w=1 (布尔类型) 代表第x 个资源的资源类型为i，媒体格式为j，交互方式为k，……，难易程度为w。
  在学习轨迹张量中，LR_xijk…w=3 (实数类型)代表学习者x 在时间i地点j，通过设备k，……，学习了资源w 的次数为3，0 则代表该学习者在当前情境下没有学习该资源。

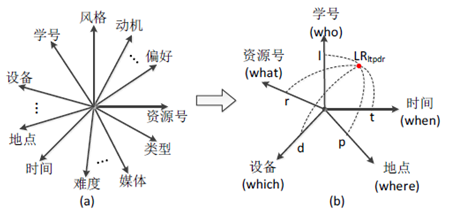
  为实现精准的个性化教育资源推荐，要求不破坏数据之间的固有关系对整体数据进行关联分析。为将学习者张量、资源张量和学习轨迹张量进行多视角关联分析，需要将三个张量模型进行关联融合，这需要用到张量连接这一操作。

  以上图为例：针对上面的学习者张量 L ，学习资源张量 R 和学习轨迹张量 LR ，可以先将学习者张量和学习轨迹张量沿着学号这一阶连接形成一个临时张量，然后再将这个临时张量和学习资源张量沿着资源号这一阶连接形成一个融合张量，形成的融合张量（见下图）。

张量简化 给定一个 $N$ 阶张量 $\underline{X}\in R^{I_1\times I_2\times \dots \times I_N},$ 则沿着 $pth,(p+1)th,\cdots ,qth$
阶从张量 $\underline{X}$ 进行抽取的部分张量为 $\underline{Y}\in R^{I_p\times I_{p+1}\times \dots X_q},$ 其元素为:
$$y_{i_p,\cdots ,i_q}=\sum _{i_1,\cdots ,i_{p-1},i_{q+1},\cdots ,i_N}^{I_1,\cdots ,I_{p-1},I_{q+1},\cdots ,I_N}{x}_{i_1,\cdots ,i_{p-1},i_p,\cdots ,i_q,i_{q+1},\cdots ,i_N}$$

  简单来说，张量简化就是对所有不需要的阶求和从而只保留需要的阶。
  根据拉斯韦尔的5w传播理论 （即5个w，Who（谁）Says What（说了什么） In Which Channel（通过什么渠道）To Whom （向谁说）With What Effect（有什么效果）），借此我们可以作出以下简化：

2.基于高阶奇异值分解的多维关联分析

  当个性化教育资源推荐系统从二维模型<用户，资源>发展到三维模型<用户，标签，资源>，多数推荐算法通常是把这个三维模型拆分成两个二维模型<用户，标签>和<资源，标签>来进行分析和推荐。这种拆分的方法失去了影响因素彼此之间的特征结构和关联关系，当推荐系统考虑的因素更多的情况下，其推荐性能将受到一定影响。而基于张量的高阶奇异值分解可在高维空间对整体数据从多个维度综合分析，挖掘数据之间潜在的语义关联，实现更加精准的推荐。

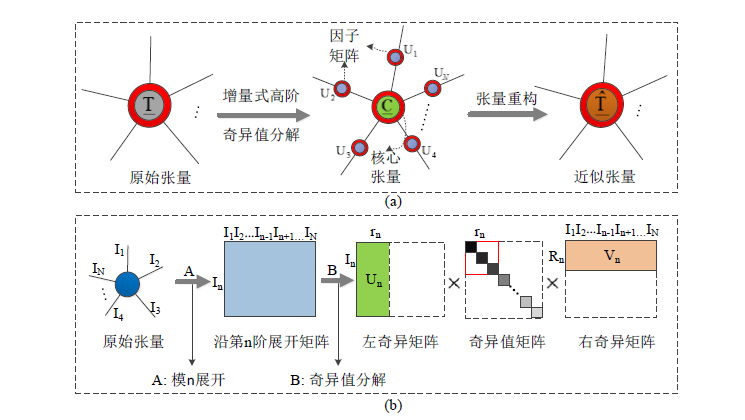
  图a可以看出，一个原始张量通过增量式高阶奇异值分解分解成了一个核心张量和多个因子矩阵的模乘，每个因子矩阵都代表当前阶上的特征矩阵；
  图b则表示可以对核心张量不重要的特征进行截取，只保留前r个关键特征（前r个奇异值）.

  大数据环境下的数据一般都是以增量方式产生，例如在学习平台上，随着新学习者的加入，融合后的全局张量将沿着学号阶进行追加。然而，当每次有新学生或者新资源加入时，每次都对更新张量重新进行高阶奇异值分解将难以实现，因为无法满足教育服务的时间要求。因此，我们采用增量是高阶奇异值分解方法来缓解其关联分析的时间。现提出基于 Jacobi旋转的增量式高阶奇异值分解算法（ Incremental HOSVD，IHOSVD）如下：

算法 8.1: 增量式高阶奇异值分解算法
输入: 原始张量 $\underline{T}\in R^{I_1\times I_2\times \cdots I_k\times \dots \times I_N}$ 的高阶奇异值分解结果 $U_n,S_n,V_n,1\le n\le N,$ 沿第
$k$ 阶进行追加的新增张量 $\underline{T}=R^{I_1\times I_2\times \dots I_k\times \dots \times I_N}$
输出：更新张量 ${\underline{T}}^{{}^{\prime }}\in R^{I_1\times I_2\times \cdots \left(I_k+I_i\right)\times \dots \times I_N}$ 的张量链格式的张量核 $U_n^{{}^{\prime \prime }},S_n^{{}^{\prime \prime }},V_n^{{}^{\prime \prime }},1\le n\le N$ 。
$1:$ (最外层)循环 for $n=1$ to $N$ 执行如下步骤
2:   对新增张量按模 $\mathrm{n}$ 展开， $T^{\prime }(n)=$Unfolding$-n(\underline{I},n)$;
3:   判断 if $\mathrm{n}=\mathrm{k}$ 处理行追加
4:      \quad 构建单位矩阵, $E_k\left(I_k\times I_k\right)$;
$5:$    初始化待正交化矩阵， $B_k^{\prime }=\left[\begin{array}{ll}{V}_k{S}_k& T_{(k)}^{\prime }\end{array}\right]$
6:      \quad 初始化 Jacobi 矩阵, $V_k^{\prime }=\left[\begin{array}{cc}{U}_k& 0\\ 0& E_k\end{array}\right]$;
7:      \quad 更新总列数, $\mathrm{c}\mathrm{o}\mathrm{l}=I_k+I_{k^{\prime }};$
8:   否则，处理列追加

9:      构建单位矩阵, $E_n\left(I_k\times I_n\right)I_{k^{\prime }}\times \left(I_k\times I_n\right)I_{k^{\prime }}$
10: \quad       初始化待正交化矩阵, $B_n=\left[\begin{array}{llc}{U}_n& S_n& T_n\end{array}\right]$
11: \quad       初始化 Jacobi 矩阵, $V_n^{\prime }=\left[\begin{array}{cc}{V}_n& 0\\ 0& E_n\end{array}\right]$;
12:      更新总列数, $col=\left(I_k\times I_n\right)\left(I_k+I_{k^{\prime }}\right)$;
13:   循环，while(未达到收敘条件)，循环执行如下步骤
14:       循环, $for{i}_n=1$ to col-1 执行
15:          循环, $for{j}_n=i_n+1$ to col 执行:
16:            判断， $if(B_n^{\prime }{\left(:,i_n\right)}^T{B}_n^{\prime }\left(:,j_n\right)$ 不满足正交性) 执行
17:               \quad 计算 Jacobi 矩阵 $J\left(i_n,j_n\right)$ 以正交第 $i_n$ 和 $j_n$ 列向量;
18:               \quad 更新矩阵 $B_n^{\prime }=B_n^{\prime }J\left(i_n,j_n\right),V_n^{\prime }=V_n^{\prime }J\left(i_n,j_n\right)$;
19: \quad 求 1 范数以归一化, ${\sigma }_n^{\prime \prime }=\left|B_n^{\prime }\left(:,i_n\right)\right|,1\le n\le col$;
20:   判断 if n=k 处理行追加
21: \quad       求左右奇异矩阵, $U_k^{\prime \prime }=V_k^{\prime };V_k^{\ast }=\left[\frac{B_k^{\prime }(:,1)}{{\sigma }_k^{\prime \prime 1}}\frac{B_k^{\prime }(:,2)}{{\sigma }_k^{\prime \prime 2}}\cdots \frac{B_k^{\prime }(:,col)}{{\sigma }_k^{\prime \prime col}}\right];$
22:   否则，处理列追加
23: \quad       求左右奇异矩阵, $V_n^{\prime \prime }=V_n^{\prime };U_n^{\prime \prime }=\left[\frac{B_n^{\prime }(:,1)}{{\sigma }_n^{\prime \prime 1}}\frac{B_n^{\prime }(:,2)}{{\sigma }_n^{\prime \prime 2}}\cdots \frac{B_n^{\prime }(:,col)}{{\sigma }_n^{\prime \prime col}}\right];$
24: \quad       求奇异矩阵, $S_n^{\prime \prime }=\mathrm{diag}\left({\sigma }_n^{"1},{\sigma }_n^{\prime \prime 2},\cdots ,{\sigma }_n^{\prime \prime col}\right)$;
25: 返回 $U_n^{\prime \prime },S_n^{\ast },V_n^{\prime \prime },1\le n\le N$ 。

3.实现不同情景下的教育资源精准推荐

  到了这一步就可以开始精准推荐了，具体流程如下：
  首先构建子张量，然后融合（并简化）；利用高阶奇异值分解并根据实际需求截断得到核心张量和因子矩阵；紧接着得到一个重构的近似张量，再对近似张量中 每个学习者在每个情景下学习过的资源的学习次数进行排序，选出前top-k个学习资源，得到资源推荐张量，类似的可以选出前top-k个学习者，得到学习者推荐张量 ，最后我们就可以借助资源推荐张量和学习者推荐张量分别为学习者推荐资源、为资源匹配学习者，从而实现精准推荐。

  对于有学习记录的学习者，通过分析学习者的学习记录，可以为学习者推荐其他的学习资源，实现基于学习行为的数据挖掘和推荐。而对于没有学习记录的新增学习者，通过学习者及资源之间的关联关系，可以为新增学习者推荐与其相似的学习者访问过的学习资源。
  现提出增量式多维关联分析的个性化推荐算法（ Incremental Tensor-based Correlative Analysis and Personalized Recommendation, ITCA-PR），这是在通过增量式高阶奇异值分解算法得到近似张量后才能够通过下面算法进行精准推荐：

接着给出一个五阶张量（表示第l 个学生在第t 个时刻的融合张量））的例子：

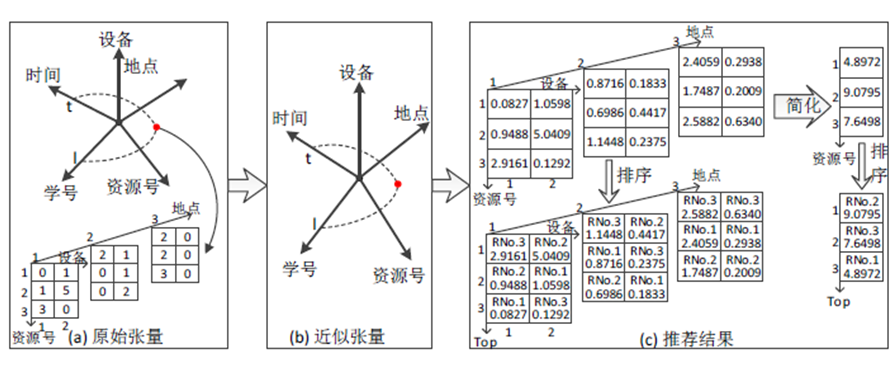
  如果不止考虑一个情景，所得推荐结果就是图c中排序后的三阶张量，如果只考虑一个情景，所得推荐结果就是图c中简化后并排序的一阶张量。
这种个性推荐算法具有以下三个特点：
第一，高阶奇异值分解的对象是融合后的整体张量，实现了对全局数据的关联分析。
第二，分解过程中去除较小的奇异值及其对应特征（通常是一些噪音数据），从而保留最主要的特征，这将有利于提高后续推荐效果。
第三，重构后得到的近似张量可以将原始张量中的零数据通过整体数据关联分析转变成非零数据，这些非零数据正好代表当前学习记录发生的相对可能性，从而挖掘原始张量中潜在的学习关联。

三.基于高阶奇异值分解的自适应聚类

  除了可以为学习者推荐资源或者为资源推荐学习者，我们还可以为学习者推荐学习者，为资源推荐资源，即为学习者找到学习伙伴或找到不同情境下自适应的资源类簇；
  论文中首先提出如何得到不同环境下的聚类张量（增量式多维关联分析的自适应聚类算法*-ITCA*），然后再基于这种算法提出如何得到指定环境下推荐的学习共同体或资源类簇（增量式自适应聚类及共同体推荐算法-ITAC-CR）
接下来就详细介绍如何实现融合张量的自适应聚类，从而构建学习共同体、找到不同情景下的资源类簇。

增量式自适应聚类的学习共同体构建

  不同的学习者在不同的情境下具有不同的学习兴趣和行为习惯，为给特定的学习者在特定的情境下推荐最合适的学习伙伴，这里提出了一种基于高阶奇异值分解的自适应聚类和学习共同体构建方法。在对张量空间的数据点进行聚类时，由于随着张量的阶数增大，张量空间的数据点会变得更加稀疏，所以要在所有数据中选择最重要的特征信息进行聚类分析。现提出一个基于增量式高阶奇异值分解的自适应聚类算法（Incremental Tensor-based Adaptive Clustering，ITAC），以在不同情境下得到自适应的聚类结果，从而构建自适应的学习共同体，其流程如图：

• 第一步，根据实际应用选择聚类对象所在的阶以及所有情境所在的阶，然后将融合张量沿着选定的阶进行矩阵展开。
• 第二步，对上述展开矩阵进行增量式奇异值分解，计算其左奇异矩阵，并通过截取较小的奇异值和对应的特征以去除噪声数据，保留主要的关键特征，而且各特征对应的特征值反应的就是特征的重要程度。基于这些关键特征进行聚类，有利于提高聚类效果。
• 第三步，将左奇异矩阵进行张量化得到聚类对象的特征张量，该张量包含所有情境下 I_n 个聚类对象的 r_n 个主要特征。
• 第四步，基于特征张量，计算在每个情境下，按照加权欧氏距离计算 I_n 个聚类对象彼此之间的相似度，得到相似度张量。
• 第五步，基于相似度张量，选择适当的聚类算法，在每个情境下对所有对象进行聚类，得到最后的聚类张量。

基于增量式高阶奇异值分解的自适应聚类算法如下：


  当某学习者进入到一个特定环境，通过该算法提供的自适应聚类张量，可以获取该情境下和该学习者属于同一类的学习者，并将他们推荐给当前学习者，从而建立自适应的学习共同体。
  基于该算法可以对学习者聚类，也可以对资源聚类从而得到指定环境下推荐的学习共同体或资源类簇，然后提出了一个增量式自适应聚类及共同体推荐算法（Incremental Tensor-based Adaptive Clustering and Community Recommendation, ITAC-CR）），具体算法如下：

  自适应的学习共同推荐有利于构建灵活高效的学习社区，自适应的资源类簇有利于资源的有效利用。

四.代码实现

  在代码实现过程中遇到了许多困难，但最难的还是在于难以充分理解原作者算法的思想，毕竟我还只是大二菜鸡一枚（其实我一直觉得自己还是大一的，毕竟有个疫情嘛）。

增量式高阶奇异值算法实现

下面的第一个代码是针对刘华中提出的增量式高阶奇异值分解算法的复现：

import torch as tc
import numpy as np
import math


# 高阶奇异值分解
def unfolding(n, t):
    t_shape = t.shape
    size = np.prod(t_shape)
    seize = size // t_shape[n - 1]
    size_list = list(range(len(t_shape)))
    size_list[0] = n - 1
    size_list[n - 1] = 0
    t = t.permute(size_list)
    return tc.reshape(t, [t_shape[n - 1], seize])


def svd(n, t):
    if n == -1:
        u, s, v = np.linalg.svd(t)
    else:
        u, s, v = np.linalg.svd(unfolding(n, t))
    u = tc.tensor(u)
    s = tc.tensor(s)
    v = tc.tensor(v)
    temp = tc.zeros([u.shape[0], v.shape[0]])
    for a in range(0, u.shape[0], 1):
        for b in range(0, v.shape[0], 1):
            if a == b:
                temp[a, b] = s[a]
    s = temp
    return u, s, v


def ho_svd(t):
    u_lis = []
    s_lis = []
    v_lis = []
    g = t
    for mi, ni in enumerate(t.shape):
        u, s, v = svd(mi + 1, t)
        u = u.double()
        s = s.double()
        v = v.double()
        u_lis.append(u)
        s_lis.append(s)
        v_lis.append(v)
        g = tc.tensordot(g, u.t(), dims=([0], [0]))
    return u_lis, s_lis, v_lis, g


# 求向量的一范数，vector表示向量
def norm1(vector):
    return np.linalg.norm(vector, ord=1)


# 求传入矩阵的一范数,n为1表示求1范数，为2表示求2范数
def norm(matrix, shape, n):
    if n == 1:
        return np.linalg.norm(matrix.reshape(1, np.prod(shape)), ord=1)
    else:
        return np.linalg.norm(matrix.reshape(1, np.prod(shape)), ord=2)


# 将奇异值向量化为奇异值矩阵
def singular_value_matrix(list_s, u, v):
    s = np.zeros((u.shape[0], v.shape[0]))
    for ni in range(0, u.shape[0], 1):
        for nj in range(0, v.shape[0], 1):
            if ni == nj:
                s[ni, nj] = list_s[ni]
    return tc.tensor(s)


# u_lis, s_lis, v_lis为传入的左右奇异矩阵列表和奇异值矩阵列表，shape_1, shape_2为原张量和新张量的形状
# k1为要增量的阶，t为新增张量
def high_ho_svd(u_lis, s_lis, v_lis, k1, t):
    for n in range(1, len(u_lis) + 1, 1):
        # singular_value存奇异值
        singular_value = []
        # 矩阵tt是n-模展开的矩阵
        tt = unfolding(n, t)
        # 处理行追加
        if n == k1:
            orthogonal_matrix = tc.cat((s_lis[k1-1] @ v_lis[k1-1], tt), 0)
            orthogonal_matrix_col = orthogonal_matrix.shape[1]
            e = np.identity(orthogonal_matrix_col - u_lis[k1-1].shape[0])
            e = tc.tensor(e)
            v1 = tc.cat((u_lis[k1-1], tc.zeros([u_lis[k1-1].shape[0], e.shape[1]])), 1)
            v2 = tc.cat((tc.zeros([e.shape[0], u_lis[k1-1].shape[1]]), e), 1)
            v = tc.cat((v1, v2), 0)
            col = v.shape[0]
        # 处理列追加
        else:
            orthogonal_matrix = tc.cat((u_lis[n-1] @ s_lis[n-1], tt), 1)
            orthogonal_matrix_col = orthogonal_matrix.shape[1]
            e = np.identity(orthogonal_matrix_col - v_lis[n - 1].shape[0])
            e = tc.tensor(e)
            v1 = tc.cat((v_lis[n - 1], tc.zeros([v_lis[n - 1].shape[0], e.shape[1]])), 1)
            v2 = tc.cat((tc.zeros([e.shape[0], v_lis[n - 1].shape[1]]), e), 1)
            v = tc.cat((v1, v2), 0)
            col = v.shape[1]
        # 收敛条件为更新的待正交矩阵orthogonal_matrix对角线上的元素的二范数与整个矩阵的二范数的比值达到一个阈值
        singular_value_norm1 = 0.96
        matrix_norm2 = 1
        count = 0
        while 1 - (singular_value_norm1 / matrix_norm2) < 0.05:
            for ni in range(0, col, 1):
                for nj in range(ni, col, 1):
                    if orthogonal_matrix[:, ni] @ orthogonal_matrix[:, nj] != 0 & ni != nj:
                        jaco = jacobi(orthogonal_matrix, orthogonal_matrix_col, ni, nj)
                        orthogonal_matrix = orthogonal_matrix @ jaco
                        v = v @ jaco
                        singular_value_norm1 = norm1(find_vector(orthogonal_matrix))
                        matrix_norm2 = norm(orthogonal_matrix, orthogonal_matrix.shape, 2)
                        count += 1
                    else:
                        continue
        # 得到奇异值列表
        for ni in range(0, col, 1):
            singular_value.append(norm1(orthogonal_matrix[:, ni]))
        # 对正交矩阵和奇异值列表进行排序
        for ni in range(0, col-1, 1):
            for nj in range(ni, col, 1):
                if singular_value[ni] < singular_value[nj]:
                    temp = singular_value[ni]
                    singular_value[ni] = singular_value[nj]
                    singular_value[nj] = temp
                    temp1 = orthogonal_matrix[:, ni]
                    orthogonal_matrix[:, ni] = orthogonal_matrix[:, nj]
                    orthogonal_matrix[:, nj] = temp1
        # 求左右奇异矩阵
        if n == k1:
            u_lis[k1 - 1] = v[0:orthogonal_matrix.shape[0], 0:orthogonal_matrix.shape[0]]
            v = tc.zeros(orthogonal_matrix.shape)
            for count in range(0, col, 1):
                if singular_value[count] != 0:
                    v[:, count] = orthogonal_matrix[:, count]/singular_value[count]
            v_lis[k1 - 1] = v
            s_lis[n - 1] = singular_value_matrix(singular_value, u_lis[k1 - 1], v)
        else:
            v_lis[n - 1] = v
            u = tc.zeros(orthogonal_matrix.shape)
            for count in range(0, col, 1):
                if singular_value[count] != 0:
                    u[:, count] = orthogonal_matrix[:, count]/singular_value[count]
            u_lis[n-1] = u[0:orthogonal_matrix.shape[0]:, 0:orthogonal_matrix.shape[0]]
            s_lis[n - 1] = singular_value_matrix(singular_value, u[:, 0:orthogonal_matrix.shape[0]], v)
    return u_lis, s_lis, v_lis


# 雅克比方法,最后需要返回一个雅克比矩阵j
def jacobi(orthogonal_matrix, orthogonal_matrix_col, ni, nj):
    jaco = np.identity(orthogonal_matrix_col)
    expanded_orthogonal_matrix = expand_orthogonal_matrix(orthogonal_matrix)
    aii = expanded_orthogonal_matrix[ni, ni]
    ajj = expanded_orthogonal_matrix[nj, nj]
    aij = expanded_orthogonal_matrix[ni, nj]
    if aii - ajj == 0:
        theta = 3.1416 / 4
        jaco[ni, ni] = math.cos(theta)
        jaco[nj, nj] = math.cos(theta)
        jaco[ni, nj] = -math.sin(theta)
        jaco[nj, ni] = math.sin(theta)
    else:
        theta = math.atan(2*aij / (aii - ajj))/2
        jaco[ni, ni] = math.cos(theta)
        jaco[nj, nj] = math.cos(theta)
        jaco[ni, nj] = -math.sin(theta)
        jaco[nj, ni] = math.sin(theta)
    return jaco


# 按行进行维度扩展，扩展部分元素全为0
def expand_orthogonal_matrix(orthogonal_matrix):
    row = orthogonal_matrix.shape[1]-orthogonal_matrix.shape[0]
    col = orthogonal_matrix.shape[1]
    e = tc.zeros((row, col))
    return tc.cat((orthogonal_matrix, e), 0)


# 把矩阵对角线上的元素单独化为一个向量
def find_vector(orthogonal_matrix):
    dia_element = []
    for ni in range(0, orthogonal_matrix.shape[0], 1):
        for nj in range(0, orthogonal_matrix.shape[1], 1):
            if ni == nj:
                dia_element.append(orthogonal_matrix[ni, ni])
    return dia_element


# 计算欧氏距离
def euclidean_distance(t1, t2):
    t3 = t1 - t2
    return norm(t3, t3.shape, 2)


if __name__ == '__main__':
    # 原张量
    tensor1 = tc.randint(0, 10, [2, 2, 4]).double()
    # 新增张量
    tensor2 = tc.randint(0, 10, [2, 3, 4]).double()
    # k为要增量的阶
    k = 2
    # 对原始张量作高阶奇异值分解
    u_list, s_list, v_list, gg = ho_svd(tensor1)
    u_list2, s_list2, v_list2 = high_ho_svd(u_list, s_list, v_list, k, tensor2)
    # T为直接合并的新张量，u_list2、s_list2、v_list2存增量式高阶奇异值的分解结果，u_list1、s_list、v_list、gg1存直接对新张量进行高阶奇异值分解的结果
    T = tc.cat((tensor1, tensor2), k - 1)
    u_list1, s_list1, v_list1, gg1 = ho_svd(T)
    gg2 = tc.ones(T.shape)
    gg2.copy_(T)
    for i in range(0, len(u_list), 1):
        gg2 = tc.tensordot(gg2, u_list2[i].t().float(), dims=([0], [0]))
    print("**********************")
    print("增量式高阶奇异值分解u1", u_list2[0])
    print("直接高阶奇异值分解u1", u_list1[0])
    print("**********************")
    print("增量式高阶奇异值分解u2", u_list2[1])
    print("直接高阶奇异值分解u2", u_list1[1])
    print("**********************")
    print("增量式高阶奇异值分解u3", u_list2[2])
    print("直接高阶奇异值分解u3", u_list1[2])
    print("**********************")
    print("两个核心张量的欧氏距离为：", euclidean_distance(gg1, gg2))
    print("增量式高阶奇异值分解得到的核心张量相对高阶奇异值分解得到的核心张量的相对误差",
          euclidean_distance(gg1, gg2) / norm(gg1, gg1.shape, 2))

  这两个代码先保存在这，应该还存在错误的地方，具体的讲解下次再找时间写一写。

  本博客整理自华中科技大学刘华中的博士学位论文——《基于张量的大数据高效计算及多模态分析方法研究》的第八章基于高阶奇异值的多模态推荐和聚类方法