1.6 状态压缩DP

1. 棋盘问题

1.1 蒙德里安的梦想

将一种状态用二进制来表示。

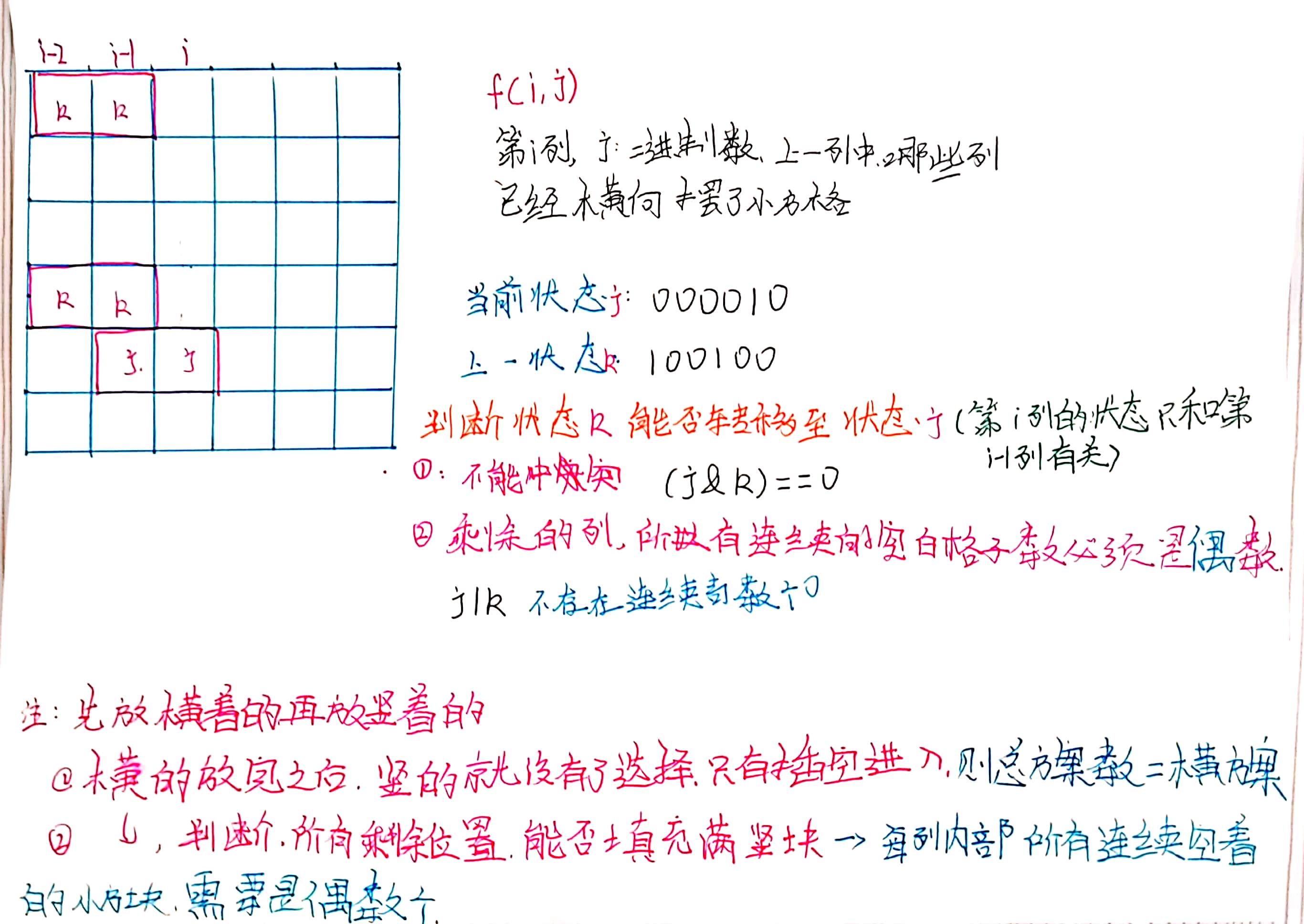
1. 对于此题，由于小方块是1*2，如果先摆放横着的，

   故在摆放第i列时，只需要考虑第i-1列有没有冲突的。

2. 然后在插空摆放竖着的，如果横向摆放已经确定，

   那么竖向的也是确定的，即：总方案数 = 横向摆放的方案数。

3. 要判断摆放是否合法，即不能有空余的小方块。

   那么：在摆放第i列竖向的时候，需要判断，第i列中的数个连续的的空白位置，

   是否是偶数个( 偶数个才能正好将竖向的方块摆满)。

对于一列来说，共有$2^N$个状态的可能。

对于i列是否与i-1列冲突，j&k == 0 （k为第i-1列的状态(确定合法)，j为第i列的状态(不确定是否合法)）

对于判断某一个状态中的空白位置是否是偶数个，预处理即可——遍历$2^N$个状态，将每种状态是否可行，放到dp中（只是一个标记数组），j|k 是第i列 和第i-1列合起来之后的状态，看这个状态的空白位置是否合法。

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int n = 12, m = 1 << n; // 一位代表当前行的状态 所以要1 << n 个状态
int N, M;
long long f[n][m];
bool dp[m]; // 标记此状态下空余的格子数是否是偶数个 偶数个就可以竖着放
int main()
{
    while (cin >> N >> M, N || M)
    {
        // 一共有这些个状态 2^n
        for (int i = 0; i < 1 << N; i++)
        {
            int cnt = 0;
            dp[i] = true;
            for (int j = 0; j < N; j++)
                if ((i >> j) & 1) // 遍历此状态的每一位
                {
                    // 状态i不可取
                    if(cnt % 2 == 1)    
                    {
                        dp[i] = false;
                        break;
                    }
                    cnt = 0;
                }
                else
                    cnt++;
            // 最后一个
            if (cnt % 2 == 1)
                dp[i] = false;
        }
        memset(f, 0, sizeof f);
        f[0][0] = 1;
        // M列
        for (int i = 1; i <= M; i++)
            //            枚举i列每一种状态
            for (int j = 0; j < 1 << N; j++)
                //                枚举i-1列每一种状态
                for (int k = 0; k < 1 << N; k++)
                    if ((j & k) == 0 && dp[j | k])
                        f[i][j] += f[i - 1][k]; //那么这种状态下它的方案数等于之前每种k状态数目的和
        cout << f[M][0] << endl;
    }
    return 0;
}