这是我参与8月更文挑战的第7天，活动详情查看：8月更文挑战。

原文地址：Simplest artificial neural network

原文作者：Givi Odikadze（已授权）

译者 & 校正：HelloGitHub-小熊熊 & 卤蛋

导言

我不会机器学习，但上个月我在 GitHub 上发现了一个极简、入门级的神经网络教程。它简洁易懂能用一行公式说明白的道理，不多写一句废话，我看后大呼过瘾。

这么好的东西得让更多人看到，但原文是英文的无法直接分享，所以得先联系作者拿到翻译的授权，然后由小熊熊翻译了这个项目，最后才有您看到的这篇文章。过程艰辛耗时一个月实属不易，如果您看完觉得还不错，欢迎点赞、分享给更多人。

内容分为两部分：

第一部分：最简单的人工神经网络
第二部分：最基础的反向传播算法

人工神经网络是人工智能的基础，只有夯实基础，才能玩转 AI 魔法！

温馨提示：公式虽多但只是看起来唬人，实际耐下心读并不难懂。下面正文开始！

一、最简单的人工神经网络

通过理论和代码解释和演示的最简单的人工神经网络。

示例代码：github.com/gokadin/ai-…

理论

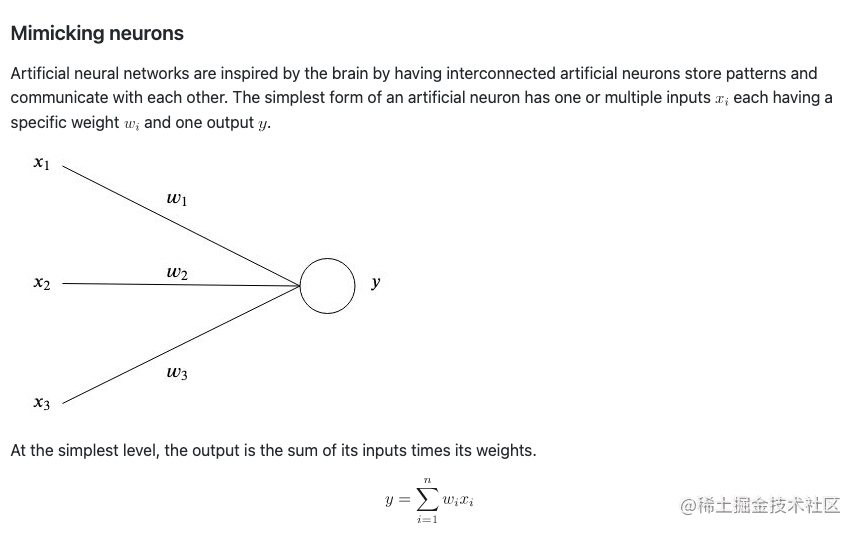
模拟神经元

受人脑工作机制的启发，人工神经网络有着相互连接的模拟神经元，用于存储模式和相互沟通。一个模拟神经元最简单的形式是有一个或多个输入值 $x_i$ 和一个输出值 $y$ ，其中每个 $x_i$ 有一个权重 $w_i$ 。

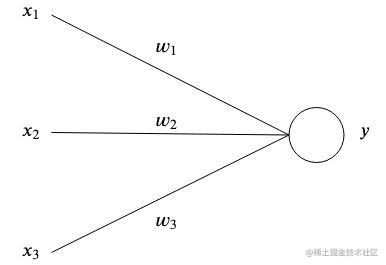
拿最简单的来说，输出值就是输入值乘以权重之后的总和。

y = \sum_{i=1}^{n}{w_i}{x_i}

一个简单的例子

网络的作用在于通过多个参数 $w$ 模拟一个复杂的函数，从而可以在给定一系列输入值 $x$ 的时候得到一个特定的输出值 $y$ ，而这些参数 $w$ 通常是我们自身难以拟定的。

假设我们现在的一个网络有两个输入值 $x_1 = 0.2$ ， $x_2 = 0.4$ ，它们对应两个权重值 $w_1$ 和 $w_2$ 。

现在我们需要调整权重值，从而使得它们可以产生我们预设的输出值。

在初始化时，因为我们不知晓最优值，往往是对权重随机赋值，这里我们为了简单，将它们都初始化为 1 。

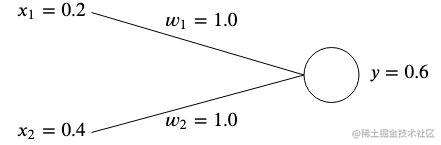
这种情况下，我们得到的就是

y = x_1w_1 + x_2w_2 = 0.2 * 1 + 0.4 * 1 = 0.6

误差值

如果输出值 $y$ 与我们期望的输出值不一致，那就有了误差。

例如，如果我们希望目标值是 $t = 0.5$ ，那么这里相差值就是

y - t = 0.6 - 0.5 = 0.1

通常我们会采用方差（也就是代价函数）来衡量误差：

E = \frac{1}{2}(y - t)^2

如果有多套输入输出值，那么误差就是每组方差的平均值。

E = \frac{1}{2n}(y_i - t_i)^2

我们用方差来衡量得到的输出值与我们期望的目标值之间的差距。通过平方的形式就可以去除负偏离值的影响，更加凸显那些偏离较大的偏差值（不管正负）。

为了纠正误差，我们需要调整权重值，以使得结果趋近于我们的目标值。在我们这个例子中，将 $w_1$ 从 1.0 降到 0.5 就可以达到目标，因为

y = t = 0.2 * 0.5 + 0.4 * 1.0 = 0.5

然而，神经网络往往涉及到许多不同的输入和输出值，这种情况下我们就需要一个学习算法来帮我们自动完成这一步。

梯度下降

现在是要借助误差来帮我们找到应该被调整的权重值，从而使得误差最小化。但在这之前，让我们了解一下梯度的概念。

什么是梯度？

梯度本质上是指向一个函数最大斜率的矢量。我们采用 ${\triangledown}$ 来表示梯度，简单说来，它就是函数变量偏导数的矢量形式。

对于一个双变量函数，它采用如下形式表示：

\triangledown f(x,y) = \left[f_x, f_y\right] = \left[\frac{\eth f(x,y)}{\eth_x},\frac{\eth f(x,y)}{\eth_y}\right]

让我们用一些数字来模拟一个简单的例子。假设我们有一个函数是 $f(x,y) = 2x^2 + 3y^3$ ，那么梯度将是

\triangledown f(x,y) = [4x, 9y^2]

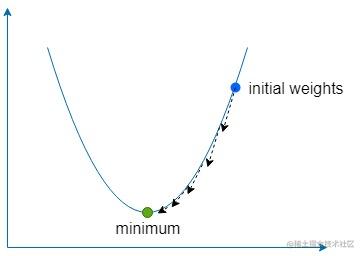
什么是梯度下降？

下降则可以简单理解为通过梯度来找到我们函数最大斜率的方向，然后通过反方向小步幅的多次尝试，从而找到使函数全局（有时是局部）误差值最小的权重。

我们采用一个称为学习率的常量来表示这个反方向的小步幅，在公式中我们用 $\varepsilon$ 来进行表征。

如果 $\varepsilon$ 取值太大，那有可能直接错过最小值，但如果取值太小，那我们的网络就会花费更久的时间来学习，而且也有可能陷入一个浅局部最小值。

对于我们例子中的两个权重值 $w_1$ 和 $w_2$ ，我们需要找到这两个权重值相较于误差函数的梯度

\triangledown_wE = <\frac{\eth_E}{\eth_{w_1}},\frac{\eth_E}{\eth_{w_2}}>

还记得我们上面的公式 $E = \frac{1}{2}(y - t)^2$ 和 $y = x_1w_1 + x_2w_2$ 吗？对于 $w_1$ 和 $w_2$ ，我们可以将其带入并通过微积分中的链式求导法则来分别计算其梯度

\frac{\eth_E}{\eth_{w_i}} = \frac{\eth_E}{\eth_{y}}\frac{\eth_y}{\eth_{w_i}}=\frac{\eth}{\eth_{y}}(\frac{1}{2}(y-t)^2)\frac{\eth}{\eth_{w_i}}(x_iw_i) = (y - t)x_i

简洁起见，后面我们将采用 $\delta$ 这个术语来表示 $\frac{\eth_E}{\eth_{y}} = y - t$ 。

一旦我们有了梯度，将我们拟定的学习率 $\varepsilon$ 带入，可以通过如下方式来更新权重值：

w_1 = w_1 - \varepsilon \triangledown_{w_1}E = w_1 - \varepsilon \delta{x_1}

w_2 = w_2 - \varepsilon \triangledown_{w_2}E = w_2 - \varepsilon \delta{x_2}

然后重复这个过程，直到误差值最小并趋近于零。

代码示例

附带的示例采用梯度下降法，将如下数据集训练成有两个输入值和一个输出值的神经网络：

x = \left[ \begin{matrix} 1.0 & 1.0 \\ 1.0 & 0.0 \end{matrix} \right] \quad y{'}= [ 0.0\quad 1.0 ]

一旦训练成功，这个网络将会在输入两个 1 时输出 ~0，在输入 1 和 0 时，输出 ~1 。

怎么运行？

Go

PS D:\github\ai-simplest-network-master\src> go build -o bin/test.exe
PS D:\github\ai-simplest-network-master\bin> ./test.exe

err:  1.7930306267024234
err:  1.1763080417089242
……
err:  0.00011642621631266815
err:  0.00010770190838306002
err:  9.963134967988221e-05
Finished after 111 iterations

Results ----------------------
[1 1] => [0.007421243532258703]
[1 0] => [0.9879921757260246]

复制代码

Docker

docker build -t simplest-network .
docker run --rm simplest-network
复制代码

二、最基础的反向传播算法

反向传播（英语：Backpropagation，缩写为 BP）是“误差反向传播”的简称，是一种与最优化方法（如梯度下降法）结合使用的，用来训练人工神经网络的常见方法。

反向传播技术可以用来训练至少有一个隐藏层的神经网络。下面就来从理论出发结合代码拿下反向传播算法。

示例代码：github.com/gokadin/ai-…

理论

感知机介绍

感知机是这样一个处理单元：它接受输入 $x$ , 采用激活函数 $f$ 对其进行转换，并输出结果 $y$ 。

在一个神经网络，输入值是前一层节点输出值的权重加成总和，再加上前一层的误差：

x_j = \sum_{i=1}^{I}{x_i}{w_{ij}} + b_i

如果我们把误差当作层中另外的一个常量为 -1 的节点，那么我们可以简化这个公式为

x_j = \sum_{i=1}^{I+1}{x_i}{w_{ij}}

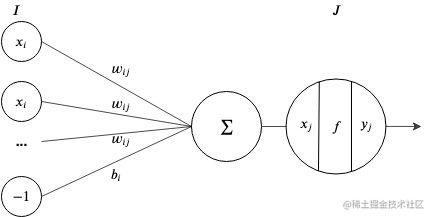
激活函数

为什么我们需要激活函数呢？如果没有，我们每个节点的输出都会是线性的，从而让整个神经网络都会是基于输入值的一个线性运算后的输出。因为线性函数组合仍然是线性的，所以必须要引入非线性函数，才能让神经网络有区别于线性回归模型。

针对 $x=\sum{\vec x}{\vec w}$ ，典型的激活函数有以下形式：

Sigmoid 函数 : $y = \frac {1} {1+e^{-x}}$

线性整流函数： $y = max(0,x)$

tanh 函数： $y = tanh(x)$

反向传播

反向传播算法可以用来训练人工神经网络，特别是针对具有多于两层的网络。

原理是采用 forward pass 来计算网络输出值和误差，再根据误差梯度反向更新输入层的权重值。

术语

$x_i, x_j, x_k$ 分别是 I, J, K 层节点的输入值。
$y_i, y_j, y_k$ 分别是 I, J, K 层节点的输出值。
$y^{'}_{k}$ 是 K 输出节点的期望输出值。
$w_{ij}, w_{jk}$ 分别是 I 到 J 层和 J 到 K 层的权重值。
$t$ 代表 T 组关联中当前的一组关联。

在下面的示例中，我们将对不同层节点采用以下激活函数：

输入层 -> 恒等函数
隐藏层 -> Sigmoid 函数
输出层 -> 恒等函数

The forward pass

在 forward pass 中，我们在输入层进行输入，在输出层得到结果。

对于隐藏层的每个节点的输入就是输入层输入值的加权总和：

x_j = \sum_{i=1}^{I}{w_{ij}}{y_i}

因为隐藏层的激活函数是 sigmoid，那么输出将会是：

y_j = f_j(x_j) = \frac {1}{1 + e^{-x_j}}

同样，输出层的输入值则是

x_k = \sum_{j=1}^{J}{w_{jk}}{y_j}

因为我们赋予了恒等函数做为激活函数，所以这一层的输出将等同于输入值。

y_k = f_k(x_k) = x_k

一旦输入值通过网络进行传播，我们就可以计算出误差值。如果有多套关联，还记得我们第一部分学习的方差吗？这里，我们就可以采用平均方差来计算误差。

E = \sum_{i=1}^{I}{E_{t}}=\frac{1}{2T}\sum_{t=1}^{T}({y_{kt}} - {y^{'}_{kt}})^2

The backward pass

现在我们已经得到了误差，就可以通过反向传输，来用误差来修正网络的权重值。

通过第一部分的学习，我们知道对权重的调整可以基于误差对权重的偏导数乘以学习率，即如下形式

\Delta w_{jk} = - \varepsilon \frac{\partial E}{\partial w_{jk}}

我们通过链式法则计算出误差梯度，如下：

\frac{\partial E}{\partial w_{jk}} = \frac{\partial E}{\partial x_{k}}\frac{\partial x_k}{\partial w_{jk}}

\frac{\partial E}{\partial x_{k}} = \frac{\partial E}{\partial y_{k}} \frac{\partial y_k}{\partial x_{k}} = \frac{\partial}{\partial y_{k}}(\frac{1}{2}(y_k - y^{'}_k)^2)\frac{\partial}{\partial x_k}(x_k) = y_k - y^{'}_k = \delta_k

\frac{\partial x_k}{\partial w_{jk}} = \frac{\partial}{\partial w_{jk}}(y_jw_{jk}) = y_j

因此，对权重的调整即为 $\Delta w_{jk} = - \varepsilon \delta_k y_j$

对于多个关联，那么对权重的调整将为每个关联的权重调整值之和 $\Delta w_{jk} = - \varepsilon \sum_{t=1}^{T}\delta_k y_{jt}$

类似地，对于隐藏层之间的权重调整，继续以上面的例子为例，输入层和第一个隐藏层之间的权重调整值为

\Delta w_{ij} = - \varepsilon \frac{\partial E}{\partial w_{ij}}

\frac{\partial E}{\partial w_{ij}} = \frac{\partial E}{\partial x_{j}}\frac{\partial x_j}{\partial w_{ij}} = \delta_jy_i

那么，基于所有关联的权重调整即为每次关联计算得到的调整值之和 $\Delta w_{ij} = - \varepsilon \sum_{t=1}^{T}\delta_{jt}y_{it}$

$\delta_j$ 计算

这里，我们对 $\delta_j$ 可以再做进一步的探索。上文中，我们看到 $\frac{\partial E}{\partial w_{ij}} = \frac{\partial E}{\partial x_{j}}\frac{\partial x_j}{\partial w_{ij}}$ 。

对前半部分的 $\frac{\partial E}{\partial x_{j}}$ ，我们可以有

\frac{\partial E}{\partial x_{j}} = \frac{\partial E}{\partial y_{j}}\frac{d_{y_j}}{d_{x_j}}

\frac{\partial E}{\partial y_j} = \sum_{k=1}^K \frac {\partial E}{\partial x_k}\frac {\partial x_k}{\partial y_j} = \sum_{k=1}^K \delta_k w_{jk}

对后半部分的 $\frac{d_{y_j}}{d_{x_j}}$ ，因为我们在这一层采用了 sigmoid 函数，我们知道，sigmoid 函数的导数形式是 $f(x)(1-f(x))$ ，因此，有

\frac{d_{y_j}}{d_{x_j}} = f^{'}(x_j) = f(x_j)(1-f(x_j)) = y_j(1-y_j)

综上，便可以得到 $\delta_j$ 的计算公式如下

\delta_j = y_j(1-y_j)\sum_{k=1}^K \delta_k w_{jk}

算法总结

首先，对网络权重值赋予一个小的随机值。

重复以下步骤，直到误差为0 ：

对每次关联，通过神经网络向前传输，得到输出值
- 计算每个输出节点的误差（ $\delta_k = y_k - y^{'}_k$ ）
- 叠加计算每个输出权重的梯度（ $\triangledown_{w_{jk}}E = \delta_k y_j$ ）
- 计算隐藏层每个节点的 $\delta$ （ $\delta_j = y_j(1-y_j)\sum_{k=1}^K \delta_k w_{jk}$ ）
- 叠加计算每个隐藏层权重的梯度（ $\triangledown_{w_{ij}}E = \delta_j y_j$ ）
更新所有权重值，重置叠加梯度（ $w = w - \varepsilon\triangledown E$ ）

图解反向传播

在这个示例中，我们通过真实数据来模拟神经网络中的每个步骤。输入值是[1.0, 1.0]，输出期望值为 [0.5]。为了简化，我们将初始化权重设为 0.5 （虽然在实际操作中，经常会采用随机值）。对于输入、隐藏和输出层，我们分别采用恒等函数、 sigmoid 函数和恒等函数作为激活函数，学习率 $\varepsilon$ 则定为 0.01 。

Forward pass

运算一开始，我们将输入层的节点输入值设为 $x_1 = 1.0, x_2 = 1.0$ 。

因为我们对输入层采用的是恒等函数作为激活函数，因此有 $y_i = x_i = 1.0$ 。

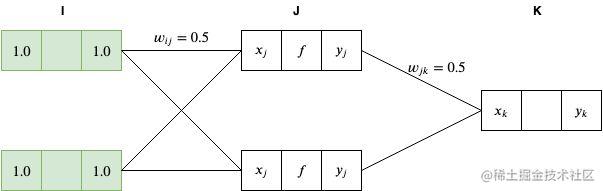
接下来，我们通过对前一层的加权总和将网络向前传递到 J 层，如下

x_j = \sum_{i=1}^Iy_iw_{ij}= 1.0*0.5+1.0*0.5=1.0

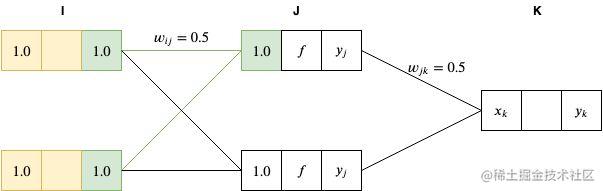
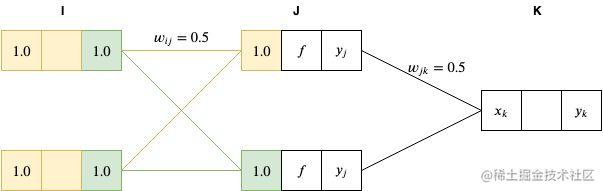
然后，我们将 J 层节点的值输入到 sigmoid 函数（ $f(x)=\frac{1}{1+e^{-x}}$ ，将 $x=1$ 代入，得到 0.731）进行激活。

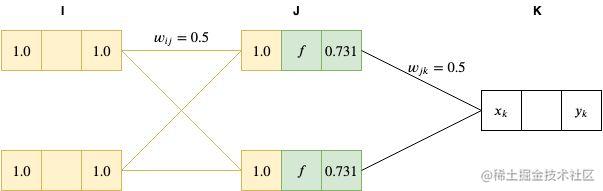
最后，我们将这个结果传递到最后的输出层。

x_k = 0.731*0.5+0.731*0.5 = 0.731

因为我们输出层的激活函数也是恒等函数，因此 $y_k = x_k = 0.731$

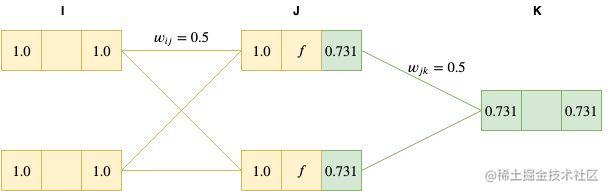
Backward pass

反向传播的第一步，是计算输出节点的 $\delta$ ，

\delta_k = y_k - y'_k = 0.731-0.5=0.231

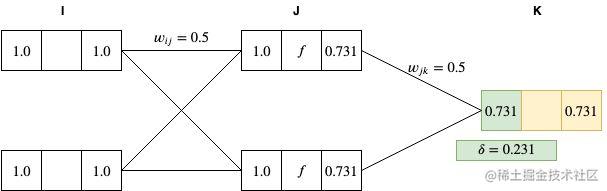
采用 $\delta$ 计算 J 和 K 两层节点间的权重梯度： $\triangledown_{w_{jk}}E = \delta_ky_j=0.231*0.731=0.168861$

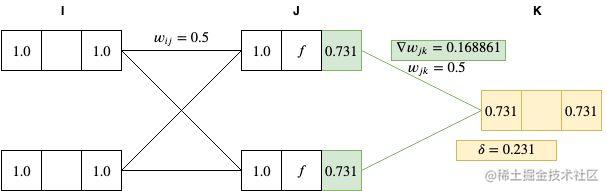
接下来，以同样的方法计算每个隐藏层的 $\delta$ 值（在本示例中，仅有一个隐藏层）：

\delta_j = y_j(1-y_j)\sum_{k=1}^K\delta_kw_{jk}=0.731*(1-0.731)*(0.5*0.231)\approx0.0227

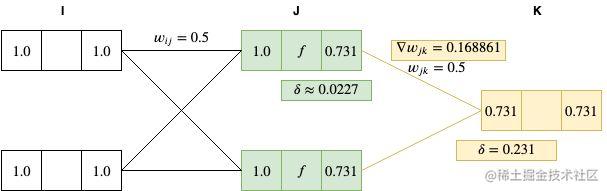
针对 I 和 J 层节点权重计算其梯度为：

\triangledown_{w_{ij}}E=\delta_jy_i = 0.0227*1=0.0227

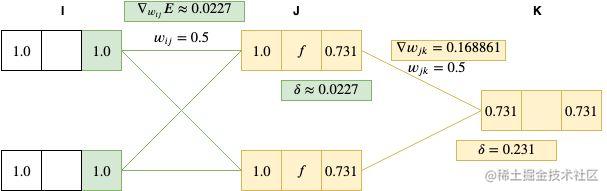
最后一步是用计算出的梯度更新所有的权重值。注意这里如果我们有多于一个的关联，那么便可以针对每组关联的梯度进行累计，然后更新权重值。

w_{ij}=w_{ij}-\varepsilon\triangledown_{w_{ij}}E=0.5-0.01*0.0227=0.499773

w_{jk}=w_{jk}-\varepsilon\triangledown_{w_{jk}}E=0.5-0.01*0.168861=0.49831139

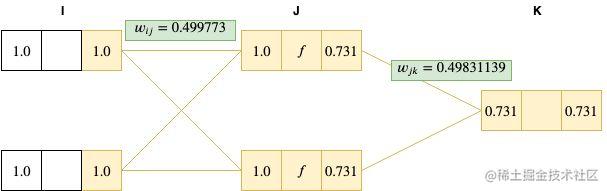
可以看到这个权重值变化很小，但如果我们用这个权重再跑一遍 forward pass，一般来说将会得到一个比之前更小的误差。让我们现在来看下……

第一遍我们得到的 $y_1 = 0.731$ ，采用新的权重值计算得到 $y_2\approx0.7285$ 。

由此， $y_1-y'_1=0.231$ ，而 $y_2-y'_2=0.2285$ 。

可见，误差得到了减小！尽管减少值很小，但对于一个真实场景也是很有代表性的。按照该算法重复运行，一般就可以将误差最终减小到0，那么便完成了对神经网络的训练。

代码示例

本示例中，将一个 2X2X1 的网络训练出 XOR 运算符的效果。

x= \left[ \begin{matrix} 1.0 & 1.0 & 0.0 & 0.0 \\ 1.0 & 0.0 & 1.0 & 0.0 \end{matrix} \right]

y'= \left[ \begin{matrix} 0.0 & 1.0 & 1.0 & 0.0 \end{matrix} \right]

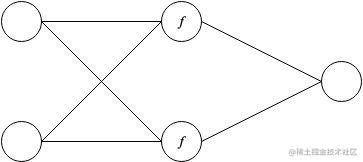
这里，f 是针对隐藏层的 sigmoid 激活函数。

注意，XOR 运算符是不能通过第一部分中的线性网络进行模拟的，因为数据集分布是非线性的。也就是你不能通过一条直线将 XOR 的四个输入值正确划分到两类中。如果我们将 sigmoid 函数换为恒等函数，这个网络也将是不可行的。

讲完这么多，轮到你自己来动手操作啦！试试采用不同的激活函数、学习率和网络拓扑，看看效果如何？

最后

恭喜看完本文！你学会了吗？

关注 HelloGitHub 公众号第一时间收到更新。

还有更多开源项目的介绍和宝藏项目等待你的发现。

最简单的人工神经网络

导言

一、最简单的人工神经网络

理论

模拟神经元

一个简单的例子

误差值

梯度下降

什么是梯度？

什么是梯度下降？

代码示例

怎么运行？

Go

Docker

二、最基础的反向传播算法

理论

感知机介绍

激活函数

反向传播

术语

The forward pass

The backward pass

δ j \delta_j δj​ 计算

算法总结

图解反向传播

Forward pass

Backward pass

代码示例

最后

猜你喜欢

$\delta_j$ 计算