文章目录
本系列博客用于记录学习浙江大学陈越、何钦铭老师的数据结构基础,课程链接为:数据结构基础—陈越、何钦铭
一、什么是数据结构
数据结构没有一个明确的定义,我们先看看一些人对数据结构的定义。
1、数据结构是数据对象,以及存在于该对象的实例和组成实例的数据元素之间的各种联系。这些联系可以通过定义相关的函数来给出。
——Sartaj Sahni,《数据结构、算法与应用》
2、数据结构是ADT(抽象数据类型Abstract Data Type)的物理实现。
——Clifford A.Shaffer,《数据结构与算法分析》
3、数据结构(data structure)是计算机中存储、组织数据的方式。通常情况下,精心选择的数据结构可以带来最优效率的算法。
——中文维基百科
那么到底要怎么定义数据结构这个东西呢?我想一句话两句话是讲不清楚的。不如我来给你讲三个例子
1.1 关于数据组织
例1:如何在书架上摆放图书?也就是说,我给了你一些书架,然后又有一堆书进来你要把它们怎么放到书架上去呢?换言之说我给了你一堆数据,然后给了你一些存储空间你要怎么把这些数据存起来呢?
图书的摆放要使得2个相关操作方便实现:
操作1:新书怎么插入?
操作2:怎么找到某本指定的书?
方法1:随便放
• 操作1:新书怎么插入?
• 哪里有空放哪里,一步到位!
• 操作2:怎么找到某本指定的书?
• 累死,需要把所有书过一遍
方法2:按照书名的拼音字母顺序排放
• 操作1:新书怎么插入?
• 效率低,如果新进一本《阿Q正传》,需要把几乎所有书往后挪动。
• 操作2:怎么找到某本指定的书?
• 根据拼音字母进行二分查找!查找次数比第一次少得多。
方法3:把书架划分成几块区域,每块区域指定摆放某种类别的图书;在每种类别内,按照书名的拼音字母顺序排放
• 操作1:新书怎么插入?
• 先定类别,二分查找确定位置,移出空位
• 操作2:怎么找到某本指定的书?
• 先定类别,再二分查找
• 问题:空间如何分配?类别应该分多细?
根据这个例子我们可以知道:解决问题方法的效率,跟数据的组织方式有关
1.2 关于空间使用
例2:写程序实现一个函数PrintN,使得传入一个正整数为N的参数后,能顺序打印从1到N的全部正整数。
循环实现:
void PrintN(int N)
{
int i;
for (i = 1; i <= N; i++) {
printf("%d\n", i);
}
return;
}
递归实现:
void PrintN ( int N )
{
if ( N ){
PrintN( N - 1 );
printf("%d\n", N );
}
return;
}
我们来测试一下。首先是输入1000,两种方法结果如下。可以看出结果一模一样。

如果输入100000呢?循环实现仍然正常输出结果,但是递归实现直接报错:栈溢出。

到底发生了什么呢?我们后面会仔细地来讲。在这儿我们主要说的是,虽然递归的代码看上去非常地简洁且容易理解。但是,你的计算机特别不愿意跑递归的程序,因为递归的程序对空间的占用有的时候可能是很恐怖的。比如说我们这道题,递归的那个函数把它能用的空间全部吃掉,还不够吃,然后它就爆掉了。所以它还来不及打出任何一个数字就非正常终止,跳出了。
这个故事告诉我们的是:解决问题方法的效率,也跟空间的利用效率是有关的
1.3 关于算法效率
例3:写程序计算给定多项式在给定点x处的值。
普通方法: f ( x ) = a 0 + a 1 x + . . . + a n − 1 x n − 1 + a n x n f(x) = {a_0} + {a_1}x + ... + {a_{n - 1}}{x^{n - 1}} + {a_n}{x^n} f(x)=a0+a1x+...+an−1xn−1+anxn
//n是这个多项式的阶数
//多项式的系数放在数组a[]里面
//x是我们要计算的这个点
double f(int n, double a[], double x)
{
int i;
double p = a[0];
for (i = 1; i <= n; i++)
p += (a[i] * pow(x, i));
return p;
}
巧妙使用结合律: f ( x ) = a 0 + x ( a 1 + x ( . . . ( a n − 1 + x ( a n ) ) . . . ) ) f(x) = {a_0} + x({a_1} + x(...({a_{n - 1}} + x({a_n}))...)) f(x)=a0+x(a1+x(...(an−1+x(an))...))
double f( int n, double a[], double x )
{
int i;
double p = a[n];
for ( i=n; i>0; i-- )
p = a[i-1] + x*p;
return p;
}
然而第一个函数比第二个函数要慢很多,我们来实际测一下。C语言提供了一个函数clock,可以捕捉从程序开始运行一直到这个函数被调用那个时刻所耗费的时间。这个时间的单位是clock tick,翻译成时钟打点。跟它配套的还有一个常数,叫CLK_TCK,实际上就是clock tick的一个缩写,即这个机器时钟每秒钟所走的时钟打点的数。那这个数到底等于多少呢?不同的机器可能都不一样,我的电脑这个值为1000。
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <time.h>
clock_t start, stop;
/* clock_t是clock()函数返回的变量类型*/
double duration;
/* 记录被测函数运行时间,以秒为单位*/
int main()
{
/* 不在测试范围内的准备工作写在clock()调用之前*/
start = clock(); /* 开始计时*/
MyFunction(); /* 把被测函数加在这里*/
stop = clock(); /* 停止计时*/
duration = ((double)(stop - start)) / CLK_TCK; /* 计算运行时间*/
/* 其他不在测试范围的处理写在后面,例如输出duration的值*/
return 0;
}
下面我们就一个具体的多项式来看一下,这是一个9阶的多项式,它的第 i 个系数就等于 i 。然后我们要计算这个函数在1.1这个地方的函数值。我们为了区别起见,给这两个函数第一个取名叫做f1,第二个取名叫做f2。然后我们来跑一下,看看它们分别跑了多少时间。
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <time.h>
#include <math.h>
clock_t start, stop;
double duration;
#define MAXN 10 /* 多项式最大项数,即多项式阶数+1 */
double f1(int n, double a[], double x);
double f2(int n, double a[], double x);
int main()
{
int i;
double a[MAXN]; /* 存储多项式的系数*/
for (i = 0; i < MAXN; i++) a[i] = (double)i; //a[i] = i
start = clock();
f1(MAXN - 1, a, 1.1);
stop = clock();
duration = ((double)(stop - start)) / CLK_TCK;
printf("ticks1 = %f\n", (double)(stop - start));
printf("duration1 = %6.2e\n", duration);
start = clock();
f2(MAXN - 1, a, 1.1);
stop = clock();
duration = ((double)(stop - start)) / CLK_TCK;
printf("ticks2 = %f\n", (double)(stop - start));
printf("duration2 = %6.2e\n", duration);
return 0;
}
double f1(int n, double a[], double x)
{
int i;
double p = a[0];
for (i = 1; i <= n; i++)
p += (a[i] * pow(x, i));
return p;
}
double f2(int n, double a[], double x)
{
int i;
double p = a[n];
for (i = n; i > 0; i--)
p = a[i - 1] + x * p;
return p;
}
运行,可以看到时间全为0。这是因为这两个函数跑得实在是太快了,它们的运行时间都不到一个tick,所以这个clock函数根本就捕捉不到它的区别。

因此,我们让这两个函数重复地跑,直到这个间隔的时间能够被clock这个函数捕捉到。最后计算它单次时间的时候,你只要把总时间除以重复的次数就得到了这个函数一次运行的时间。因此,我们将函数稍微改一下。
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <time.h>
#include <math.h>
clock_t start, stop;
double duration;
#define MAXN 10 /* 多项式最大项数,即多项式阶数+1 */
#define MAXK 1e7 /* 被测函数最大重复调用次数*/
double f1(int n, double a[], double x);
double f2(int n, double a[], double x);
int main()
{
int i;
double a[MAXN]; /* 存储多项式的系数*/
for (i = 0; i < MAXN; i++) a[i] = (double)i; //a[i] = i
start = clock();
for (i = 0; i < MAXK; i++) /* 重复调用函数以获得充分多的时钟打点数*/
{
f1(MAXN - 1, a, 1.1);
}
stop = clock();
duration = ((double)(stop - start)) / CLK_TCK /MAXK; /* 计算函数单次运行的时间*/
printf("ticks1 = %f\n", (double)(stop - start));
printf("duration1 = %6.2e\n", duration);
start = clock();
for (i = 0; i < MAXK; i++)
{
f2(MAXN - 1, a, 1.1);
}
stop = clock();
duration = ((double)(stop - start)) / CLK_TCK /MAXK; /* 计算函数单次运行的时间*/
printf("ticks2 = %f\n", (double)(stop - start));
printf("duration2 = %6.2e\n", duration);
return 0;
}
double f1(int n, double a[], double x)
{
int i;
double p = a[0];
for (i = 1; i <= n; i++)
p += (a[i] * pow(x, i));
return p;
}
double f2(int n, double a[], double x)
{
int i;
double p = a[n];
for (i = n; i > 0; i--)
p = a[i - 1] + x * p;
return p;
}
来看看运行时间,结果如下。所以我们就可以看到,为什么说第一个算法比较傻呢,它比第二个算法要慢了差不多一个数量级的样子
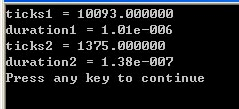
这个故事告诉我们:解决问题方法的效率,还跟算法的巧妙程度是有关系的
1.4 抽象数据类型
所以到底什么是数据结构?
• 数据结构是关于数据对象在计算机中的组织方式。我们在这儿介绍数据对象的组织方式的时候,其实是有两个概念在这里。一个是关于数据对象的逻辑结构,另外一个是数据对象在计算机里面的物理存储结构。
----• 逻辑结构
什么是逻辑结构呢?以前面存放图书为例,我们如果一开始把这个书架想象成简单的一长条,然后所有的书是一个挨着一个放的。如果每一本书有一个编号的话,那么这种结构是一对一的结构,我们管它叫做线性结构。
另外,我先把图书分类并给每一类一个编号。那么这一个类别的编号里边,对应着很多本书,这是一个一对多的逻辑结构,这种结构有个名字叫做树。
假设我们还统计这样的一些信息:这一本书都有哪些人买过,买了这本书的人还买过其它的什么书。于是呢,其实就是一本书对应着很多人,而一个人又对应了很多本书,这是一个多对多的、很复杂的一个关系网,那么这个关系网对应的就是一个图的结构。
----• 物理存储结构
我们说的这些逻辑结构在机器的内存里面到底要怎么一个放法。是连续着放呢?还是东一个西一个隔开放呢?也就是说,是用一个数组来存它呢?还是用一个链表来存它呢?这个就是属于物理存储结构。
• 数据对象必定与一系列加在其上的操作相关联
• 完成这些操作所用的方法就是算法
描述数据结构,我们有一个很好的方法,叫做抽象数据类型(Abstract Data Type)
在这里头我们有两个关键词一个叫“数据类型”,一个词是“抽象”,它们分别是什么意思呢?
• 数据类型
• 数据对象集
就是我们在说的“是什么东西”
• 数据集合相关联的操作集
就像我们说,我们不能单纯地讲怎么去处理图书,我们是要对这些图书去做操作的
• 抽象:描述数据类型的方法不依赖于具体实现
• 与存放数据的机器无关
• 与数据存储的物理结构无关
• 与实现操作的算法和编程语言均无关
只描述数据对象集和相关操作集“是什么”,并不涉及“如何做到”的问题。
例:“矩阵”的抽象数据类型定义
我们接下来看一个例子,可以帮助你更好地理解这个抽象数据类型到底是个什么东西。我们这个例子是关于一个“矩阵”的抽象数据类型的定义。
类型名称:首先我们要给这个抽象数据类型一个名称,叫做矩阵(Matrix)
数据对象集:然后我们要描述一下它的数据对象集。一个 M × N {\rm{M \times N}} M×N的矩阵 A M × N = ( a i j ) ( i = 1 , . . . , M ; j = 1 , . . . , N ) { {\rm{A}}_{ {\rm{M \times N}}}} = ({a_{ij}})(i = 1,...,M;j = 1,...,N) AM×N=(aij)(i=1,...,M;j=1,...,N),是由 M × N {\rm{M \times N}} M×N个三元组 < a , i , j > < a,i,j > <a,i,j>构成。其中a是矩阵元素的值,i是元素所在的行号,j是元素所在的列号。
操作集:相关联的操作集有很多,在这里头列了一些比较简单的。对于任意矩阵 A 、 B 、 C ∈ M a t r i x {\rm{A、B、C}} \in {\rm{Matrix}} A、B、C∈Matrix,以及整数 i 、 j 、 M 、 N {\rm{i、j、M、N}} i、j、M、N
----Matrix Create( int M, int N ):返回一个 M × N {\rm{M \times N}} M×N的空矩阵;
----int GetMaxRow( Matrix A ):返回矩阵A的总行数;
----int GetMaxCol( Matrix A ):返回矩阵A的总列数;
----ElementType GetEntry( Matrix A, int i, int j ):返回矩阵A的第i行、第j列的元素;
----Matrix Add( Matrix A, Matrix B ):如果A和B的行、列数一致,则返回矩阵C=A+B,否则返回错误标志;
----Matrix Multiply( Matrix A, Matrix B ):如果A的列数等于B的行数,则返回矩阵C=AB,否则返回错误标志;
二、什么是算法
2.1 算法的定义
算法的定义:
• 算法(Algorithm)的定义要比数据结构容易定义一点,它包含这么几个要素
• 算法是一个有限指令集
就是一堆指令放在一起,去做一件事情,而这个指令集一定是有限的
• 接受一些输入(有些情况下不需要输入)
• 产生输出
算法一定会产生至少一个输出,否则的话这个算法就没有什么意义了
• 一定在有限步骤之后终止
算法跟我们的程序不一样,有些程序可以一直跑,比如说操作系统,只要你不关机它就一直跑在上面。而算法是不能有这种无限循环的概念的。
• 每一条指令必须
• 有充分明确的目标,不可以有歧义
• 计算机能处理的范围之内
• 描述应不依赖于任何一种计算机语言以及具体的实现手段
我们来看下面一个例子,这个例子是关于选择排序算法的一个伪码描述。那么,选择排序算法是怎么一回事呢?我从还没有排好序的这堆元素中间,每次选一个最小的元素把它贴到已经排好序的那个子序列的最后面。于是重复这个过程,最后得到的就是一个从小到大排好序的序列。
void SelectionSort ( int List[], int N )
{
/* 将N个整数List[0]...List[N-1]进行非递减排序*/
for ( i = 0; i < N; i ++ ) {
MinPosition = ScanForMin( List, i, N–1 );
/* 从List[i]到List[N–1]中找最小元,并将其位置赋给MinPosition */
Swap( List[i], List[MinPosition] );
/* 将未排序部分的最小元换到有序部分的最后位置*/
}
}
上面这段伪码描述一个很重要的特点是:抽象。我们看上去好像它很具体的样子,其实它还是抽象的。抽象在哪里呢?
第一点,这个List,虽然我们写得好像把它写成了一个数组的样子。但是,它非要是个数组不可吗?不一定的。我如果传进来的是一个链表的话,整个的算法依然是正确的。
第二点,这个Swap,我们写上去好像是把它写成了一个函数的样子。但是我一定要用一个函数去实现swap(交换)吗?我是不是可以写一个宏去实现?这个都是具体实现的细节,在我们描述算法的时候是不关心的
2.2 什么是好的算法
解决同一个问题的时候,我们通常会有很多种不一样的算法。区别就在于,有的算法比较笨,有的算法比较聪明。那我们怎么去衡量它们谁好谁坏呢?我们通常有下面的两个指标:
• 空间复杂度S(n) —— 根据算法写成的程序在执行时占用存储单元的长度。这个长度往往与输入数据的规模有关。空间复杂度过高的算法可能导致使用的内存超限,造成程序非正常中断。
• 时间复杂度T(n) —— 根据算法写成的程序在执行时耗费时间的长度。这个长度往往也与输入数据的规模有关。时间复杂度过高的低效算法可能导致我们在有生之年都等不到运行结果
—
为什么要把它们写成是一个 n 的函数呢?因为这两个指标跟我们要处理的数据的规模是直接相关的。举个例子说,我如果让你打印十个整数,你那个程序可能瞬间就给出结果了。如果我让你打印十万个整数呢?你就要多等一会儿了。所以这个程序运行的时间,跟我要你处理的数据是十个还是十万个跟这件事情是相关的。这个“十”或者“十万”,就是我们要处理的数据的规模,我们把它叫做 n。它是一个变量的话,那么我们这个程序所用的时间和空间都跟这个 n 是有直接关系的。
接下来我们来看两个例子。第一个例子是我们在前面看过的,就是使用递归写出来的打印 N 个整数的那个程序。
void PrintN ( int N )
{
if ( N ){
PrintN( N – 1 );
printf(“%d\n”, N );
}
return;
}
我们说这个递归的程序在N=100000的时候在我的机器上它就非正常跳出了。到底发生了什么事情呢?我们这儿来仔细地看一下:
①假设在内存里面我们有一块空间是这个程序可以用的。我们开始调用这个PrintN(100000),这个时候程序判断了这个 N 不为零,于是它递归调用PrintN(99999)。
②调用PrintN(99999)之前,你的系统需要把当前的这个函数PrintN(100000)所有的现有的状态都存到系统内存的某一个地方。
③我们调用PrintN(99999)时,会发现先得调用PrintN(99998),于是PrintN(99999)所有的状态要被存一下。然后我们调用PrintN(99998),然后继续存,继续存……
④一直到最后什么时候可以返回了呢?到我们调用PrintN(0)的时候,可以返回。那么在调用PrintN(0)之前呢,我们必定调用了PrintN(1)。所以最后存在系统里面的一块内容,应该是PrintN(1)这个函数所有的当前的状态。
于是我们就发现:
这个程序在内存里面占用的空间的数量实际上是跟这个原始的 N 的大小成正比的。也就是说,空间复杂度做为一个 N 的函数的话,是一个常数乘以 N,随着 N 来做线性增长。当这个 N 非常非常大的时候,你的程序可以用的空间是有限的,它把它有限的空间用爆掉了,所以它就非正常退出了。
那我们再去回想一下,那个循环实现的程序它有没有这个问题呢?
在那个程序里面,它只用了临时变量和一个for循环。它没有涉及到任何程序调用的问题,所以不管那个 N 有多大,它占用的空间始终都是固定的,不会随着 N 的增长而增长,所以它永远是没问题的。
接下来的例子我们再回顾一下前面说“求多项式的值”。我们说有一个函数特别傻,有一个函数很聪明。那么具体为什么会这样呢?机器运算加减法的速度比乘除法的速度要快很多。分析一个函数运行效率的时候,我们基本上就是在数函数到底做了多少次乘除法,加减法可以忽略不计。那我们现在就来具体地数一下,这两个函数分别做了多少次乘法:
1、常规方法
double f( int n, double a[], double x )
{
int i;
double p = a[0];
for ( i=1; i<=n; i++ )
p += (a[i] * pow(x, i));
return p;
}
第一个函数看上去我们只看到了一个乘号,这一个乘号出现在一个for循环里面,这个for循环一共执行了n次。但是不要忘了这个pow函数,这个算的是 x 的 i 次方,要做(i-1)次乘法。然后再加上这一次跟前面的系数相乘,所以每一次循环里面执行的是 i 次乘法。于是乘法的总次数就是从 1 一直加到 n,最后就得到 ( 1 + 2 + . . . . . . + n ) = ( n 2 + n ) / 2 {\rm{(1 + 2 + }}......{\rm{ + n) = (}}{ {\rm{n}}^{\rm{2}}}{\rm{ + n)/2}} (1+2+......+n)=(n2+n)/2这么多次乘法。
2、使用乘法结合律
double f( int n, double a[], double x )
{
int i;
double p = a[n];
for ( i=n; i>0; i-- )
p = a[i-1] + x*p;
return p;
}
第二个程序简单多了,每一个循环里面就只有 1 次乘法,一共执行了 n 次循环,所以我们一共只做了 n 次乘法。
所以当我们用时间复杂度这个概念去描述它们的时候,我们会说:
第一个函数它的时间复杂度作为 n 的函数,是一个常数乘以 n 平方,加上另一个常数乘以 n。 T ( n ) = C 1 n 2 + C 2 n T({\rm{n}}) = {C_1}{ {\rm{n}}^{\rm{2}}} + {C_2}{\rm{n}} T(n)=C1n2+C2n
而对第二个函数来说,它的时间复杂度应该就是一个常数乘以 n。 T ( n ) = C ⋅ n T({\rm{n}}) = C \cdot {\rm{n}} T(n)=C⋅n
我们仔细来看一下,这两个函数的比较。虽然常数C1、C2和C到底是什么,这个其实每台机器上跑起来可能都不太一样。但是,不管这三个常数是什么,我们知道当 n 充分大的时候,那个 n 平方其实是远远超过了 n 的。这就意味着当 n 很大的时候,第二个程序一定会跑得比第一个程序快很多很多
一般来说我们在分析算法的效率的时候,通常关心的是下面两种复杂度:
一个是最坏情况的复杂度: T w o r s t ( n ) {T_{worst}}(n) Tworst(n)
另外一个是平均复杂度: T a v g ( n ) {T_{avg}}(n) Tavg(n)
T a v g ( n ) ≤ T w o r s t ( n ) {T_{avg}}(n) \le {T_{worst}}(n) Tavg(n)≤Tworst(n)
很显然地我们知道,平均复杂度肯定是比最坏情况复杂度要小。但是我们在分析的时候,比较喜欢分析的是这个最坏情况复杂度。因为分析这个平均复杂度会非常之难,我们拣容易的做,最关心的就是最坏情况复杂度。
2.3 复杂度的渐进表示
当我们在分析一个算法复杂度的时候,我们没有必要一步一步去数,说它把哪个操作做了多少次。其实我们关心的只是说,随着要处理的数据的规模的增大,它这个复杂度增长的性质会怎么样。比如说,当我们在比较前面两个算法的时候,我们只要知道:第一个算法它的时间复杂度当 n 很大的时候,基本上就是 n 2 {n^2} n2在起主要作用。第二个。算法当 n n n 很大的时候,是 n n n 在起主要作用。我们知道当 n 充分大的时候,第一个算法肯定是要比第二个算法要慢的。所以我们从来不对算法做非常精细的分析,我们只粗略地知道它的一个增长趋势就可以了。于是就有了我们复杂度的渐进表示法。
T ( n ) = O ( f ( n ) ) T(n) = O(f(n)) T(n)=O(f(n))表示存在常数 C > 0 , n 0 > 0 C{\rm{ }} > 0,{\rm{ }}{n_0} > 0 C>0,n0>0使得当 n ≥ n 0 n \ge {n_0} n≥n0时有 T ( n ) ≤ C ⋅ f ( n ) T(n) \le C \cdot f(n) T(n)≤C⋅f(n)。 O ( f ( n ) ) O(f(n)) O(f(n))就表示 f ( n ) f(n) f(n)是 T ( n ) T(n) T(n)的某种上界.
T ( n ) = Ω ( g ( n ) ) T(n) = \Omega (g(n)) T(n)=Ω(g(n))表示存在常数 C > 0 , n 0 > 0 C{\rm{ }} > 0,{\rm{ }}{n_0} > 0 C>0,n0>0使得当 n ≥ n 0 n \ge {n_0} n≥n0时有 T ( n ) ≥ C ⋅ g ( n ) T(n) \ge C \cdot g(n) T(n)≥C⋅g(n)。 Ω ( g ( n ) ) \Omega (g(n)) Ω(g(n))就表示 g ( n ) g(n) g(n)是 T ( n ) T(n) T(n)的某种下界.
T ( n ) = θ ( h ( n ) ) T(n) = \theta (h(n)) T(n)=θ(h(n))表示同时有 T ( n ) = O ( h ( n ) ) T(n) = O(h(n)) T(n)=O(h(n))和 T ( n ) = Ω ( h ( n ) ) T(n) = \Omega (h(n)) T(n)=Ω(h(n))。对于这个 θ \theta θ里面的函数来说, O O O和 Ω \Omega Ω是同时成立的,也就是说,它既是上界也是下界,它们基本上是等价的。
接下来看一些图表,增加一下对不同复杂度函数的感性理解。下面这张表给大家显示了不同的函数随着 n 的增长,它的增长的速度。
| 函数 | 1 | 2 | 4 | 8 | 16 | 32 |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| log n \log n logn | 0 | 1 | 2 | 3 | 4 | 5 |
| n n n | 1 | 2 | 4 | 8 | 16 | 32 |
| n log n n\log n nlogn | 0 | 2 | 8 | 24 | 64 | 160 |
| n 2 {n^2} n2 | 1 | 4 | 16 | 64 | 256 | 1024 |
| n 3 {n^3} n3 | 1 | 8 | 64 | 512 | 4096 | 32768 |
| 2 n {2^n} 2n | 2 | 4 | 16 | 256 | 65536 | 4294967296 |
| n ! n! n! | 1 | 2 | 24 | 40326 | 2092278988000 | 26313 × 1 0 33 26313 \times {10^{33}} 26313×1033 |
我们接着看下面这张图,它更直观地显示了各种不同的函数的增长速率。

下面这个表格给了一个具体的时间,让你体会得更深刻一点。我们假设我们有一个每秒钟执行10亿个指令的计算机,然后每一列对应了一个复杂度的函数。我们先看这个指数, n 2 {n^2} n2。当 n 只不过是100的时候,你的程序就不要想跑出结果了,世界末日你都等不到结果了。

复杂度分析小窍门
①若两段算法分别有复杂度 T 1 ( n ) = O ( f 1 ( n ) ) {T_1}(n) = O({f_1}(n)) T1(n)=O(f1(n))和 T 2 ( n ) = O ( f 2 ( n ) ) {T_2}(n) = O({f_2}(n)) T2(n)=O(f2(n)),则
---- T 1 ( n ) + T 2 ( n ) = max ( O ( f 1 ( n ) ) , O ( f 2 ( n ) ) ) {T_1}(n) + {T_2}(n) = \max (O({f_1}(n)),O({f_2}(n))) T1(n)+T2(n)=max(O(f1(n)),O(f2(n)))
---- T 1 ( n ) × T 2 ( n ) = O ( f 1 ( n ) × f 2 ( n ) ) {T_1}(n) \times {T_2}(n) = O({f_1}(n) \times {f_2}(n)) T1(n)×T2(n)=O(f1(n)×f2(n))
②若 T ( n ) T(n) T(n)是关于 n n n的 k k k阶多项式,那么 T ( n ) = θ ( n k ) T(n) = \theta ({n^k}) T(n)=θ(nk)
③一个for循环的时间复杂度等于循环次数乘以循环体代码的复杂度。
④if-else 结构的复杂度取决于if的条件判断复杂度和两个分枝部分的复杂度,总体复杂度取三者中最大。
小测验
1、下列函数中,哪个函数具有最快的增长速度:
A. N ( log N ) 2 N{(\log N)^2} N(logN)2
B. N 2 log N {N^2}\log N N2logN
C. N 3 {N^3} N3
D. N log ( N 2 ) N\log ({N^2}) Nlog(N2)
答案:C
2、下面一段代码的时间复杂度是?
if ( A > B ) {
for ( i=0; i<N; i++ )
for ( j=N*N; j>i; j-- )
A += B;
}
else {
for ( i=0; i<N*2; i++ )
for ( j=N*2; j>i; j-- )
A += B;
}
A. O ( N ) O(N) O(N)
B. O ( N 2 ) O({N^2}) O(N2)
C. O ( N 3 ) O({N^3}) O(N3)
D. O ( N 4 ) O({N^4}) O(N4)
答案:C
三、应用实例:最大子列和问题
3.1 算法1与算法2:暴力搜索
所谓最大子列和问题就是给定 N 个整数的序列 { A 1 , A 2 , . . . , A N } \{ {A_1},{A_2},...,{A_N}\} {
A1,A2,...,AN},我们要求函数 f ( i , j ) = max { 0 , ∑ k = i j A k } f(i,j) = \max \{ 0,\sum\limits_{k = i}^j {
{A_k}} \} f(i,j)=max{
0,k=i∑jAk}的最大值。这是一个什么函数呢?就是从 A i {A_i} Ai到 A j {A_j} Aj连续的一段子列的和。对 N 个整数来说,有很多这样的连续的子列,我们要求的是所有连续子列和里面最大的那个。如果这个和是负数的话,我们最后就返回 0 做为结束。
算法1:要解决这个问题呢,其实有好多好多不同的算法。一个最直接、最暴力的办法就是:我把所有的连续子列和全部都算出来,然后从中找最大的那一个。总的来说我们是有 2 重循环,最外面这层循环 i i i 对的是子列左端的位置,是从 A [ i ] A[i] A[i] 开始。然后 j j j 对的是子列和的右边的位置,一直到 A [ j ] A[j] A[j] 为止。所以 j j j 总是大于等于 i i i 的,从 i i i 开始计数。在这个双重循环里面,我们就开始暴力地去求这个子列和。所以我们还需要一重循环叫做 k k k, k k k 从 i i i 一直加到 j j j。变量ThisSum就是当前的这个和,从 A [ i ] A[i] A[i] 一直加到 A [ j ] A[j] A[j]。加完了以后看一下,这个和如果要大的话,那我们更新一下这个最大和。现在考虑一下,这个算法复杂度是多少呢?我们的答案是: O ( N 3 ) O(N^3) O(N3)
int MaxSubseqSum1(int A[], int N)
{
int ThisSum, MaxSum = 0;
int i, j, k;
for (i = 0; i < N; i++) {
/* i是子列左端位置*/
for (j = i; j < N; j++) {
/* j是子列右端位置*/
ThisSum = 0; /* ThisSum是从A[i]到A[j]的子列和*/
for (k = i; k <= j; k++)
ThisSum += A[k];
if (ThisSum > MaxSum) /* 如果刚得到的这个子列和更大*/
MaxSum = ThisSum; /* 则更新结果*/
} /* j循环结束*/
} /* i循环结束*/
return MaxSum;
}
算法2:我们看到有一个很大的问题就是说当我们知道当前从 i 到 j 的和的时候,我们要计算下一个 j 的时候,没有必要从头开始往后加。所以当 j 增加了 1 的时候,我们其实只要在前面那个 i 到 j 的部分和后面加1个元素就好了,我没有必要要那个k循环的,这个k循环完全是多余的,这样就有了我们的算法2。我们在外面仍然有一个 i 循环,i 是子列的左端位置。仍然我们有这个 j 循环,j 是子列右端的位置。不同的是ThisSum,j 每增加一个值的时候只是在当前这个部分和的基础上,加一个 A [ j ] A[j] A[j] 就可以了。这个算法的复杂度是多少呢?很显然,我们是有两重循环的嵌套,所以答案应该是 O ( N 2 ) O(N^2) O(N2)
int MaxSubseqSum2( int A[], int N )
{
int ThisSum, MaxSum = 0;
int i, j;
for( i = 0; i < N; i++ ) {
/* i是子列左端位置*/
ThisSum = 0; /* ThisSum是从A[i]到A[j]的子列和*/
for( j = i; j < N; j++ ) {
/* j是子列右端位置*/
ThisSum += A[j];
/*对于相同的i,不同的j,只要在j-1次循环的基础上累加1项即可*/
if( ThisSum > MaxSum ) /* 如果刚得到的这个子列和更大*/
MaxSum = ThisSum; /* 则更新结果*/
} /* j循环结束*/
} /* i循环结束*/
return MaxSum;
}
3.2 算法3:分而治之
我们的第三个算法有一个很高大上的名字,叫做分而治之。分而治之的思想可以用来解决很多的问题,大概的思路就是把一个比较大的复杂的问题切分成小的块,然后分头去解决它们,最后再把结果合并起来。
针对最大子列和问题,我们先把这个数组从中间一分为二,然后递归地去解决左右两边的问题。递归地去解决左边的问题,我们会得到左边的一个最大子列和。递归地去解决右边的问题,我们得到右边的一个最大子列和。然后我们可以说这两个数中间最大的一个就一定是结论吗?那可不一定。还有一种情况就是跨越边界的最大子列和。把这三个结果找到了以后,那我们真的可以说我们最后的结果一定是这三个数中间最大的那一个。

为了能更好地理解这个算法,我们来看一个具体的例子。比如说我们给了以下 8 个数字,并求其最大子序列之和。
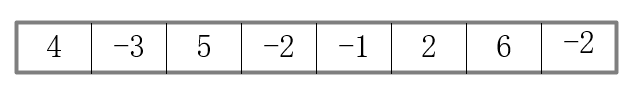
第一步我们先从中间把它一分为二,然后递归地先解决左半边。在递归地进入左半边的时候,我们继续把它一分为二,继续地递归到左半边,然后继续分…….对于最左边的最小的子列,返回最大值为4。

同理,可以求出左边序列的最大子序列和为6.

类似的,我们由底向上分析右边的子列,可以得到右边子列最大子序列和为8。

最后,分析两边子列和跨越边界的子列,可以得到最大子列和为11。

你现在能不能先猜一猜它的复杂度会是多少呢?分析这种递归的算法,略微有一点难度。
1、当我解决的整个问题里有 N N N 个数字的时候,如果复杂度记做 T ( N ) T(N) T(N) 的话,那么我得到这半边数字的时间复杂度就应该是 T ( N / 2 ) T(N/2) T(N/2),因为我的规模减半了。同样的道理,我得到这一半递归结果的时间复杂度也应该是 T ( N / 2 ) T(N/2) T(N/2)。
2、而我是怎么得到中间这个跨边界最大子列和的呢?我们的做法就是,从中间开始,往左边扫描,然后往右边扫描,每一个元素都被扫描了一次。所以,得到这个结果的复杂度应该是 N N N 的一个常数倍。由此我们就得到了关于 T ( N ) T(N) T(N) 的一个递推公式 T ( N ) = 2 T ( N / 2 ) + c N T(N) = 2T(N/2) + cN T(N)=2T(N/2)+cN。也就是说, T ( N ) T(N) T(N) 是由“算出左边“的复杂度加上”算出右边“的复杂度加上“跨越中间”的复杂度这三部分组成的,也就是两倍的 T ( N / 2 ) T(N/2) T(N/2) 加上一个 N N N 的常数倍。
3、然后我们递推 k k k次,最后结果下:
T ( N ) = 2 T ( N / 2 ) + c N = 2 [ 2 T ( N / 2 2 ) + c N / 2 ] + c N = 2 k O ( 1 ) + c k N = O ( N log N ) 其 中 , N / 2 k = 1 \begin{array}{l} T(N) = 2T(N/2) + cN\\ = 2[2T(N/{2^2}) + cN/2] + cN\\ = {2^k}O(1) + ckN\\ = O(N\log N)\\ 其中,N/{2^k} = 1 \end{array} T(N)=2T(N/2)+cN=2[2T(N/22)+cN/2]+cN=2kO(1)+ckN=O(NlogN)其中,N/2k=1
3.3 算法4:在线处理
我们前边说, N l o g N NlogN NlogN 已经是很快的算法了。但是就解决这个问题来说,它仍然不是最快的。我们还有一个更快的算法,叫做在线处理算法。这个算法描述里面只有一个 for 循环,for循环里面所有的if-else这些东西都是常数数量级的复杂度。所以很显然,这个算法的复杂度就是 O ( N ) O(N) O(N),是线性的。这个必须是我们可能得到的最快的一个算法了,因为无论如何我们总得把每一个元素看一遍吧,就我读输入也需要 O ( N ) O(N) O(N) 的时间。
int MaxSubseqSum4( int A[], int N )
{
int ThisSum, MaxSum;
int i;
ThisSum = MaxSum = 0;
for( i = 0; i < N; i++ ) {
ThisSum += A[i]; /* 向右累加*/
if( ThisSum > MaxSum )
MaxSum = ThisSum; /* 发现更大和则更新当前结果*/
else if( ThisSum < 0 ) /* 如果当前子列和为负*/
ThisSum = 0; /* 则不可能使后面的部分和增大,抛弃之*/
}
return MaxSum;
}
算法的运行过程如下:

为什么这个算法叫“在线处理”呢?我们看到整个的处理过程是什么样的呢?就是一个数字一个数字地读进来,我的输入
如果读入4后突然停住,后面的输入不读了,那么现在这个程序就应该给我返回 5 作为当前的最大子列和。而这个结果是对的,对于前 4 个数字而言,的确返回了5这个正确结果。这个就叫做“在线处理”。
接下来这张表是在某一台机器上跑出来的结果。 N 3 N^3 N3的这个算法跑到 N 等于1万的时候就已经跑不动了。(NA 的意思是 Not Available,就是不算了)。 N 2 N^2 N2算到10万的时候,它也算不下去了。而我们看 N l o g N NlogN NlogN,最后虽然也多花了几秒钟,但仍然是可以在几秒钟内给出结果的。而表现最好的当然是线性的算法,N 等于10万的时候,仍然是在小于 1 秒的时间内给出结果。

