做深度学习时常用到随机梯度下降方法,但是这个方法并不是在任何情况下都是有效的,也存在一些坑,可能是随机梯度下降失效导致模型效果不好。
1 随机梯度下降为什么会失效?
先介绍下梯度下降算法
经典的梯度下降方法的梯度:
▽ L ( θ ) = 1 M ∑ i = 1 M ▽ L ( f ( x i , θ ) , y i ) \triangledown L(\theta) = \frac{1}{M}\sum_{i=1}^{M} \triangledown L(f(x_i, \theta), y_i) ▽L(θ)=M1i=1∑M▽L(f(xi,θ),yi)
小批量梯度下降(m << M):
▽ L ( θ ) = 1 m ∑ i = 1 m ▽ L ( f ( x i , θ ) , y i ) \triangledown L(\theta) = \frac{1}{m}\sum_{i=1}^{m} \triangledown L(f(x_i, \theta), y_i) ▽L(θ)=m1i=1∑m▽L(f(xi,θ),yi)
随机梯度下降方法的梯度:
▽ L ( θ ) = ▽ L ( f ( x i , θ ) , y i ) \triangledown L(\theta) = \triangledown L(f(x_i, \theta), y_i) ▽L(θ)=▽L(f(xi,θ),yi)
梯度更新公式:
θ t + 1 = θ t − α g t , 其 中 g t = ▽ L ( θ t ) , − g t 表 示 步 子 方 向 \theta_{t+1} = \theta_t - \alpha g_t , 其中 g_t = \triangledown L(\theta_t), -g_t表示步子方向 θt+1=θt−αgt,其中gt=▽L(θt),−gt表示步子方向
由公式可以看出,为了准确的梯度,经典的梯度下降每次加载整个数据集计算梯度,需要花费大量的时间和内存,无法应用到大数据集场景;而随机梯度下降为了降低内存和时间开销,放弃了对准确度的追求,每次计算梯度只用一个样本,由于一个样本信息有限,对梯度的估计会有偏差,导致收敛不稳定或者不收敛。单个样本更新参数大大加快了收敛速度,适用于源源不断的在线更新,但是容易陷入到局部最优解中。因此为了折衷这两种方法,使迭代更加稳定,同时充分利用高度优化的矩阵计算,实际应用中会采用小批量梯度下降。
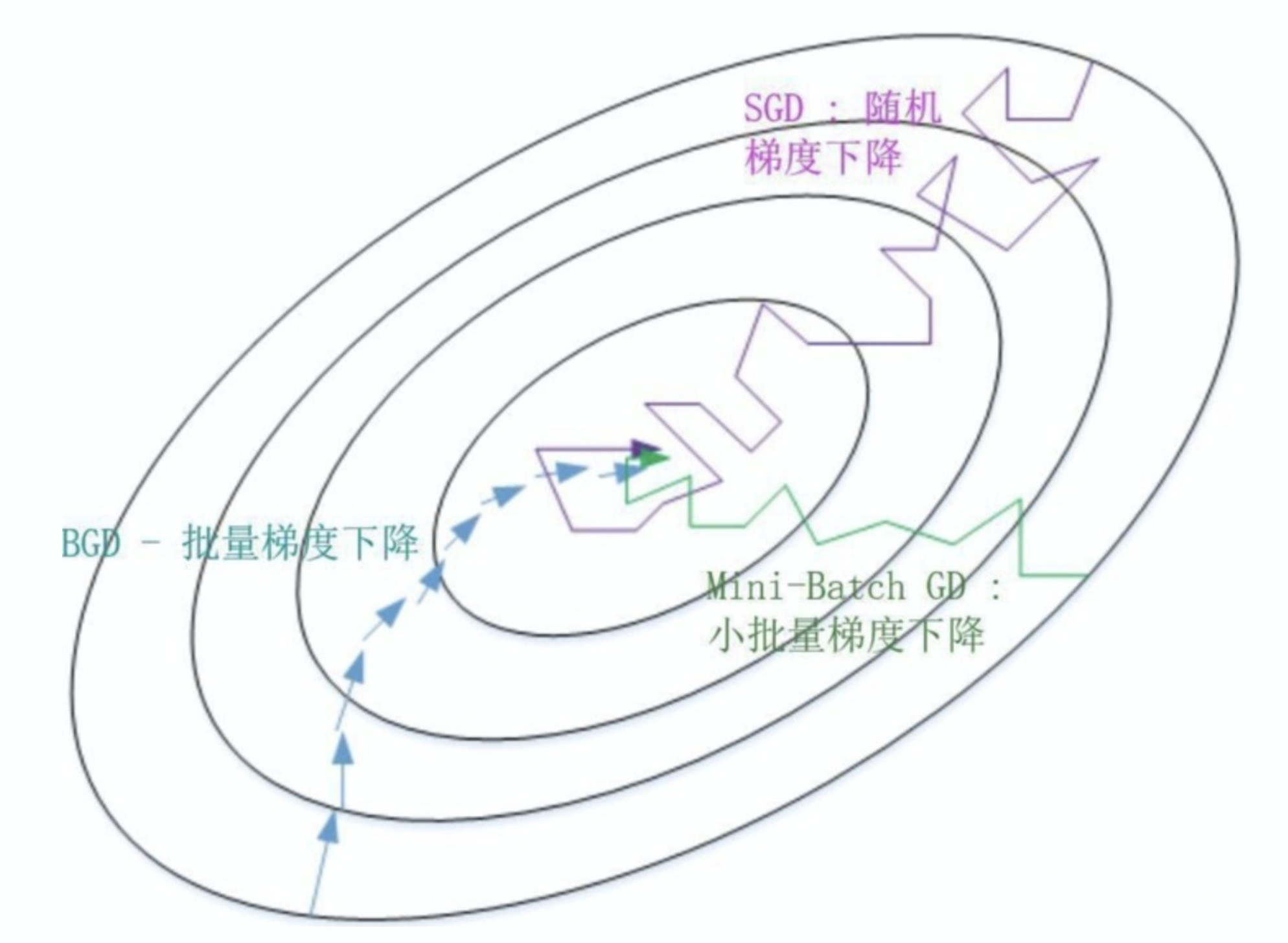
随机梯度下降最怕遇见山谷和鞍点两种地形。在山谷中,准确的梯度方向是沿山道向下,稍有偏差就会撞向山壁,而粗糙的梯度估计使得它在两山壁之间来回反弹振荡,不能沿山道方向迅速下降,导致收敛不稳定和收敛速度慢。在鞍点处,随机梯度下降法会走入一片平坦之地(此时离最低点还很远)。想象蒙着眼睛只凭借脚底感觉坡度,如果坡度很明显,那么基本能估计出下山的大致方向;如果坡度不明显,则很可能走错方向。同样,在梯度近乎为零的区域,随机梯度下降无法准确察觉出梯度的微小变化,结果就停滞下来。
注:鞍点指目标函数在此点上的梯度(一阶导数)值为 0, 但从改点出发的一个方向是函数的极大值点,而在另一个方向是函数的极小值点。
2 常用的解决方法有哪些?
2.1 添加动量
动量梯度下降法就是在梯度下降法中,迭代点的更新方向由当前的负梯度方向和上一次的迭代更新方向加权组合形成。一方面是加快下降,因为在下降的方向上不断累积动量,使得下降的速度变快了。另一方面,这样的方式可以使迭代跳出鞍点和部分较浅的局部极小值点,使更有可能找到全局极小值。
v t = γ v t − 1 + α g t v_t = \gamma v_{t-1} + \alpha g_t vt=γvt−1+αgt
θ t + 1 = θ t − v t \theta_{t+1} = \theta_t - v_t θt+1=θt−vt
− v t -v_t −vt表示步子前进方向,包含两部分,一个是学习旅乘以当前估计的梯度,另一个是带衰减的前一次步伐(惯性)
与随机梯度下降相比,动量方法收敛更快。
2.2 adagrad
动量方法是基于历史信息的,adagrad是机遇周围环境的感知。对环境的感知是指在参数空间中,根据不同参数的一些经验性判断,自适应的确定参数的学习速率,不同参数的更新速率不同(更新频率低的参数有更大的更新步子,更新频率高的有更小的步子)。该方法采用历史梯度平方和不同参数的梯度的稀疏性,越小越稀疏。
θ t + 1 , i = θ t , i − α g t , i ∑ k = 0 t g k , i 2 + ϵ \theta_{t+1,i} = \theta_{t,i} -\alpha \frac{g_{t,i}}{\sqrt{\sum_{k=0}^{t}g_{k,i}^2+\epsilon}} θt+1,i=θt,i−α∑k=0tgk,i2+ϵgt,i
θ t + 1 , i \theta_{t+1,i} θt+1,i表示 t + 1 t+1 t+1时刻的参数向量 θ t + 1 \theta_{t+1} θt+1的第 i i i个参数, g k , i g_{k,i} gk,i表示 k k k时刻的梯度向量 g k g_k gk的第 i i i个维度。分母有着退火的思想,随之时间推移, g t , i ∑ k = 0 t g k , i 2 + ϵ \frac{g_{t,i}}{\sqrt{\sum_{k=0}^{t}g_{k,i}^2+\epsilon}} ∑k=0tgk,i2+ϵgt,i越来越小,保证算法最终收敛。
2.3 adam
adam考虑了动量和环境感知。一方面,记录梯度的一阶矩(过往梯度与当前梯度的平均),体现了惯性(动量)思想,另一方面,记录梯度的二阶矩,即过往梯度平方与当前梯度平方的平均,体现了环境感知能力。
m t = β 1 m t − 1 + ( 1 − β 1 ) g t m_t = \beta_1 m_{t-1} + (1-\beta_1) g_t mt=β1mt−1+(1−β1)gt
v t = β 2 v t − 1 + ( 1 − β 2 ) g t 2 v_t = \beta_2 v_{t-1} + (1-\beta_2) g_t^2 vt=β2vt−1+(1−β2)gt2
θ t + 1 , i = θ t , i − α m ^ t v ^ t + ϵ \theta_{t+1,i} = \theta_{t,i} -\alpha \frac{\hat{m}_t}{\sqrt{\hat{v}_t}+\epsilon} θt+1,i=θt,i−αv^t+ϵm^t
其中, m ^ t = m t 1 − β 1 t \hat{m}_t = \frac{m_t}{1-\beta_1^t} m^t=1−β1tmt, v ^ t = v t 1 − β 2 t \hat{v}_t = \frac{v_t}{1-\beta_2^t} v^t=1−β2tvt
欢迎关注微信公众号(算法工程师面试那些事儿),本公众号聚焦于算法工程师面试,期待和大家一起刷leecode,刷机器学习、深度学习面试题等,共勉~
