51NOD 1076 2条不相交的路径

描述

题解

边双连通问题，使用Tarjan算法可以KO.。

Tarjan算法:

来自百度百科:

算法介绍

如果两个顶点可以相互通达，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。

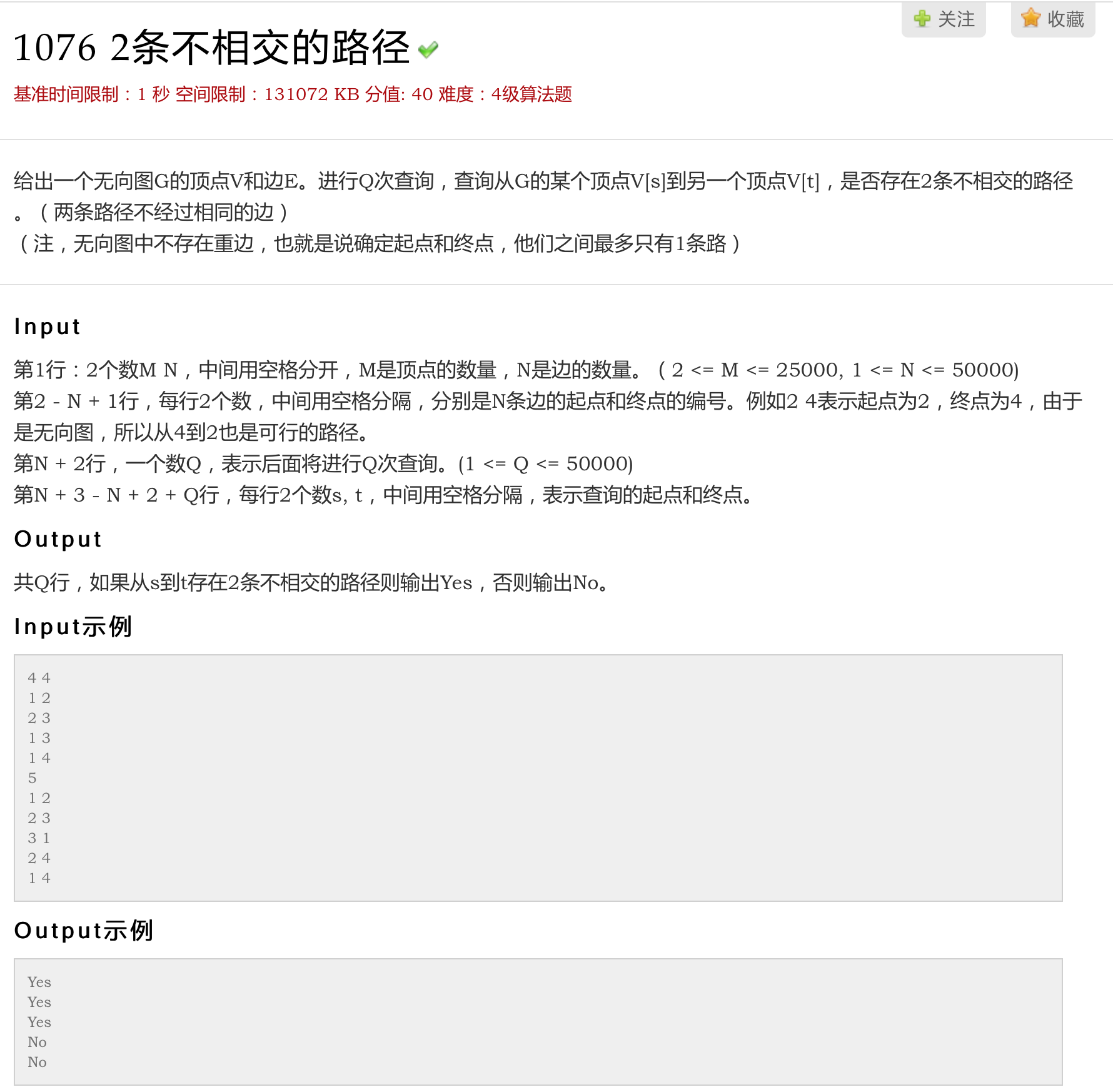
下图中，子图{1,2,3,4}为一个强连通分量，因为顶点1,2,3,4两两可达。{5},{6}也分别是两个强连通分量。

Tarjan算法是用来求有向图的强连通分量的。求有向图的强连通分量的Tarjan算法是以其发明者Robert Tarjan命名的。Robert Tarjan还发明了求双连通分量的Tarjan算法。

Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。

定义 DFN(u)为节点u搜索的次序编号( 时间戳)，Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号。

当DFN(u)=Low(u)时，以u为根的搜索子树上所有节点是一个强连通分量。

接下来是对算法流程的演示。

从节点1开始DFS，把遍历到的节点加入栈中。搜索到节点u=6时， DFN[6]=LOW[6]，找到了一个强连通分量。退栈到u=v为止，{6}为一个强连通分量。

返回节点5，发现DFN[5]=LOW[5]，退栈后{5}为一个强连通分量。

返回节点3，继续搜索到节点4，把4加入堆栈。发现节点4向节点1有后向边，节点1还在栈中，所以LOW[4]=1。节点6已经出栈，(4,6)是横叉边，返回3，(3,4)为树枝边，所以LOW[3]=LOW[4]=1。

继续回到节点1，最后访问节点2。访问边(2,4)，4还在栈中，所以LOW[2]=DFN[4]=5。返回1后，发现DFN[1]=LOW[1]，把栈中节点全部取出，组成一个连通分量{1,3,4,2}。

至此，算法结束。经过该算法，求出了图中全部的三个强连通分量{1,3,4,2},{5},{6}。

可以发现，运行Tarjan算法的过程中，每个顶点都被访问了一次，且只进出了一次堆栈，每条边也只被访问了一次，所以该算法的时间复杂度为O(N+M)。

代码

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <vector>
#include <cstring>

using namespace std;

const int MAXN = 5e4 + 10;

int stack[MAXN];    //  每遍历一个点便入栈
int top;
bool inStack[MAXN]; //  判断某个点是否已经在栈里面

//  这两个数组至关重要
//  dfn[u]为节点u搜索的次序编号（时间戳）
//  low[u]为u或者u的子树能够追溯到的最早的栈中节点的次序号
int dfn[MAXN];
int low[MAXN];

int beLong[MAXN];   //  判断哪些点联通
int Bcnt, Dindex;   //  记录强连通个数和当前时间
vector<int> v[MAXN];    //  邻接表保存边
int N, M, Q;

void init()
{
    Bcnt = Dindex = top = 0;
    memset(dfn, -1, sizeof(dfn));
    memset(inStack, false, sizeof(inStack));
    for (int i = 0; i < MAXN; i++)
    {
        v[i].clear();
    }
    return ;
}

void tarjan(int u, int fa)
{
    dfn[u] = low[u] = ++Dindex;
    stack[++top] = u;
    inStack[u] = true;  //  入队列，置为true

    int u_size = (int)v[u].size();
    for (int i = 0; i < u_size; i++)
    {
        int k = v[u][i];

        if (dfn[k] == -1)               //  没有被访问过
        {
            tarjan(k, u);
            low[u] = min(low[u], low[k]);
        }
        else if (inStack[k] && k != fa) //  被访问过
        {
            low[u] = min(low[u], dfn[k]);
        }
    }
    if (dfn[u] == low[u])
    {
        Bcnt++;
        int tmp;
        do
        {
            tmp = stack[top--];
            beLong[tmp] = Bcnt;
            inStack[tmp] = false;   //  出队列，置为false
        } while (tmp != u);
    }
    return ;
}

void solve()
{
    for (int i = 1; i <= N; i++)
    {
        if (dfn[i] == -1)   //  没有搜索过则搜索
        {
            tarjan(i, -1);
        }
    }
}

int main(int argc, const char * argv[])
{
    init();

    cin >> N >> M;

    int a, b;
    for (int i = 0; i < M; i++)
    {
        scanf("%d %d", &a, &b);
        v[a].push_back(b);
        v[b].push_back(a);
    }

    solve();

    cin >> Q;
    while (Q--)
    {
        scanf("%d %d", &a, &b);
        if (beLong[a] == beLong[b])
        {
            printf("Yes\n");
        }
        else
        {
            printf("No\n");
        }
    }

    return 0;
}

51NOD 1076 2条不相交的路径

描述

题解

算法介绍

代码

猜你喜欢