二阶条件
等式约束
首先考虑只有等式约束的情况
min x ∈ R n f ( x ) s . t . c i ( x ) = 0 , i = 1 , 2 , ⋯ , m \begin{aligned} \min_{x\in\mathbb{R}^n} ~~& f(x) \\ \mathrm{s.t.} ~~& c_i(x) = 0,i = 1,2,\cdots,m \end{aligned} x∈Rnmin s.t. f(x)ci(x)=0,i=1,2,⋯,m
设最优解 x ∗ x^* x∗ 存在,且在点 x ∗ x^* x∗ 处向量 a i ∗ ( i ∈ E ) a_i^* ~(i \in\mathcal{E}) ai∗ (i∈E) 线性无关(即 LICQ 约束规范成立)。对于序列可行方向 p ∈ F ∗ p \in \mathcal{F}^* p∈F∗,存在可行序列 x ( k ) x^{(k)} x(k) 及对应的方向序列 p ( k ) → p p^{(k)} \to p p(k)→p。由可行性,有
f ( x ( k ) ) = f ( x ∗ + δ k p ( k ) ) = L ( x ∗ + δ k p ( k ) , λ ∗ ) f(x^{(k)}) = f(x^* + \delta_k p^{(k)}) = \mathcal{L}(x^* + \delta_k p^{(k)}, \lambda^*) f(x(k))=f(x∗+δkp(k))=L(x∗+δkp(k),λ∗)
因为 x ∗ x^* x∗ 是 L \mathcal{L} L 的稳定点( ∇ L = 0 \nabla \mathcal{L} = 0 ∇L=0),所以 L \mathcal{L} L 在 x ∗ x^* x∗ 处的二阶 Taylor 展式为
f ( x ∗ + δ k p ( k ) ) = L ( x ∗ + δ k p ( k ) , λ ∗ ) = f ∗ + 1 2 δ k 2 p ( k ) T W ∗ p ( k ) + o ( δ k ) \begin{aligned} f(x^* + \delta_k p^{(k)}) &= \mathcal{L}(x^* + \delta_k p^{(k)}, \lambda^*)\\ &=f^* + \frac{1}{2} \delta_k^2 {p^{(k)}}^T W^* p^{(k)} + o(\delta_k) \end{aligned} f(x∗+δkp(k))=L(x∗+δkp(k),λ∗)=f∗+21δk2p(k)TW∗p(k)+o(δk)
其中
W ∗ = ∇ x 2 L ( x ∗ , λ ∗ ) = ∇ 2 f ( x ∗ ) + ∑ i = 1 m λ i ∗ ∇ 2 c i ( x ∗ ) W^* = \nabla_x^2 \mathcal{L}(x^*,\lambda^*) = \nabla^2f(x^*) + \sum_{i=1}^m \lambda_i^*\nabla^2c_i(x^*) W∗=∇x2L(x∗,λ∗)=∇2f(x∗)+i=1∑mλi∗∇2ci(x∗)
表示 Lagrange 函数关于 x x x 的 Hessian 矩阵。
于是,有
f ( x ∗ + δ k p ( k ) ) δ k 2 = f ∗ δ k 2 + 1 2 p ( k ) T W ∗ p ( k ) + o ( δ k ) δ k 2 \frac{f(x^* + \delta_k p^{(k)})}{\delta_k^2} =\frac{f^*}{\delta_k^2} + \frac{1}{2} {p^{(k)}}^T W^* p^{(k)} + \frac{o(\delta_k)}{\delta_k^2} δk2f(x∗+δkp(k))=δk2f∗+21p(k)TW∗p(k)+δk2o(δk)
又 k → ∞ k \to \infty k→∞,且 x ∗ x^* x∗ 为局部极小点,可得
p ( k ) T W ∗ p ( k ) ≥ 0 {p^{(k)}}^T W^* p^{(k)}\geq 0 p(k)TW∗p(k)≥0
定理(二阶必要条件) 设 x ∗ x^* x∗ 为问题的局部极小点,且满足 KKT 条件,设对应的 Lagrange 乘子为 λ ∗ \lambda^* λ∗,则对任一序列可行反向 p p p,必有
p T W ∗ p ≥ 0 p^T W^* p \geq 0 pTW∗p≥0
推论 设 x ∗ x^* x∗ 为问题的局部极小点,且满足 KKT 条件,设对应的 Lagrange 乘子为 λ ∗ \lambda^* λ∗,若 F ∗ = F ∗ \mathcal{F}^* = F^* F∗=F∗,必有
p T W ∗ p ≥ 0 , ∀ p ∈ F ∗ p^T W^* p \geq 0, \forall p \in F^* pTW∗p≥0,∀p∈F∗
定理(二阶充分条件) 设 x ∗ x^* x∗ 是问题的 KKT 点,对应的 Lagrange 乘子为 λ ∗ \lambda^* λ∗,若条件
p T W ∗ p > 0 , ∀ p ∈ F ∗ p^TW^*p > 0, \forall p \in F^* pTW∗p>0,∀p∈F∗
成立,则 x ∗ x^* x∗ 是问题的严格局部极小点。
例 考虑问题
min f ( x ) = 1 2 ( x 1 − 1 ) 2 + 1 2 x 2 2 s . t . c ( x ) = x 1 − β x 2 2 = 0 \begin{aligned} \min~~& f(x) = \frac{1}{2}(x_1 - 1)^2 + \frac{1}{2}x_2^2 \\ \mathrm{s.t.}~~&c(x) = x_1 - \beta x_2^2 = 0 \end{aligned} min s.t. f(x)=21(x1−1)2+21x22c(x)=x1−βx22=0
讨论参数 β \beta β 取何值时, x ∗ = ( 0 , 0 ) T x^*=(0,0)^T x∗=(0,0)T 是局部极小点?
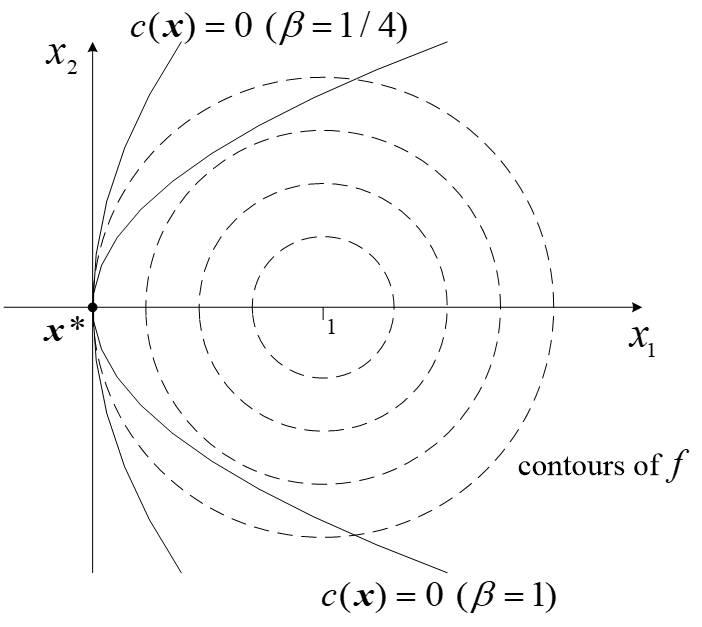
解 因为 g ∗ = ( − 1 , 0 ) T g^* = (-1,0)^T g∗=(−1,0)T, a ∗ = ( 1 , 0 ) T a^* = (1,0)^T a∗=(1,0)T,所以一阶条件满足, x ∗ x^* x∗ 是 KKT 点,且 λ ∗ = 1 \lambda^* = 1 λ∗=1, W ∗ = ( 1 0 0 1 − 2 β ) T W^* = \begin{pmatrix} 1 & 0 \\ 0 &1- 2\beta \end{pmatrix}^T W∗=(1001−2β)T
又 F ∗ = { p = ( 0 , p 2 ) T : p 2 ≠ 0 } F^* = \{p=(0,p_2)^T:p_2\neq0\} F∗={ p=(0,p2)T:p2=0},因此 p T W ∗ p = ( 1 − 2 β ) p 2 2 p^TW^*p = (1-2\beta)p_2^2 pTW∗p=(1−2β)p22。从而,有
- 当 β < 1 2 \beta < \frac{1}{2} β<21, x ∗ x^* x∗ 是严格局部极小点
- 当 β > 1 2 \beta > \frac{1}{2} β>21, x ∗ x^* x∗ 不是局部极小点
- 当 β = 1 2 \beta = \frac{1}{2} β=21, x ∗ x^* x∗ 是严格局部极小点
弱积极约束与强积极约束
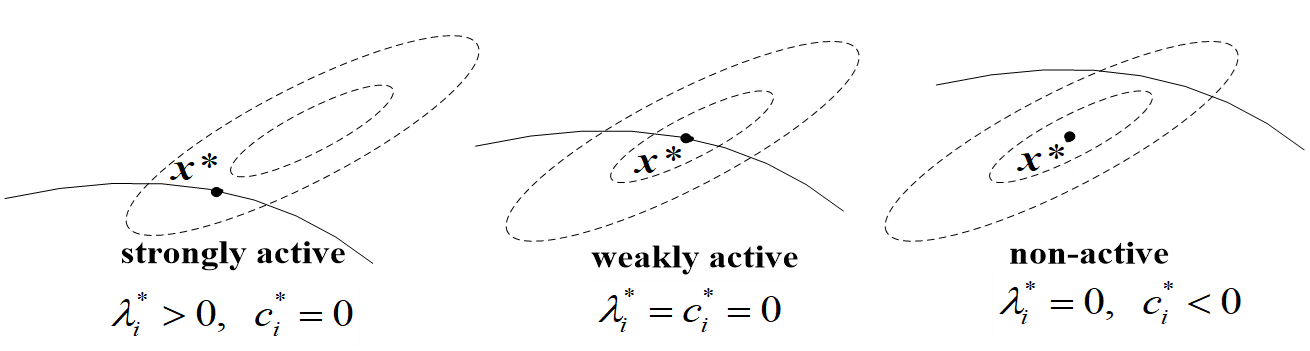
设 x ∗ x^* x∗ 是 KKT 点, λ ∗ \lambda^* λ∗ 是对应的 Lagrange 乘子。
定义
KaTeX parse error: Undefined control sequence: \or at position 41: …in\mathcal{E} ~\̲o̲r̲~ \lambda_i^* >…
为强积极约束集合。也就是从 A ∗ \mathcal{A}^* A∗ 中剔除弱积极约束,即 λ i ∗ = 0 , i ∈ I ∗ \lambda^*_i = 0,i\in\mathcal{I}^* λi∗=0,i∈I∗,得到 A + ∗ \mathcal{A}^*_+ A+∗。定义
G ∗ = { p ∈ F ∗ : c i ( x ( k ) ) = 0 , ∀ i ∈ A + ∗ } \mathcal{G}^* = \{p\in\mathcal{F}^*:c_i(x^{(k)}) = 0,\forall i \in \mathcal{A}^*_+\} G∗={ p∈F∗:ci(x(k))=0,∀i∈A+∗}G ∗ = { p ∈ R n : p ≠ 0 , a i ∗ T p = 0 , i ∈ A + ∗ , a i ∗ T p ≤ 0 , i ∈ A ∗ \ A + ∗ } G^* = \{p\in \mathbb{R}^n: p \neq 0, {a_i^*}^Tp = 0, i \in \mathcal{A}^*_+, {a_i^*}^Tp \leq 0, i \in \mathcal{A}^* \backslash \mathcal{A}_+^*\} G∗={ p∈Rn:p=0,ai∗Tp=0,i∈A+∗,ai∗Tp≤0,i∈A∗\A+∗}
事实上,有
- G ∗ ⊂ G ∗ \mathcal{G}^* \subset G^* G∗⊂G∗
- 设 p ∈ F ∗ p \in F^* p∈F∗,则 p T g ∗ = 0 p^T g^* = 0 pTg∗=0 当且仅当 p ∈ G ∗ p \in G^* p∈G∗
正则性假设 2 : G ∗ = G ∗ \mathcal{G}^* = G^* G∗=G∗
一般问题
首先一般约束优化问题
min x ∈ R n f ( x ) s . t . c i ( x ) = 0 , i ∈ E c i ( x ) ≤ 0 , i ∈ I \begin{aligned} \min_{x\in\mathbb{R}^n} ~~& f(x) \\ \mathrm{s.t.} ~~& c_i(x) = 0,i \in \mathcal{E}\\ & c_i(x) \leq 0,i \in \mathcal{I}\\ \end{aligned} x∈Rnmin s.t. f(x)ci(x)=0,i∈Eci(x)≤0,i∈I
有如下二阶条件
定理(二阶必要条件) 设 x ∗ x^* x∗ 为问题的局部极小点,且满足 KKT 条件,设对应的 Lagrange 乘子为 λ ∗ \lambda^* λ∗,若正则化条件 2 成立,必有
p T W ∗ p ≥ 0 , ∀ p ∈ G ∗ p^T W^* p \geq 0,\forall p \in G^* pTW∗p≥0,∀p∈G∗
定理(二阶充分条件) 设 x ∗ x^* x∗ 处存在 Lagrange 乘子使得 KKT 条件成立,对应的 Lagrange 乘子为 λ ∗ \lambda^* λ∗,若条件
p T W ∗ p > 0 , ∀ p ∈ G ∗ p^TW^*p > 0, \forall p \in G^* pTW∗p>0,∀p∈G∗
成立,则 x ∗ x^* x∗ 是约束问题的严格局部极小点。
参考文献
[1] 刘红英,夏勇,周永生. 数学规划基础,北京,2012.