1.向量的外积定义

向量的外积也叫叉积。

外积的定义也有两个，如下：

假设在三维空间中（向量的叉积只能定义在三维空间中，如二维、三维），两个向量,，则

1），其中是垂直与和所组成平面的单位法向量

2）=

与向量的内积一样，为啥会有两种定义？如何验证这两种定义所给定的不同计算方式最终结果是一致的？

下面我们从几何和物理的角度分别求证一下。

2.向量外积的几何解释

我们先从二维平面开始。

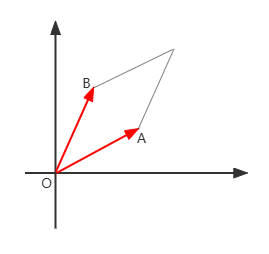
 上图中向量和构成的三角形，其面积等于图示平行四边形面积的一半。

接下来我们将向量和进行平移，如下图所示：

 通过图中的移动方式，我们将三角形的面积转换为四边形的面积

 其中，原本的，B=，我们将初始条件带入面积公式中，可以求得

即可得

而通常求取平行四边形面积的时候，如下图：

平行四边形的面积等于：

所以平行四边形面积

 接着，我们扩展到三维空间中。

 在向量叉乘的定义公式中=，所得结果在z轴上的分量是，表明外积z轴方向上的分量是由向量a和b在xoy平面上的分量计算出来的。那这个分量怎么计算？

观察上图，三维空间中向量和在xoy平面的分量是和，依据上一步二维空间向量外积的计算公式，就等于。也就是说，三维空间向量在z轴上的值就是向量a和b在xoy平面上二维投影分量的外积值。

 相同的，x轴对应着向量a和b在zoy平面上的分量，y轴对应着向量a和b在xoz平面上的分量。

那么在三维空间中，

我们如何证明的值等于向量)的值? 

简单地讲，与上一篇博客证明向量的内积的方法一样，将向量和的相交组成的平面作为x0y所在的平面，并其中任意的一个向量作为x轴，我们以以向量作为x轴，这样我们就降维，又重新回到了前面证明的二维平面上了。

从几何角度上验证了向量外积两种定义的一致性。

3.向量外积的物理解释

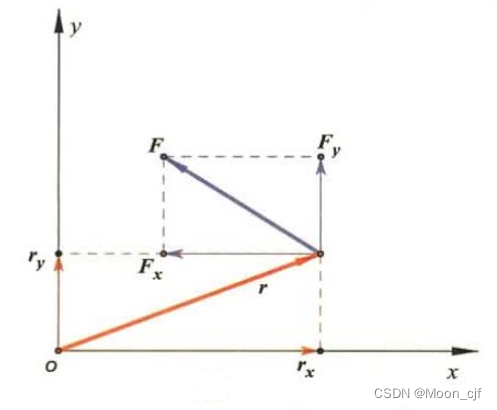
 力矩等于力臂和力的乘积，其中有效部分力臂与力的方向要垂直。

上图中力矩

注意：是向上的，是向下的。

力矩M的值等于

我们把xoy坐标系逆时针旋转一定角度，将x轴与向量重合，如上图。我们重新把力沿着新的x'轴进行力的分解，因为沿着力臂方向的分力不产生力矩，所以此时力矩

其中，

力矩M的值等于

同一个力矩使用两种角度分析，因此=

由此，我们从物理角度上验证了向量外积两种定义的一致性。