椭圆曲线密码（ECC）

ECC比RSA和经典的Diffie-Hellman等更强大、更高效——含256比特密钥的ECC比含4096比特密钥的RSA提供的安全性更强，但同时ECC也更复杂。

ECC会对大数进行乘法运算，ECC做大数乘法是为了将所有元素看作点，并将它们组合在一起，构成一条数学曲线，这条曲线被称为椭圆曲线（其实与椭圆无关）。椭圆曲线有许多不同的类型——简单的和复杂的、高效的和低效的、安全的和不安全的。
椭圆曲线可以实现经典公钥密码系统的所有功能，包括加密、签名和密钥协商等，并且它的执行速度比经典公钥密码系统更快。

椭圆曲线

椭圆曲线是平面上的曲线，曲线方程定义了所有属于曲线的点。无论曲线是什么，曲线上的点都满足曲线方程的(x,y)对。
椭圆曲线定义了这样一条曲线，这条曲线对应的方程为 （Weierstrass型），其中常数a和b决定了曲线的形状。

在密码学中使用椭圆曲线时，需要使用曲线上的点来完成加密等功能，若误用了不在曲线上的点通常会带来安全风险。

整数的椭圆曲线

在密码学中使用的曲线上的点都是整数。现在假设有一条曲线，方程为 。方程的解是模某个数n之后的计算结果（即y∈[0,n)）。
现在假设n=191，当x=3时，得 ，此时相当于 ，得到y=46或145，这些解得到的集合称为 。
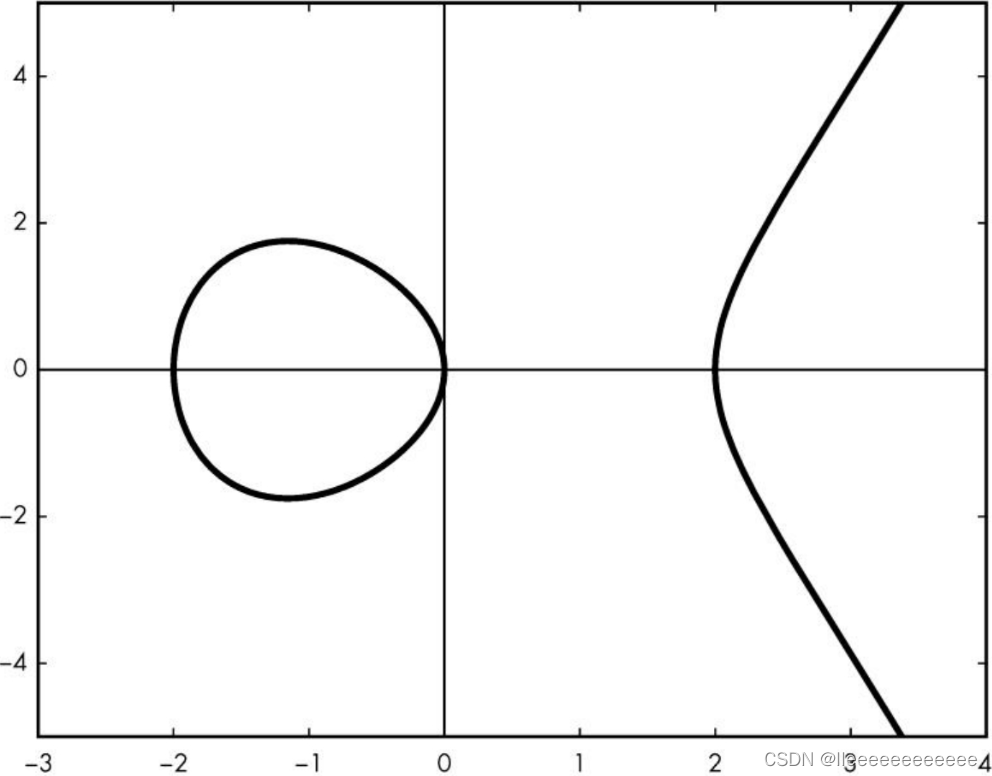
下图为 在实数域内（上）的图形和整数域内（下）的图形。
当x=3时，解得点(3,46),(3,145)在曲线上。

域和有限域

对于某个数n，按照模n定义加法和乘法的数的集合，每个元素x分别有一个关于加法的逆元（记作-x）和一个关于乘法的逆元（记作1/x），并且包含包含恒等元素0，这样的集合称为域。
例如在 中，有x+0=x，x+(-x)=0，则(100+91) mod 191=0，所以100的加法逆元是91。
有x*1=x， ，则 ，所以48的乘法逆元是4。

有限域也叫伽罗瓦域（GF），当域含有有限数量的元素时，就称该域为有限域。

加法定律

现在再来考虑 ，现在选取椭圆曲线上的两点P和Q，对两个点做加法，得到一个新的点R。
方法：作连接点P和点Q的直线，该直线与曲线相交于第三点，这一点关于x轴的反射点R即为P+Q。
下面计算R的坐标。

设P点坐标 ，Q点坐标 。R点坐标 ，则



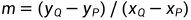
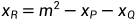
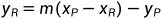
有两种特殊情况：
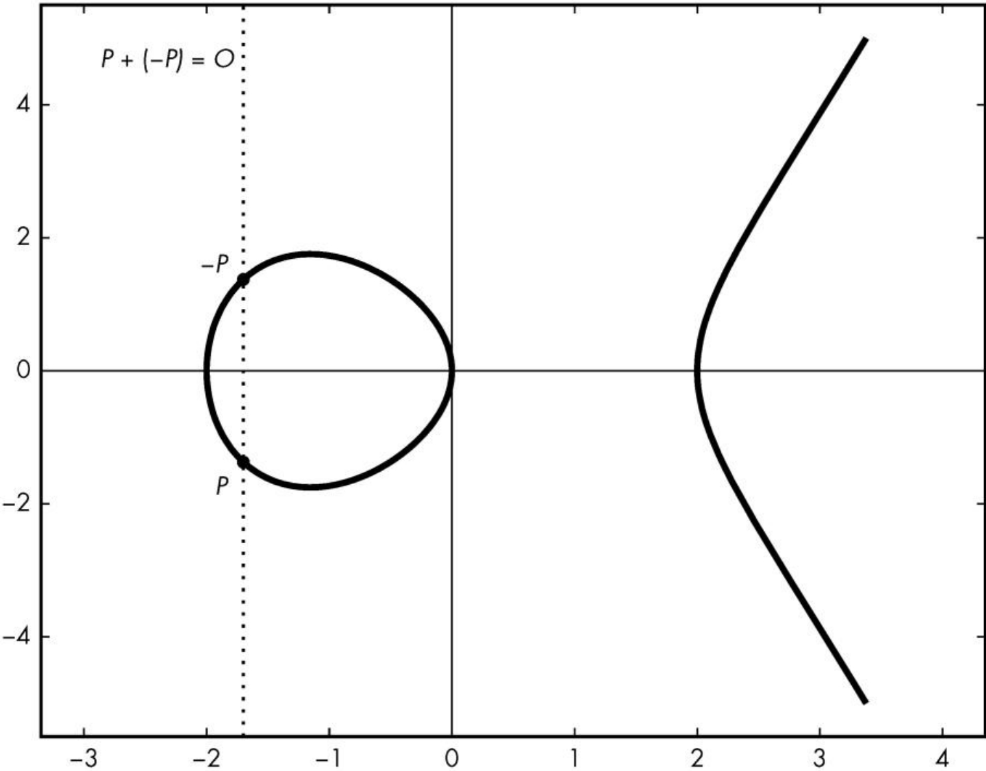
1.当Q=-P时，如下图所示，两个点与曲线不会交于第三点。此时两点互为逆元。
P+(-P)=O，其中，O被称为无穷远点，意思为连接P和–P之间的直线一直延伸到无穷远，不会与曲线相交。

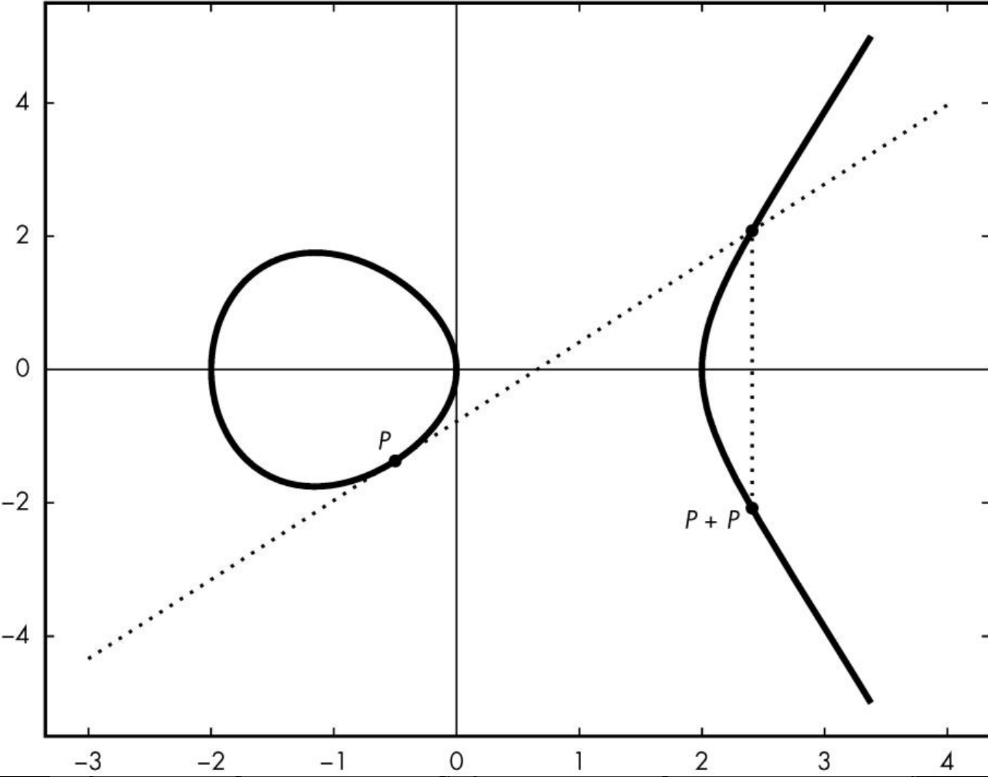
2.当Q=P时，P、Q重合，P+Q=P+P=2P,此时不能用上面的公式算出R的坐标，需要在点P处画一条曲线的切线，其中P是切点，这条切线会与曲线相交于另一点，这一交点记为R，如下图
计算公式为：
,其中a是曲线方程 的参数a,对于 来说a=-4

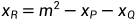
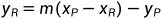
乘法定律

乘法是将曲线上的点P乘以某个数k，相当于k个P相加，即

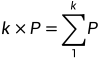
所以乘法就是按照上面的加法定律操作k-1遍。但是如果k过大，这种方法会非常慢，所以还有一种简便的方法：



......

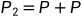
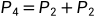
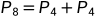
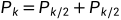
这里 即为n*P。

椭圆曲线群

椭圆曲线上的点的集合构成了群。根据群的定义，如果点P和点Q都在一个给定的曲线上，那么P+Q也在该曲线上。对于曲线上的任何三个点P、Q和R，都有(P+Q)+R=P+(Q+R)。在椭圆曲线的所有点组成的群中，无穷远点就是单位元，并被表示为O，也即对曲线上任意的点P，P+O=P始终成立。此外，点P= 还有唯一的逆元–P= ，这时就有P+(–P)=O。

曲线上的点的数量，这也被称为椭圆曲线的基数、群的阶，简称为阶。

ECDLP问题

称为椭圆曲线离散对数问题：给定一个基本点P和它的某个倍数Q=kP，求解k。
所有的椭圆曲线密码系统都建立在ECDLP问题之上。

求解k的一种方法是寻找两个输出 和 之间的碰撞。这些方程中的点P和
点Q满足Q=kP，其中数k未知，c1、d1、c2和d2是为了寻找k所需的数。
当两个不同的输入产生相同的输出时，就会发生碰撞。需要先找到满足下列方程的两个点：

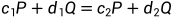
将Q=kP代入，得
,合并系数得
，这说明 = ，则
=> ，得

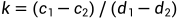
椭圆曲线的Diffie–Hellman密钥协商（ECDH）

DH:
给定一个固定的数字g，小明选择一个秘密的随机数a，并计算 ，将A发送给小王；小王选择一个秘密的随机数b并将 发送给小明。然后小明和小王将自己的私钥与对方的公钥结合起来，就可以生成相同的 。
ECDH：
在ECC中，对于某个不动点G，小明取一个秘密的随机数 ，计算 ，并将 发送给小王。小王选择一个秘密的随机数 ，计算出点 ，并将其发送给小明。然后双方据此计算相同的共享密钥 。

椭圆曲线的签名（ECDSA）

使用ECC进行签名的标准算法是ECDSA，由 签名生成算法和 验证算法组成，签名生成算法使用签名者的私钥创建签名，验证算法可以根据签名者的公钥来检查签名的正确性。签名者持有数字d作为私钥，验证者持有公钥P=dG。双方事先都知道的内容有：使用的椭圆曲线方程，椭圆曲线的阶（曲线中的点数n），以及一个基点的坐标G。

对消息M 签名的步骤：
1.先使用hash函数（如SHA-256）对消息M生成一个hash值h（h∈[0,n)），在[0,n)之间选一个随机数k并计算kG的坐标(x,y)。
2.令r=x mod n，计算s=(h+rd)/k mod n生成签名(r,s)。签名的长度取决于椭圆曲线中使用的坐标的长度。

已知签名(r,s)和hash值h，对消息M 验签的步骤：
1.计算w=1/s（s的乘法逆元），由s=(h+rd)/k 得 w=k/(h+rd) mod n。
2.计算u=wh=hk/(h+rd)，v=wr=rk/(h+rd)
3.计算点Q=uG+vP，P是签名者的公钥，P=dG，只有在Q的x坐标等于签名中的r值时才接受签名。
4.Q=uG+vdG=(u+vd)G，而u+vd=hk/(h+rd)+drk/(h+rd)=(hk+drk)/(h+rd)=k，则Q=kG，说明计算出的点与生成签名时计算的点相同。
一旦验证者确认点kG的x坐标等于接收到的r，验证就完成了；否则，签名将被视为无效而被拒绝。

椭圆曲线的加密（ECIES）

一种简单方法是使用集成加密方案（Integrated Encryption Scheme，IES）。这是一种基于Diffie-Hellman密钥交换的混合非对称-对称密钥的加密算法。本质上，IES通过生成一个Diffie-Hellman密钥对来加密消息，将私钥与接收方自己的公钥组合在一起，从获得的共享密码中派生出对称密钥，然后使用经过身份验证的密码来加密消息。这种加密称为ECIES。

给定接收方的公钥P，ECIES对消息M进行加密的步骤如下：
1．选择一个随机数d，计算点Q=dG，其中基点G是一个固定参数。这里，(d,Q)充当会话密钥对，仅用于加密M。
2．通过计算S=dP得到一个ECDH共享密钥。
3．使用密钥派生方案（KDF）从S中派生出对称密钥K。
4．使用对称密钥K和对称身份验证密码加密消息M，获得密文C和身份验证标签T。
这样，ECIES的密文由会话公钥Q加上C和T组成。解密很简单：接收方通过将R与其私有指数相乘来计算S，然后生成密钥K，利用K解密C并验证T。

曲线的选择

基于椭圆曲线的密码系统的安全性取决于它所使用的群的阶（即曲线的点数）、它的加法公式和它的参数的选取原因。
必须仔细选择曲线方程 中的系数a和b，群的阶不能等于一些小数的乘积。
一般在使用时可以选择已经被大量实例证实为安全的曲线。

目前常用的是NIST曲线中的素数曲线和Curve25519。

NIST曲线

Curve25519

Daniel J.Bernstein在2006年将Curve25519（数字分段读为25-5-19）推出。
Curve25519的方程形式为 。
Curve25519适用于模素数 的数， 是一个256比特的素数，而且尽可能接近 。b的系数486662是满足Bernstein设定的安全准则的最小整数。