运筹学有时候面临的一种场景是求最短路(shortest path)问题:比如城市交通的网络设计,芯片的表面设计等。解决这类问题常用离散动态规划(discrete dynamic)方法。今天我们就来学习这种场景以及解决的算法。
1
抽象为模型
我们用三个与现实场景十分相似的例子来介绍模型以及相关术语。
利特尔维尔交通规划
假设你是利特尔维尔城市的交通工程师,下图是该城市的市区街道规划图,图中标注了道路是单行道还是双向道,也标注了汽车通过每条街区所需要的平均时间(单位:秒).
从调查报告和其他数据中我们可以估计出出行居民的数量、出行的起点和终点,但是他们具体选择怎样的路径则不得而知。交通工程师的一项任务就是估计出居民所选择的路径,从而使得城市管理者能够估计出是否有某条道路会产生拥堵。
为了得到一个不错的初步估计,我们可以首先假设所有的出行居民都会做出理性的决策——也就是选择连接起点和终点的最短路径。因此,我们首先需要找到图中任意两点间的所有最短路径。
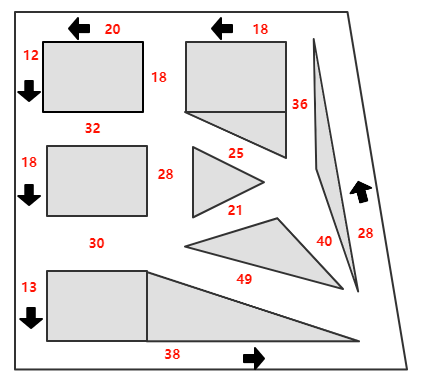
要用数学来解决这个问题,首先,先将给定的街区系统抽象为图(graph)或网络(network),图模型我们在机器学习的概率图一块给出了初步定义,在运筹学这里有稍微的不同,为了表达得清晰准确,我们定义:
节点表示网络中的实体、交点和转移点,为了方便,利特尔维尔例子的节点用1到10进行标号。节点之间可能被弧或者边相连(弧特指有方向的边),比如这里用弧表示单向街道,边表示双向街道。
利特尔维尔例子转化为图,表示如下:
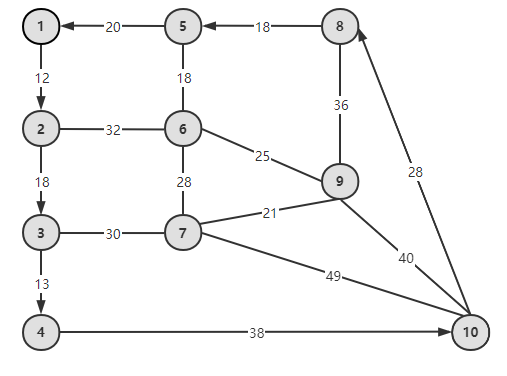
有了图,我们可以给路(path)下定义:
路是图中连接两个特定节点的一序列的弧或者边。在这个序列中,每条弧或者边与其前方的弧或者边有且只有一个共同点。在经过弧时,只能按照该条弧所标注的方向通过。同时,没有节点会被一条路重复经过。
举个例子,利特尔维尔例子中,从节点3到节点8有很多路径,比如3-7-10-8和3-4-10-8,这两条都是路。而3-7-6-5-8不是路,因为(5,8)是弧,只能8-5;3-7-6-9-7-10-8也不是路,因为重复使用了节点7.
当一个实际问题的抽象图中的弧和边涉及成本或者长度时,我们就面临一个优化问题:最短路问题就是寻找图中两节点之间总长度最短的路的问题.
利特尔维尔案例是一种最短路问题类别,它有如下基本假设:
图:弧和边
成本:非负
输出:最短路
配对方式:所有节点与其他节点
除此之外,最短路问题涉及最多的还有额外两个类别,我们分别用例子说明。
德克萨斯运输公司
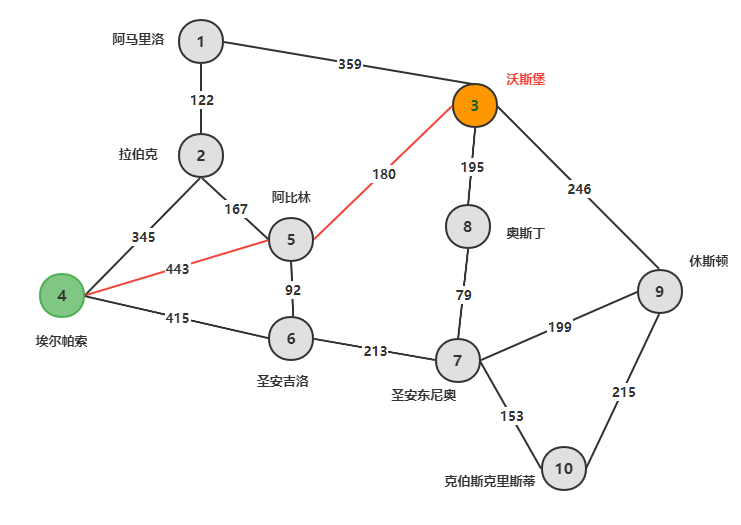
下图展示了德克萨斯州内几个重要城市的高速公路连接图,边上标记的数字代表着标准的驾驶距离(单位:英里).
德克萨斯运输公司需要将货物从位于沃斯堡的中心仓库运送到图中其他所有城市去。卡车从仓库出发并直接开往目的地,在中途不会进行货物的装卸。司机们可以自主选择从沃斯堡到目的地的路径,但会根据从起点到终点的最短路径来给司机们发工资。为了明确这个提案对公司的影响,我们需要计算出仓库到所有城市的最短路的长度。
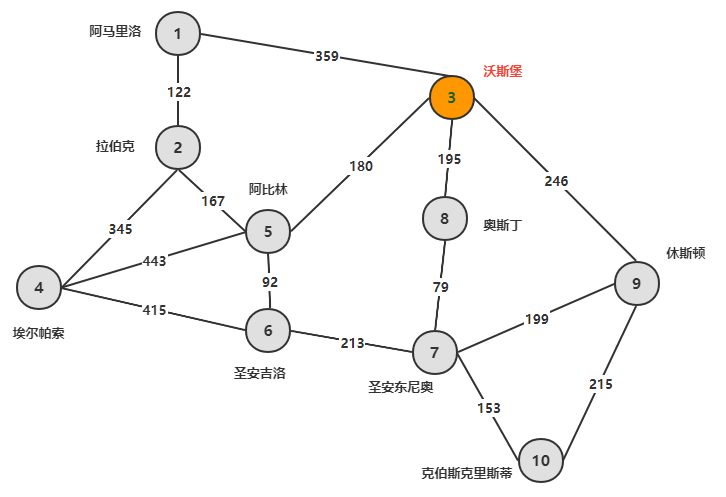
德克萨斯运输公司的基本假设有:
图:只有边
成本:非负
输出:最短路
配对方式:一个起点到其他节点
“双环”马戏团
“双环”马戏团的表演临近演出尾声。他们计划回到塔拉哈西的总部。按照目前的安排,他们最后一场演出在林肯县结束,但如果返程途径的城市有提前预定的话,仍然有可能在当地加演。下图画出了可能的返程路径以及估计出的费用(单位:千美元)。图上还标注了在该城市出演预计可以得到的收益(单位:千美元)。我们希望能求出马戏团最优的返程路线,以达到收益最大化(这里的收益在节点产生)。
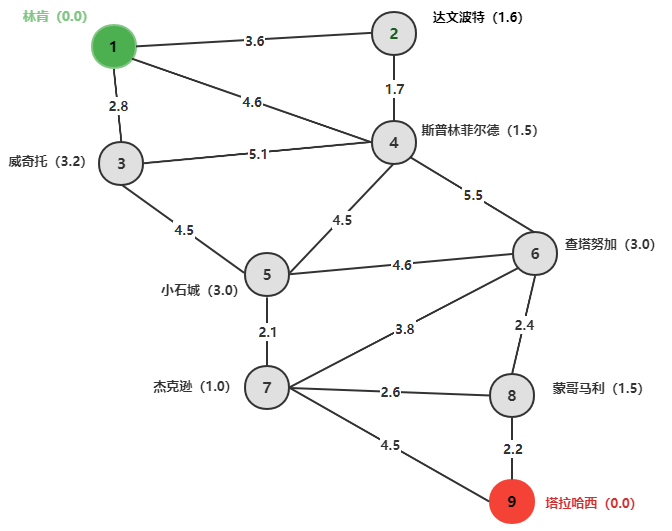
这张原始的马戏团旅行网是一张无向图,首先要处理节点的收益,必须转化为等价的有向图,再将节点的收益“转嫁”到弧上。由于两个城市之间往返的路费是一样的,因此,对应有向图为:
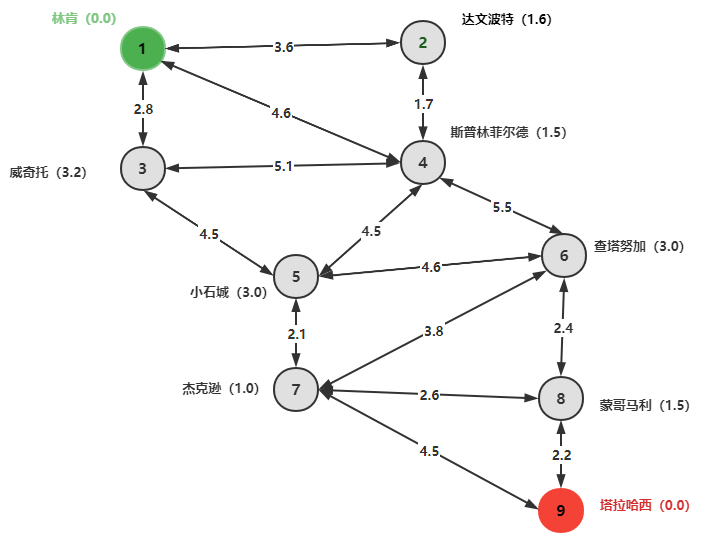
从成本出发,将节点收益转移到弧上:将弧上的成本减去弧末端所在城市的利润。合并节点的“收益”,得到从一个城市到另一个城市的成本(这时候往返成本不一样):
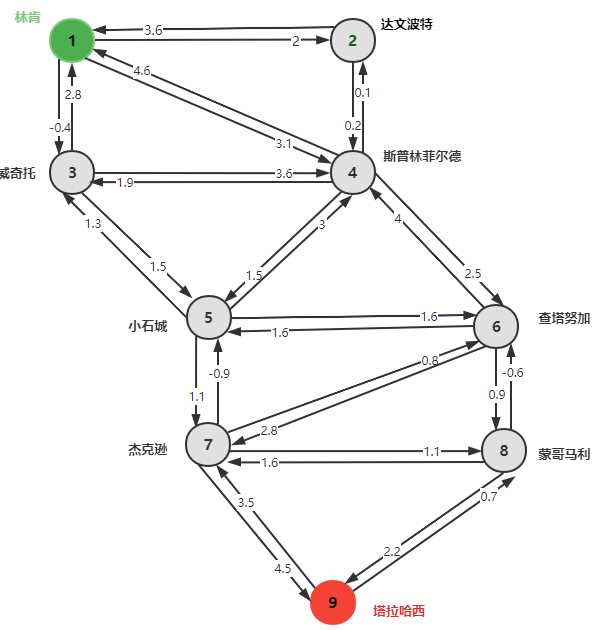
因为最短路只允许一个节点经过一次,因此这样计算的弧成本是正确的。“双环”马戏团的基本假设是:
图:只有弧(有向图)
成本:可正可负
输出:最短路
配对方式:一个起点到一个终点
上面的最短路模型可以归纳为两类:一对多和多对多最短路问题。
2
动态规划
可以利用动态规划(dynamiic programming)的方法来解决上述提到的最短路径问题。为此,需要定义一些数学符号:

为了便于理解,举个例子。考虑下图从起点1到达其他所有节点的最短路问题。
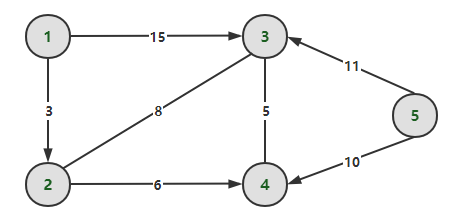
根据定义,我们可以得到每个节点的最短路长度以及路径:
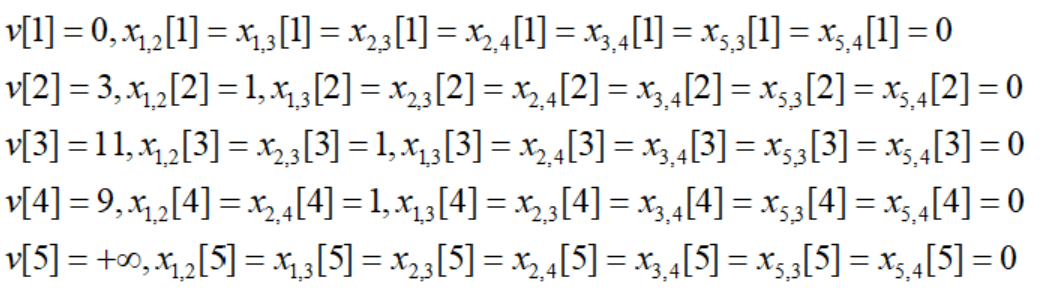
下面我们思考这个逻辑:对于德克萨斯州案例,从3到10的最短路径为3-8-7-10,这条路经过节点8和7,现在考虑从3到8的最短路,很显然只有3-7-8,不存在其他比这条更短的路,如果有,只需要沿着这条路先到达8,再到10即可,那么就会存在比原来更短从3到10的路。
因此,我们有结论:最优路径一定包含着最优的子路径(sub path)
但可惜,这个结论是有问题的。考虑下图的例子,从节点1到3的最短路是1-2-3,但从1到2的最短路是1-3-4-2.

造成这样的现象的原因在于存在负权有向环路(negative dicycle):环路指的是起点和终点重合的路,负权环路指的是总长度为负的环路.
上图的3-4-2-3就是一个负权环路,总长度为-10.但幸运的是,负权环路是最短路问题中唯一难以解决的情况,因此,上面的结论更加精准的定义为:在一个没有负权环路的图中,最优路径一定包含着最优子路径
有了这个结论,我们可以利用动态规划的函数方程(functional equation)来梳理最短路问题的递归关系。我们用两个例子来说明这种思想。
一个节点到其他节点的函数方程(一对多)
在一个没有负权环路的图中,从起点s到所有其他节点的最短路函数方程为:

以德克萨斯州运输为例子,要从3到4,经过计算比较可以得到:
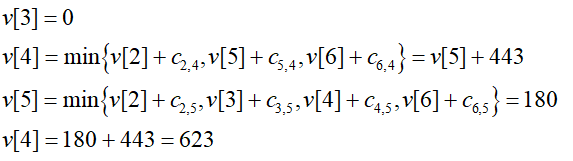
v[4]的最短路径为什么经过节点5?因为与4相连的只有节点2,5,6,若最短子路径经过节点2,那么距离只能是122+345或167+345,都比443长,节点6同样的道理,只能是5.
从所有节点到所有其他节点的函数方程(多对多)
在没有负权环路的图中,从所有节点到其他节点的最短路问题的函数方程为:

这函数方程表明,从k到l的最短路要么包含了弧/边(k,l),要么就存在一个中介点i,最优路径包含从k到i的最短路加上从i到l的最短路。
举个例子,找出下图任意两点的最短路。
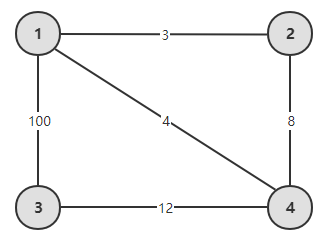
利用观察,我们得到从节点i到节点j的最短路及其路径:

然后我们利用原理得到从节点1到4和2到3的最短路:
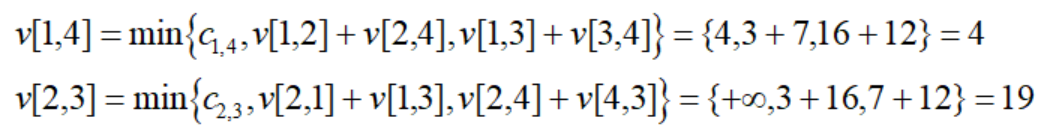
上面两个例子展现了动态函数方程的工作原理。但我们也可以发现,环路的存在会使得函数方程造成循环依赖的状况无法求解。为此,我们必须开发可以操作的算法来实现动态规划的这种思想。这些我们下一次介绍。