参考资料：

• B站 - 考研数学-积分不等式（所有方法全归纳）
• 张宇基础和强化及习题册

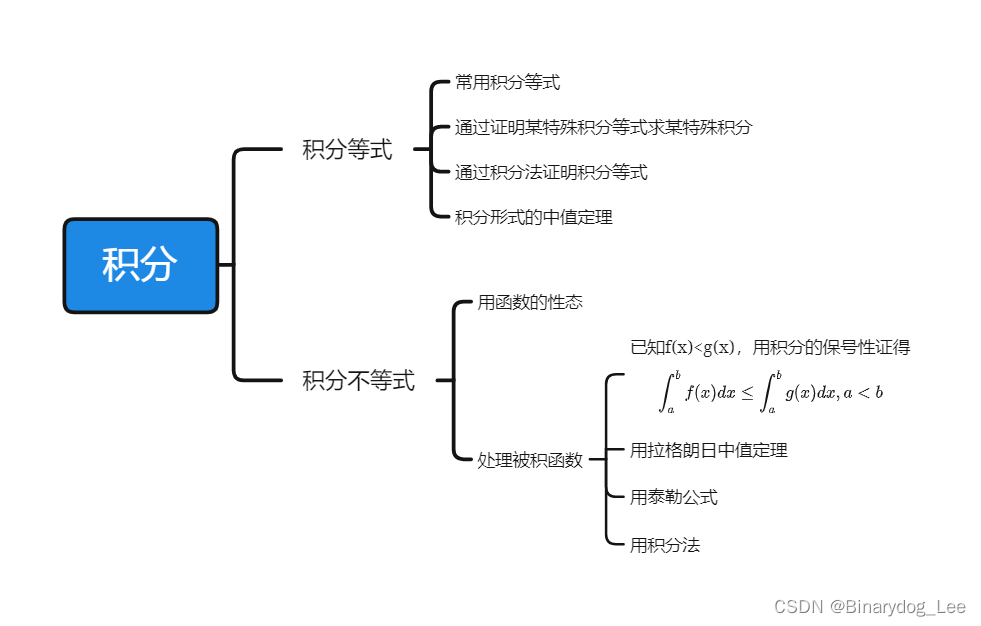
积分等式

• 中值定理
• 夹逼准则
• 积分法

在这个专题中，有如下经验：

• 遇到$f(x)$连续，应当想到变限积分${\int }_a^{x}f(t)dt$求导就是$f(x)$
• 某定积分的被积函数含有（或者就是）变限积分则考虑分部积分法
• 定积分（上下限不是变量）是一个数，所以求导是0（一个区间的积分存在是个数，有时可设为A）
• NL公式逆用：$f(x)-f(a)={\int }_a^x{f}^{\prime }(x)dx$

$${\int }_0^{\frac{\pi }{2}}f(\sin x)dx={\int }_0^{\frac{\pi }{2}}f(\cos x)dx$$

$${\int }_0^{\pi }xf(\sin x)dx=\frac{\pi }{2}{\int }_0^{\pi }f(\sin x)dx$$

中值定理

夹逼准则

先对被积函数放缩，然后对整个放缩的不等式积分得出结果。

积分法

积分不等式

函数性态（单调性）

因为要证$f(x)>a$，所以可证$F(x)=f(x)-a>0$。这意味着$F(x)$可能始终恒正，或者区间为零且单增，或者区间极小值大于0

对于条件是$f(x)$在$[a,b]$上连续的条件，通常要将某一积分限（通常是上限）变量化，然后移项构造辅助函数$F(x)$，基于$F(x)$的单调性证明不等式、

在$[a,b]$上连续也是判断要使用这个手段的一个特征。

最后求出$F^{\prime }(x)$可能是这样的形式$F^{\prime }(x)={\int }_a^{b}f(x)dx+cf(x)$，此时应当利用积分中值定理将之统一成积分或者函数。而积分+函数的形式不好处理。

拉格朗日中值定理

多用于$f(x)$一阶可导且某一端点值较为简单（甚至为0）的题目

泰勒公式

多用于$f(x)$二阶可导且某一端点值较为简单（甚至为0）的题目

积分法

利用分部积分法反向证明，不断把高阶导数变为低阶导数直至原函数$f(x)$

习题回顾

利用罗尔定理

张宇基础30讲T10.1

在明确了使用函数性态后等式移项得到要确定$\exists x$使$G(x)=0$存在，构造回原函数$F(x)={\int }_a^{x}f(t)dt{\int }_x^{b}f(t)dt$，利用罗尔定理，此时有$F^{\prime }(x)=G(x)$，利用罗尔定理确定存在。

变限积分${\int }_a^{x}f(t)dt$求导就是$f(x)$

300 T10.4

先积分中值定理再罗尔

含反函数项的处理

本例来自张宇基础30讲T10.2

考点：

1. 如果一个函数$f(x)$具有反函数$g(x)$，则对于任意的$x$在定义域内，有$f(g(x))=x$成立
2. 某定积分的被积函数含有（或者就是）变限积分则考虑分部积分法

它先分部积分法，将那个把函变限积分的当做$u$，然后$\int udv=uv-\int vdu$，然后$du$相当于对变限积分求导，把上限（本题上限是反函数）弄掉了。然后又来了一遍分部积分（这一步类似T8.5）

泰勒公式

张宇基础300题T10.9

本题求的是${\int }_0^{1}f(x)dx\ge 1$，但是仅有的条件是$f(\frac{1}{2})=1$和$f^{\prime \prime }(x)>0$，碰到二阶导（高阶导）想到分部积分法和泰勒公式。目测分部积分法不行，故考虑泰勒公式，展开已知的$f(\frac{1}{2})=1$到余项为二阶导的深度即可。

$$f(x)=f(x_0)+f^{\prime }(x_0)(x-x_0)+\frac{f^{\prime \prime }(\xi )}{2!}(x-x_0{)}^2$$

去掉余项之后（且$f(x_0)=1$，因为$x_0=\frac{1}{2}$）

$$f(x)>f(x_0)+f^{\prime }(x_0)(x-x_0)$$

两侧积分，过程如下，证毕

$${\int }_0^{1}f(x)dx>{\int }_0^1[1+f^{\prime }(x_0)(x-\frac{1}{2})]dx=1+f(\frac{1}{2}){\int }_0^1(x-\frac{1}{2})dx=1$$

绝对值不等式

张宇基础300题T10.7

利用$f(x)=f(x)-f(a)={\int }_a^x{f}^{\prime }(x)dx$得到：

$$|f(x)|=|{\int }_a^x{f}^{\prime }(x)dx|\le {\int }_a^x|f^{\prime }(x)|dx$$

同理$f(x)=f(x)-f(b)={\int }_b^x{f}^{\prime }(x)dx$，则有：
$$|f(x)|=|{\int }_b^x{f}^{\prime }(x)dx|\le {\int }_x^b|f^{\prime }(x)|dx$$

注意这一次$x$在积分下限，因为$x<b$，在$|f^{\prime }(x)|\ge 0$的情况下，如果$b$是下限则会导致积分是负的。

二式合一得到$2|f(x)|\le {\int }_a^x|f^{\prime }(x)|dx+{\int }_x^b|f^{\prime }(x)|dx$即

常数设为A

300 T10.2

$f(x)=\frac{x}{1+{\cos }^{2}x}+{\int }_{-\pi }^{\pi }f(x)\sin xdx$求$f(x)$，思路是设$A={\int }_{-\pi }^{\pi }f(x)\sin xdx$，则有$f(x)=\frac{x}{1+{\cos }^{2}x}+A$。然后$f(x)\sin x=g(x,A)sinx$并求积分，利用被积函数的奇偶性消去一项，然后求解出$A=\frac{{\pi }^2}{2}$，代回原先的$A={\int }_{-\pi }^{\pi }f(x)\sin xdx$即可

切不可因为

$${\int }_{-\pi }^{\pi }f(x)\sin xdx=A={\int }_{-\pi }^{\pi }\frac{x\sin x}{1+{\cos }^{2}x}$$

就认为$f(x)=\frac{x}{1+{\cos }^{2}x}$