一,基本概念
1.定义:动态规划实际上是一类题目的总称,并不是指某个固定的算法,其意义是通过采用递推或分而治之的策略,通过解决大问题的子问题从而解决整体的做法,核心思想是巧妙地将问题拆分成多个子问题,通过计算子问题而得到整体问题的解,而子问题又可以拆分成更多的子问题,从而用类似递推迭代的方法解决要求的问题
2.与分治法最大的差别是:适合于用动态规划法求解的问题,经过分解后得到的子问题往往不是独立的(即下一个子阶段的求解是建立在上一个子阶段的解的基础上,进行进一步的求解)
3.解题的核心分为两步:
第一步:状态的定义,有的问题过于抽象或者过于啰嗦干扰我们解题思路,我们要做的就是将题干中的问题进行转化(换一种说法,含义不变),eg,
题目:求一个数列中最大连续子序列的和我们将这个原问题转化为:
Fk是第k项的最大子序列的和,求F1—Fn中最大值第二步:状态转移方程的定义,即如何去求解一个问题,对于上述已经转换成的问题,关注点在于,如何能够用前一项或者前几项的信息得到下一项,这种从最优子状态转换为下一个最优状态的思路就是动态规划的核心,对于上例子,状态转移方程即是
Fk=max{Fk+Ak,Ak}
Fk是前k项的和,Ak是第k项的值4.应用场景
从上述可以得出,动态规划不是某个固定的算法,而是一种策略思路,那么什么时候应该去使用什么时候不能用?
对于一个可拆分问题中存在可以由前若干项计算当前项的问题可以由动态规划计算,能用动态规划计算的问题存在一种递推的连带关系二,常见动态规划问题
1.国王和金矿
题目:有一个国家发现了5座金矿,每座金矿的黄金储存量不同,需要参与与挖掘的工人数也不同,参与挖掘工人的总数是10人,每座金矿要么全挖要么不挖,不能派出一半人挖取一半金矿,要求获得尽可能多的黄金,应该选择哪几座金矿?
金矿分布及工人要求:400金/5人、500金/5人、200金/3人、300金/4人、350金/3人
分析:动态规划的三个核心元素:最优子结构,边界,状态转移方程式
方法一:排列组合,每一座金矿都有挖和不挖两种选择,如果n座金矿,就有2^n中选择,对所有可能性做遍历,排除那些使用工人数超过10的选择,在剩下的选择里找出获得金数量最多的,时间复杂度为O(2^n)
动态规划
最优子结构:10个工人4个金矿时挖出黄金最多,(10-第5金矿需工人)工人4个金矿时挖出的黄金最多
最优选择即:10工人4金矿的数量,和,(10-第5金矿需工人)工人4个金矿时挖出的黄金+第5座数量,最大值
设金矿数量为n,工人数量为w,金矿黄金量为数组g[],金矿用工量为数组p[],则最优选择用表达式描述为
F(5,10)=max(F(4,10), F(4,10-p[4])+g[4])
边界:n=1, w<p[0]时,F(n,w)=0,给的工人不够挖一个金矿,得到为0
n=1, w>=p[0]时,F(n,w)=g[0],只有一个金矿且工人足够,那么只能挖这一个金矿
总结就是:
F(n,w)=0, (n<=1,w<p[0])
F(n,w)=g[0], (n==1,w>=p[0])
F(n,w)=F(n-1,w), (n>1,w<p[n-1])
F(n,w)=max{F(n-1,w),F(n-1,w-p[n-1]}+g[n-1], (n>1, w>=p[n-1])方法二:简单递归
将状态转移方程式翻译成递归程序,递归结束的条件就是方程式当中的边界,因为每个状态由两个最优子结构,所以递归的执行流程类似于一棵高度为n的二叉树,时间复杂度为O(2^n)
方法三:备忘录算法
在简单递归的基础上增加一个HashMap备忘录,存储中间结构,HashMap的key是一个包含金矿数n个工人数w的对象,value是最优选择获得的黄金数,时间复杂度和的空间复杂度相同,都是备忘录中不同key的数量
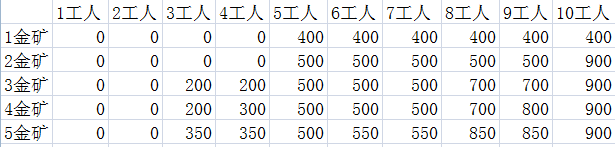
通过表格进行分析
规律:根据前一行的结果就可以推出行的一行
方法时间复杂度为O(n*w),空间复杂度为O(w)
2.数塔取数问题
问题:一个高度为n的由正整数组成的三角形,从上走到下,求经过的数字和的最大值,每次只能走到下一层相邻的数上,例如:从第三层的6向下走,只能走到第四层的2或者9上
示例:输入为(应该呈三角形,排版问题导致,请忽略)
5
8 4
3 6 9
7 2 9 5输出:28
最优方案是:5+8+6+9=28
状态定义:Fi,j是第i行j列最大取数和,求第n行Fn,m中的最大值(0<m<n)
状态转移方程:
Fi,j=max{Fi-1,j-1,Fi-1,j}+Ai,jpackage DTGH;
import java.util.Scanner;
public class Triangle {
public static long triangleMax(){
Scanner in=new Scanner(System.in);
int n=in.nextInt();//先输入一个数字表示测试数据为几行
long max=0;
int [][] dp=new int [n][n];
dp[0][0]=in.nextInt();
for(int i=1;i<n;i++){
for(int j=0;j<=i;j++){
int num=in.nextInt();
if(j==0){
dp[i][j]=dp[i-1][j]+num;
}
else{
dp[i][j]=Math.max(dp[i-1][j-1], dp[i-1][j])+num;
}
max=Math.max(dp[i][j], max);
}
}
return max;
}
public static void main(String[] args) {
// TODO Auto-generated method stub
System.out.println(triangleMax());
}
}运行结果
4
5
8 4
3 6 9
7 2 9 5
283.编辑距离
题目:编辑距离指两个字串之间,由一个转成另一个所需要的最少编辑操作次数,许可的编辑操作包括将一个字符替换成另一个字符、插入一个字符、删除一个字符,给出两个字符串a和b,求a和b的编辑距离
eg:将kitten转为sitting:
sitten(k->s), sittin(e->i), sitting(g),输出为3
状态定义:Fi,j表示第一个字符串的前i个字母和第二个字符串的前j个字母需要编辑的次数,求Fn,m,n和m分别是两个字符串的长度
状态转移方程:
当Fi,j-1=Fi-1,j时,Fi,j=Fi,j-1
当Fi,j-1!=Fi-1,j时,Fi,j=min{Fi-1,j-1,Fi,j-1,Fi-1,j}+1package DTGH;
import java.util.Scanner;
public class EditDistance {
public static int solution(){
Scanner in=new Scanner(System.in);
String a=in.nextLine();
String b=in.nextLine();
int alen=a.length();
int blen=b.length();
int [][]dp=new int[alen+1][blen+1];
for(int i=0;i<alen+1;i++){
dp[i][0]=i;
}
for(int j=0;j<blen+1;j++){
dp[0][j]=j;
}
for(int i=1;i<alen+1;i++){
for(int j=1;j<blen+1;j++){
if(a.charAt(i-1)==b.charAt(j-1)){
dp[i][j]=dp[i-1][j-1];
}
else{
dp[i][j]=Math.min(dp[i-1][j-1], Math.min(dp[i-1][j], dp[i][j-1]))+1;
}
}
}
return dp[alen][blen];
}
public static void main(String[] args) {
// TODO Auto-generated method stub
System.out.println(solution());
}
}
kitten
sitting
34.走方格问题
题目:有一个矩阵,它的每个格子有一个权值,从左上角格子开始每次只能向右或者向下走,最后到达右下角位置,路径上所有数字累加起来就是路径和,返回所有的路径中最小的路径和
分析:对于右下角的位置来说,来自于上一个向右走或者上一个向下,若设dp[n][m]为走到n*m位置的路径长度,
那么dp[n][m]=min{dp[n][m-1], dp[n-1][m]}
eg:{[1,2,3] [1,1,1]},2,3,输出4
public class Rectangle {
// n*m矩阵,从左上角走到右下角,同一时间只能向下或者向右
// dp[n][m]为走到n*m的路径长度
public static int minPathSum(){
Scanner in=new Scanner(System.in);
int n=in.nextInt();
int m=in.nextInt();
int [][]a=new int [n][m];
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
a[i][j]=in.nextInt();
}
}
int [][]dp=new int[n][m];
dp[0][0]=a[0][0];
for(int i=1;i<m;i++){//边界,第0行
dp[0][i]=a[0][i]+dp[0][i-1];
}
for(int i=1;i<n;i++){//边界,最右列
dp[i][0]=a[i][0]+dp[i-1][0];
}
for(int i=1;i<n;i++){
for(int j=1;j<m;j++){
dp[i][j]=Math.min(dp[i-1][j], dp[i][j-1])+a[i][j];
}
}
return dp[n-1][m-1];
}
public static void main(String[] args) {
// TODO Auto-generated method stub
System.out.println(minPathSum());
}
}持续更新。。。
参考:https://blog.csdn.net/QuinnNorris/article/details/77484573
https://blog.csdn.net/p10010/article/details/50196211
https://zhuanlan.zhihu.com/p/31628866