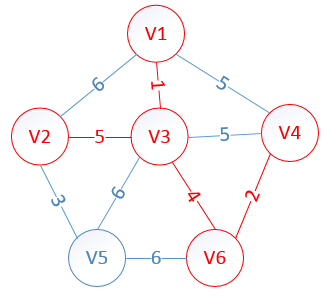
MST(Minimum Spanning Tree,最小生成树)问题有两种通用的解法,Prim算法就是其中之一,它是从点的方面考虑构建一颗MST,大致思想是:设图G顶点集合为U,首先任意选择图G中的一点作为起始点a,将该点加入集合V,再从集合U-V中找到另一点b使得点b到V中任意一点的权值最小,此时将b点也加入集合V;以此类推,现在的集合V={a,b},再从集合U-V中找到另一点c使得点c到V中任意一点的权值最小,此时将c点加入集合V,直至所有顶点全部被加入V,此时就构建出了一颗MST。因为有N个顶点,所以该MST就有N-1条边,每一次向集合V中加入一个点,就意味着找到一条MST的边。
用图示和代码说明:
初始状态:
设置2个数据结构:
lowcost[i]:表示以i为终点的边的最小权值,当lowcost[i]=0说明以i为终点的边的最小权值=0,也就是表示i点加入了MST
mst[i]:表示对应lowcost[i]的起点,即说明边<mst[i],i>是MST的一条边,当mst[i]=0表示起点i加入MST
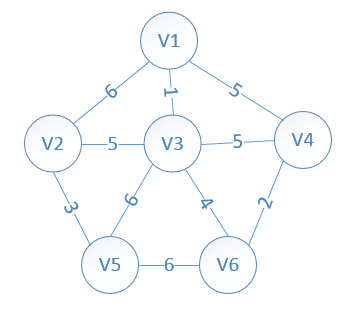
我们假设V1是起始点,进行初始化(*代表无限大,即无通路):
lowcost[2]=6,lowcost[3]=1,lowcost[4]=5,lowcost[5]=*,lowcost[6]=*

mst[2]=1,mst[3]=1,mst[4]=1,mst[5]=1,mst[6]=1,(所有点默认起点是V1)
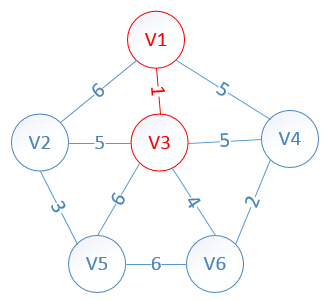
明显看出,以V3为终点的边的权值最小=1,所以边<mst[3],3>=1加入MST
此时,因为点V3的加入,需要更新lowcost数组和mst数组:
lowcost[2]=5,lowcost[3]=0,lowcost[4]=5,lowcost[5]=6,lowcost[6]=4
mst[2]=3,mst[3]=0,mst[4]=1,mst[5]=3,mst[6]=3
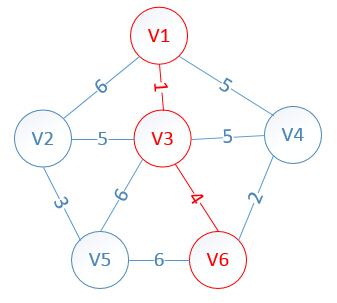
明显看出,以V6为终点的边的权值最小=4,所以边<mst[6],6>=4加入MST
此时,因为点V6的加入,需要更新lowcost数组和mst数组:
lowcost[2]=5,lowcost[3]=0,lowcost[4]=2,lowcost[5]=6,lowcost[6]=0
mst[2]=3,mst[3]=0,mst[4]=6,mst[5]=3,mst[6]=0
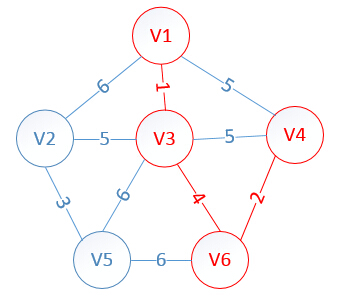
明显看出,以V4为终点的边的权值最小=2,所以边<mst[4],4>=4加入MST
此时,因为点V4的加入,需要更新lowcost数组和mst数组:
lowcost[2]=5,lowcost[3]=0,lowcost[4]=0,lowcost[5]=6,lowcost[6]=0
mst[2]=3,mst[3]=0,mst[4]=0,mst[5]=3,mst[6]=0
明显看出,以V2为终点的边的权值最小=5,所以边<mst[2],2>=5加入MST
此时,因为点V2的加入,需要更新lowcost数组和mst数组:
lowcost[2]=0,lowcost[3]=0,lowcost[4]=0,lowcost[5]=3,lowcost[6]=0
mst[2]=0,mst[3]=0,mst[4]=0,mst[5]=2,mst[6]=0
很明显,以V5为终点的边的权值最小=3,所以边<mst[5],5>=3加入MST
lowcost[2]=0,lowcost[3]=0,lowcost[4]=0,lowcost[5]=0,lowcost[6]=0
mst[2]=0,mst[3]=0,mst[4]=0,mst[5]=0,mst[6]=0
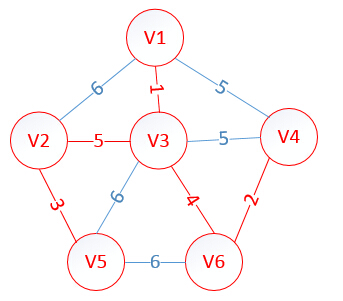
至此,MST构建成功,如图所示:
根据上面的过程,可以容易的写出具体实现代码如下
#include<iostream>
using namespace std;
#define MAX 100
#define MAXCOST 0x7fffffff
int graph[MAX][MAX];
int prim(int graph[][MAX], int n)
{
int lowcost[MAX];//i-max的距离
int mst[MAX];//表示i的起点是谁
int i, j, min, minid, sum = 0;
for (i = 2; i <= n; i++)
{
lowcost[i] = graph[1][i];
mst[i] = 1;
}//默认起点是1
mst[1] = 0;
for (i = 2; i <= n; i++)
{
min = MAXCOST;
minid = 0;
for (j = 2; j <= n; j++)
{
if (lowcost[j] < min && lowcost[j] != 0)
{
min = lowcost[j];
minid = j;
}
}//找出距离1最近的点
cout << "V" << mst[minid] << "-V" << minid << "=" << min << endl;
sum += min;
lowcost[minid] = 0;
for (j = 2; j <= n; j++)
{
if (graph[minid][j] < lowcost[j])
{
lowcost[j] = graph[minid][j];
mst[j] = minid;
}
}//相当于利用mind作为新的起点来更新lowcost[];
}
return sum;
}
int main()
{
int i, j, k, m, n;
int x, y, cost;
cin >> m >> n;//m=顶点的个数,n=边的个数
//初始化图G
for (i = 1; i <= m; i++)
{
for (j = 1; j <= m; j++)
{
graph[i][j] = MAXCOST;
}
}
//构建图G
for (k = 1; k <= n; k++)
{
cin >> i >> j >> cost;
graph[i][j] = cost;
graph[j][i] = cost;
}
//求解最小生成树
cost = prim(graph, m);
//输出最小权值和
cout << "最小权值和=" << cost << endl;
return 0;
}
Input:
6 10
1 2 6
1 3 1
1 4 5
2 3 5
2 5 3
3 4 5
3 5 6
3 6 4
4 6 2
5 6 6
Output:
V1-V3=1
V3-V6=4
V6-V4=2
V3-V2=5
V2-V5=3
最小权值和=15