最小生成树概述

　　最小生成树（Minimum Spanning Trees），简称MST。是图论中一个非常重要的概念。解决这个问题有两种算法，今天暂且先来讨论一下Prim Algorithm。不做特别说明，讨论的都是无向图。

　　最小生成树的算法，解决的问题是一个有 n 个结点的连通的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。最小生成树可以用kruskal（克鲁斯卡尔）算法或prim（普里姆）算法求出。

思路

专业描述

将顶点集 V 分成两个集合 A 和 B，其中集合 A 表示目前已经在MST中的顶点，而集合 B 则表示目前不在 MST 中的顶点。

寻找与集合 A 连通的最短的边 (u,v)，将这条边加入最小生成树中。（此时,与(u,v) 相连的顶点，不妨设为 Bi，也应加入集合 A 中）重复第二步，直至集合 B 为空集。

例子

下面举出一个具体例子作为算法的思路展现：

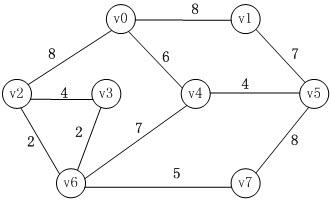
这样的一个图，要求输出联通所有vi的最短路的路径之和，怎么做？

先随意取一个点（这里取得是v0），找出所有与之相关的路径，选出最短的一条

选定这个点之后，将这个点涂上绿色，表示这个点已经被访问过了

然后，我们将v0，v4看成一个点，找与这个点相连的线段

（图中蓝色部分即为所有与这个新的“点”相连的线段）

选出最小的一条，连接，标上绿色，再将v5，v4，v0看为一个点

重复以上操作

注意：当我们发现最短的路连接的两个点都是绿色或都是黑色时，我们不选，因为这个路径“在一个点外”或“在一个点内”，即这个线段是不可取的或是多余的，例如v2和v3这种情况。

直到所有的点全部变为绿色，停止。

下面我们来看一看代码是如何实现的：

实现

int prim(int n)
{
	int ans=0;
	vis[n]=true;
	for(int i=1;i<=n;i++)
		lowc[i]=cost[n][i];
	for(int i=0;i<n-1;i++)
	{
		int minn=INF,idx;
		for(int j=1;j<=n;j++)
			if(!vis[j] && minn>lowc[j])
			{
				minn=lowc[j];
				idx=j;
			}
		if(minn==INF)
			return -1;
		ans+=minn;
		vis[idx]=true;
		for(int j=1;j<=n;j++)
			if(lowc[j]>cost[idx][j])
				lowc[j]=cost[idx][j];
	}
	return ans;
}

各种定义

vis数组就是我们标绿色圆圈的东西，表示这个节点是否被访问过了，如果被访问过了，那么vis[i]=true，如果没有vis[i]=false

cost[i][j]=w表示的是从i-j这条路径权值为w如果这两个点之间没有路径，那么cost[i][j]=INF

lowc表示蓝色的线段，即可以选择的线段

详细解析

 prim的算法很短，很好理解，我们逐个来分析。

vis[n]=true;

　这个是标记第一个点，这里我们从vn开始标记

for(int i=1;i<=n;i++)
		lowc[i]=cost[n][i];

 　　然后将所有与n相连的线段放入low数组中