https://www.luogu.org/problemnew/show/P1006
先放题
Description
题意很好理解
我们可以把它转化成这样
甲从原点开始,乙也从原点开始,找两条权值最大的路,两条路不能有重合的部分
方向只能向右或向下
这就是一个多进程的dp
我们可以考虑dp方程了
一般就会定为4维 dp[i1][j1][i2][j2] 表示甲走到了i1,j1,乙走到了 i2 j2,能获得的最大价值
看到题目,可以从题目性质考虑一下
它的递推是斜着的
于是可以斜着考虑
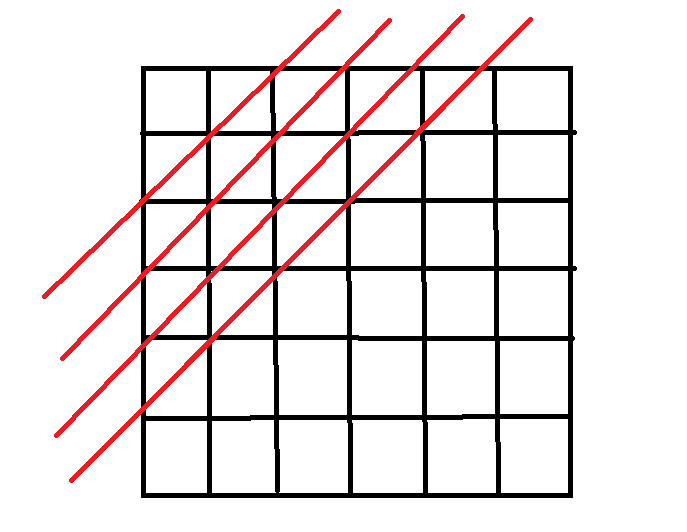
每一个状态是由上一条斜线递推出来的
于是
dp方程就可以得出来了
dp[k][i][j]=max(max(dp[k-1][i-1][j],dp[k-1][i][j-1]),max(dp[k-1][i-1][j-1],dp[k-1][i][j]))+d[i][k-i]+d[j][k-j];
k表示一条斜线上的点,因为它的横纵坐标之和是个定值,所以可以用横纵坐标之和表示第一维
第二维表示甲已经走到了第i行
第三维表示乙已经走到了第j行
压了一维之后甲的纵坐标是可以求出来的 就是k-i
乙的纵坐标也可以得出 是 k-j
我们就可以写这个题了
注意
1.一开始将dp赋初值为-1,表示所有点不可达
dp[2][1][1]=0;
2.因为递推时有很多状态是到达不了的,于是就可以continue
最后输出dp[n+m-1][n-1][n]这个值就行了,因为相当于
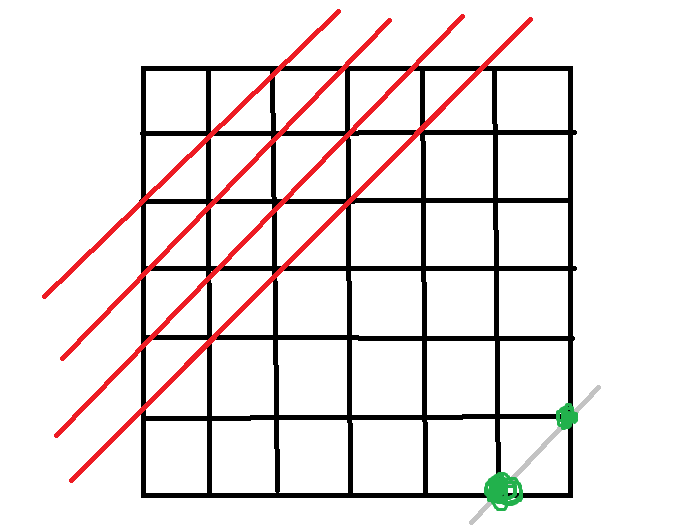
这里的两个绿点,反正最后一个点的权值为0
上代码
1 #include <cstdio> 2 #include <cstdlib> 3 #include <iostream> 4 #include <algorithm> 5 #include <cstring> 6 using namespace std; 7 const int N=60; 8 int d[N][N],dp[5*N][N][N]; 9 int n,m; 10 int main() 11 { 12 scanf("%d %d",&n,&m); 13 for(int i=1;i<=n;i++) 14 for(int j=1;j<=m;j++) 15 { 16 scanf("%d",&d[i][j]); 17 } 18 memset(dp,-1,sizeof(dp)); 19 dp[2][1][1]=0; 20 for(int k=3;k<n+m;k++) 21 for(int i=1;i<n;i++) 22 { 23 for(int j=i+1;j<=n;j++) 24 { 25 dp[k][i][j]=max(max(dp[k-1][i-1][j],dp[k-1][i][j-1]),
max(dp[k-1][i-1][j-1],dp[k-1][i][j])); 26 if(dp[k][i][j]==-1) 27 continue; 28 dp[k][i][j]+=d[i][k-i]+d[j][k-j]; 29 } 30 } 31 printf("%d\n",dp[n+m-1][n-1][n]); 32 }
这题就不愉快的解决了