数据分析

Lesson 4 : 统计学

描述性统计学 - 第一部分

数据类型

数值类型
- 数值数据采用允许我们执行数学运算（例如计算狗的数量）的数值。
分类数据
- 分类数据用于标记一个群体或一组条目（例如狗的品种 —— 牧羊犬、拉布拉多、贵宾犬等）

定序和定类

分类定序和分类定类
- 我们可以进一步将分类数据分为两类: 定序与定类。
  
  分类定序数据有排名顺序（例如与狗的互动从很差到很好排序）。
  
  分类定类数据没有排序或排名（如狗的品种）。

连续和离散数据

我们可以将数值数据视为连续或离散的。

连续数据可以分为更小的单位，并且仍然存在更小的单位。一个例子就是狗的年龄 - 我们可以以年、月、日、小时、秒为单位测量年龄，但是仍然存在可以与年龄关联的更小单位。

离散数据仅采用可数值。我们互动的狗的数量就是离散数据类型的一个例子。

数据类型
数值:	连续	离散
	身高、年龄、收入	书中的页数、院子里的树、咖啡店里的狗

分类:	定序	定类
	字母成绩等级、调查评级	性别、婚姻状况、早餐食品

数值和分类

数值可以进一步分为连续与离散。

分类数据可以分为定序与定类。

总结

数值与分类
- 其中一些可能有点棘手 —— 虽然邮政编码是一个数字，但它们并非数值变量。如果我们将两个邮政编码加在一起，并不会从得到的新值中获得任何有用的信息。因此，这是一个分类变量。
- 身高、年龄、书中的页数和年收入采用的值我们可以进行加、减和执行其他运算，来获得有用的见解。因此，这些是数值数据。
- 性别、字母成绩等级、早餐类型、婚姻状态和邮政编码可以视为一组物品或个人的标签。因此，它们是分类数据。
连续和离散
- 要区分我们的数据是连续还是离散的，要看我们是否能将数据分割成更小的单元。想想时间 —— 我们可以用年、月、日、小时、分钟或秒来衡量一个事件，甚至是在秒级，我们知道仍然有更小的单位可以用来衡量时间。因此，我们知道此数据类型为连续的。身高、年龄和收入都是连续数据的例子。或者，我们知道书中的页数、我数的咖啡店外的狗数量或院子里的树为离散数据。我们可不想将狗一分为二。
定序与定类
- 在看定类变量时，我们发现性别、婚姻状态、邮政编码和早餐食品为定类变量，这种类型的数据没有相关的顺序排列。无论你早餐吃麦片粥、吐司、鸡蛋还是只喝咖啡，它并没有相关的排序。
  
  相反，字母成绩等级或调查评级作为定序数据具有关联的排序。如果获得 A，它高于 A-。A- 的排名高于 B+，以此类推……定序变量在评级量表上很常见。在很多情况下，我们将这些定序变量变为数字，这样可以更容易地进行分析。

集中趋势测量

分析数值数据
- 分析数值数据有四个主要方面。
  1. Center 集中趋势测量
  2. Spread 离散程度测量
  3. Shape 数据的形状
  4. Outliers 异常值
分析分类数据
- 尽管视频中并未讨论，但分析分类数据要考虑的部分较少。分类数据的分析方法通常是查看落入每个组的独立个体的数量或比例。例如，如果我们在看狗的品种，我们会关心每个品种有多少只狗，或者每个品种的狗的比例如何。
集中趋势测量
- 集中趋势测量的方式有三种:
  1. Mean 均值
  2. Median 中位数
  3. Mode 众数
均值（mean）
- 均值在数学中通常称为平均数或预期值。我们通过将所有值相加，然后除以数据集中所有测量值的个数来计算均值。
中位数（median）
- 中位数将我们的数据分为两部分，一半低于它，一半高于它。我们在此视频中发现，如何计算中位数取决于我们有偶数个还是奇数个观察值。
- 奇数个值的中位数
  
  如果我们有奇数个观察值，中位数直接是中间的那个数字。例如，如果我们有 7 个观察值并按从小到大排列，则中位数是第四个值。如果我们有 9 个观察值，则中位数是第五个值。
- 偶数个值的中位数
  
  如果我们有偶数个观察值，中位数是中间两个值的平均值。例如，如果我们有 8 个观察值并从小到大排列，则计算第四和第五个值的平均值。
- 要计算中位数，我们必须首先对值排序。
- 我们使用平均数还是中位数来描述数据集，很大程度上取决于我们数据集的形状以及是否有任何异常值。

众数（mode）

众数指一组数据中出现次数最多的数据值。

一个数据集中可能有多个众数，也可能没有众数。
无众数
- 如果数据集中的所有值出现的频数相同，则不存在众数。如果我们有一组数据集：
  
  1, 1, 2, 2, 3, 3, 4, 4
  
  则没有众数，因为所有观察值发生的次数相同。
多个众数
- 如果两个（或多个）数字出现的次数都是最多的，则有多个众数。如果我们有一组数据集:
  
  1, 2, 3, 3, 3, 4, 5, 6, 6, 6, 7, 8, 9
  
  其中有两个众数 3 和 6，因为这两个值都出现了三次，出现频率最高，而其他的值都只出现了一次。

随机变量

随机变量
- 是某些进程（很多时候……“某些进程”意义比较模糊）的可能值的占位符。如前所述，符号能帮我们简化复杂的意义（通常是单个字母或单个字符）。我们看到随机变量用大写字母表示（X、Y 或 Z 是表示随机变量的常用方法）。
- 我们可能有随机变量 X，它是某人在网站上所花费时间的可能值的占位符。或者随机变量 Y，它是某个人是否购买产品的可能值的占位符。
- X 是某人在我们网站花费时间的可能值的'占位符'，它可以是从 0 到无限的任意值。
大小写
- 随机变量用大写字母表示。每当我们观察到这些随机变量的一个结果，就用相同字母的小写表示。

符号表达式

聚合
- 聚合是一种将多个数字转换为较少数字（通常为一个数字）的方法。
求和
- 求和是一种常见的聚合方式。用于对值求和的符号是一个希腊字母符号，称为SigmaΣ。

均值
- 在均值计算的最后一步，我们引入 n 作为我们数据集中值的总数。我们可以将它放在求和符号的顶部，也可以在计算均值时作为分母。

描述性统计学 - 第二部分

离散程度测量

离散程度测量用于告诉我们数据之间的分散程度。常见的离散程度测量包括:
- 极差
- 四分位差 (IQR)
- 标准差
- 方差

直方图

直方图对于了解数值数据的不同方面是非常有用的。在后面的概念中，你将看到直方图的广泛使用，帮助你理解我们前面提到的关于数值变量的四个方面:
- 集中趋势
- 离散程度
- 形状
- 异常值

计算五数概括法中的值

五数概括法包括 5 个值：
- 最小值： 数据集中的最小值。
- Q1（第一四分位数）：排序后数据第 25% 处的值。
- Q2（中位数）：排序后数据第 50% 处的值。
- Q3（第三四分位数）：排序后数据第 75% 处的值。
- 最大值： 数据集中的最大值。

极差

极差又称全距，是最大值和最小值之间的差值。

四分位差

四分位差为Q3 和 Q1 之间的差值。

标准差与方差

标准差是最常见的数据离散程度度量之一。它的定义为每个观察值与均值之间的平均差异。
方差

方差是每个观察值与均值之差的平方值的平均数。标准差是方差的平方根。因此，标准差的计算如下所示:

总结

方差用于比较两组不同数据的离散程度。方差较高的一组数据相比方差较低的一组数据，其分布更为广泛。但是注意，有可能只有一个（或多个）异常值提高了方差，而大多数数据实际上比较集中。
在比较两个数据集之间的离散程度时，每个数据集的单位必须相同。
当数据与货币或经济有关时，方差（或标准差）更高则表示风险越高。
在实践中，标准差比方差更常用，因为它使用原始数据集的单位。

形状

从直方图中，我们可以快速识别数据的形状，这会影响我们在之前概念中学到的所有度量。我们学了数据的分布通常为以下三种形状之一：

1. 右偏态

2. 左偏态

3. 对称分布（通常是正态分布）

形状	均值与中位数	现实世界中的应用
对称（正态）	均值等于中位数	身高、体重、误差、降雨量
右偏态	均值大于中位数	血液中残留的药物量，呼叫中心的电话间隔时间，灯泡多久熄灭
左偏态	均值小于中位数	许多大学的成绩百分比，死亡年龄，资产价格变动

异常值

我们了解到异常值是明显偏离我们其余数据点的点。这会极大地影响均值和标准差等度量，而对五数概括法中的第1四分位数、中位数、第2四分位数的影响较小。
识别异常值
- 有许多不同的技术用于识别异常值。这里提供了有关此话题的一篇完整论文。

处理异常值常用技术

当出现异常值时，我们应该考虑以下几点。

1. 注意到它们的存在以及对概括性度量的影响。

2. 如果有拼写错误 —— 删除或改正。

3. 了解它们为什么会存在，以及对我们要回答的关于异常值的问题的影响。

4. 当有异常值时，报告五数概括法的值通常能比均值和标准差等度量更好地体现异常值的存在。

5. 报告时要小心。知道如何提出正确的问题。

异常值处理建议

绘制你的数据以确定是否有异常值。

2. 通过上述方法处理异常值。

3. 如果无异常值，且你的数据遵循正态分布，使用均值和标准差来描述你的数据集，并报告数据为正态分布。

描述统计与推论统计

描述统计是用来描述收集的数据。
推论统计在于使用我们收集的数据对更大的总体数据得出结论。
- 总体 —— 我们想要研究的整个群体。
- 参数 —— 描述总体的数值摘要
- 样本 —— 总体的子集
- 统计量 —— 描述样本的数值摘要

录取案例分析——辛普森悖论

用不同方式对数据进行分组，会让结论消失甚至相反

概率

掷硬币的结果可以为 T 或 H ，分别作为硬币的反面和正面。
然后基本规则为真：
1. P(H)=0.5
2. 1 - P(H) = P(not H)=0.5 其中 not H 是除了正面以外的事件。既然只会出现两种可能的结果，我们得到 P(not H)=P(T)=0.5。
3. 通过多次掷硬币，我们得到 n 次正面的概率为
  
  因为这些事件是独立的。
我们从中得到下面两个通用规则：
1. 任何事件的概率在 0 和 1 之间，其中包括 0 和 1。
2. 互补事件的概率为 1 减去某个事件的概率。其他一切可能事件的概率是 1 减去某个事件本身的概率。因此所有可能事件概率的总和等于 1。
3. 如果我们事件是独立的，一系列可能事件的概率是这些事件的乘积。某个事件的概率 AND 下一个事件的概率 AND 下一个事件的概率，即这些事件概率的乘积。

二项分布

二项分布 帮助我们决定一系列独立的 '掷硬币等事件' 概率。

与二项分布相关的概率质量函数具有以下形式：

其中 n 是事件数量， x 是 "成功" 的数量，p 是 "成功" 的概率。

我们现在可以使用这个分布决定下列事件的概率：
- 掷硬币 10 次出现 3 次正面的概率。
- 掷硬币 10 次出现 8 次以上正面的概率。
- 掷硬币 20 次不出现正面的概率。

条件概率

条件概率，通常事件并不像掷硬币和骰子一样是独立的。实际上，某个事件的结果依赖于之前的事件。
例如，得到阳性检验测试结果的概率依赖于你是否具有某种特殊条件。如果具备条件，测试结果就是阳性的。我们通过以下方式用公式表示任意两个事件的条件概率：

在这个例子中，我们得到下列内容：

其中 |代表 "鉴于"，∩ 代表 "和".

贝叶斯规则

P(A|B)已知B发生后A的条件概率（A的后验概率）
P(A)是A的先验概率（边缘概率）
P(B|A)已知A发生后A的条件概率（B的后验概率）
P(B)是B的先验概率（边缘概率）

模拟掷硬币

#公平硬币
import numpy as np
np.random.randit(0 , 2, size=1000)#0:默认下限；2：默认上限（但不包括上限本身），模拟掷硬币1000次
#非公平硬币
np.random.choice([0, 1], size=1000, p=[0.8, 0.2])#p:给定0， 1发生概率
np.random.choice(pop_data, size=(10000, 3))#从pop_data中进行3次取样，循环10000次试验

#注：若不给定P，则返回0， 1概率相等

正态分布

import numpy as np
np.random.binomial(n, p, size)#n:事件数量（如一次抽10枚硬币），P：概率， size:试验次数

抽样分布与中心极限定理

抽样分布

抽样分布 是样本的分布。

抽样分布符号法

首先我们将 抽样分布 定义为 样本量的分布。
抽样分布以初始参数值为中心。
根据样本容量大小，抽样分布降低了方差。具体说来，抽样分布的方差等于初始数据除以样本容量的方差。这也同样适用于样本平均数方差！

参数与统计的符号法

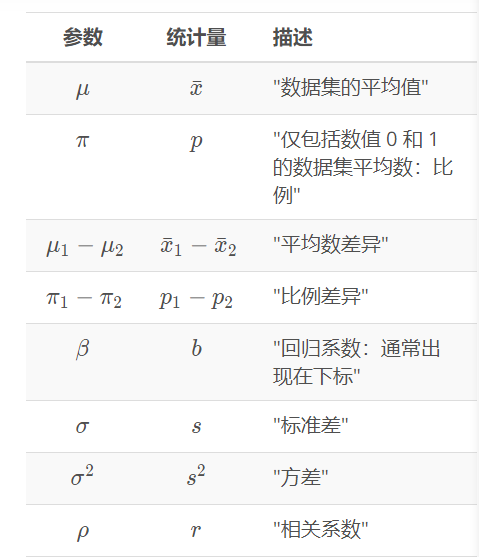
抽样分布涉及的两个重要数学定理包括：
1. 大数法则
2. 中心极限定理
大数法则 表示 随着样本容量增加，样本平均数越来越接近总体平均数
下面是三种最常见的估计技巧：
中心极限定理 表示 样本容量足够大，平均数的抽样分布越接近正态分布。

中心极限定理 实际上应用于这些常见的统计量中：
1. 样本平均数 (x¯)
2. 样本比例 (pp)
3. 样本平均数的差异 (x¯1−x¯2)
4. 样本比例的差异 (p1−p2)*
自助法 (bootstrap) 是放回抽样。在 python 中使用 random.choice 实际上是自助法。无论选择多少次，我们数据集中任何数字的概率保持不变。抛硬币和掷骰子也是自展抽样，因为在一个场景中滚动出 6，并不意味着后面出现 6 的概率降低。

总结

抽样分布
- 抽样分布 是一个统计量 (任何统计量) 的分布。
  - 抽样分布涉及两个重要数学定理：大数法则 和 中心极限定理。
  - 大数法则 表示随着样本容量增加，样本平均数越来越接近总体平均数。一般来说，如果统计量 "较好地" 估计参数，它会接近较大样本容量的参数。
  - 中心极限定理 表示样本容量足够大，样本平均数会是正态分布，但是在多个样本平均数情况下，它才为真。
- 自展法
  - 自展法 是我们从群组中进行放回抽样的技巧。
  - 我们可以使用自展法，模拟在这节课进行多次的创建抽样分布。
  - 通过自展法，计算我们统计量的重复数值，我们可以理解统计中的抽样分布。

置信区间

我们可以使用自助法和抽样分布，构建感兴趣参数的置信区间。

通过找出对感兴趣参数进行最好估计的统计量 (例如样本平均数估算总体平均数或样本平均数的差异估算总体平均数的差异)，我们可以很容易构建感兴趣参数的置信区间。
你可以将置信区间理解为 可信度为 95% ，总体平均数落在你发现的范围内 。注意根据构建置信区间的目的和每端删除的百分比，百分比和参数都会发生变化。
现实意义应为实际显著性——Practical significance；统计意义应为统计显著性——statistical significance
使用置信区间和假设检验，你能够在做决策时提供 统计显著性。

然而，做决策时考虑 实际显著性 同样很重要。 实际显著性 考虑到所处情况的其他因素，假设检验或置信空间的结果可能不会直接考虑到这种情况。空间、时间或金钱等约束条件对商业决定很重要。但是可能不会在统计测试中直接考虑这些因素。

置信区间的其他相关语言

了解样本容量和置信度与最终分析后置信区间的关系，这是非常重要的。

假设你可以控制分析中其他所有条目：
1. 增加样本容量，会降低置信区间的宽度。
2. 增加置信度 (如 95% 增加到 99%) 会增加置信区间的宽度。
你注意到可以计算：
1. 置信区间宽度，作为置信区间上限与下限的差异。
2. 误差范围 是置信区间宽度的一半，通过对样本估计值的加减，达到置信区间的最终结果。

假设检验

设置假设检验

在收集数据前，H0 为真。
H0 通常表示没有影响或对两组影响相同。
H0 和 H1 是竞争性、非重叠的假设。
H1 可以证明为真。
H0 包含一个等号：= 、q≤ 或 q≥。
H1 包含非空值：q≠、>> 或 <<。

H0: 无辜的

H1: 有罪的

我们可以认为在收集数据之前，"无辜的" 为真。然后备择假设必须是竞争性、非重叠的假设。因此备择假设为一个人有罪。
- 我们想测试新页面是否优于已有页面，我们设置备择假设。两个指标需要遵守，一是零假设应当包含等于号，二是备择假设应当包含我们希望为真的陈述。因此，它应为以下形式：
  
  H0:μ1≤μ2
  
  H1:μ1>μ2
  
  这里，μ1 代表新页面返回的总体平均数。同样，μ2 代表原来页面返回的总体平均数。

错误类型

I 类错误 包含以下特征：
1. 你应该设置零假设和备择假设，I 类错误是更严重的错误。
2. 它们由 α 符号表示。
3. I 类错误的定义是： (H0) 为真时，认为备择假设 (H1) 为真。
4. I 类错误通常称为误报。
II类错误
1. 它们由 \betaβ 符号表示。
2. II 类错误的定义是：(H1) 为真时，认为零假设 (H0) 为真。
3. II 类错误通常称为漏报。

常见的假设检验包括：

测试总体平均数 (单样本 t 检验)。
测试均数差 (双样本 t 检验)
测试个体治疗前后的差异 (配对 t 检验)
测试总体比例 (单样本 z 检验)
测试总体比例的差异 (双样本 z 检验)

P值

p 值的定义是 如果零假设为真，观察到统计量 (或支持备择假设的更多极端) 的概率。

联通错误和P值

p 值是零假设为真时，得到统计量或更极端数值的概率。
- 所以，p 值小，表示零假设不正确。相反，我们的统计量可能来自不同于零假设的分布。
- p 值很大时，我们可以证明统计量很可能来自零假设。所以我们无法证明拒绝零假设。
- 通过对比 p 值和 I 类错误阈值 (\alphaα)，我们可以决定选择哪个假设。
pval≤α⇒ 拒绝 H0

pval>α⇒ 不拒绝 H0

弗朗尼校正法

如果完成多个假设检验，你的 I 类错误更加严重。为了纠正这点，通常采用 邦弗朗尼 校正法。这种校正法 非常保守，但是假如 I 类最新错误率应为实际想得到的错误率除以完成检验的数量。
所以，如果你想在 20 个假设检验中把 I 类错误率维持在 1%，邦弗朗尼 校正率应为 0.01/20 = 0.0005。你应该使用这个新比率，对比每 20 个检验的 p 值，做出决定。

总结

无论是在零假设还是在备择假设中，陈述时要避免出现接受这个单词。我们并不是陈述某个假设为真。相反对于 I 类错误的阈值，你根据零假设中数据的相似性做出决定。
所以，可以出现在假设检验中的措辞包括：我们拒绝零假设 或者 我们不拒绝零假设。这有助于你最初零假设默认为真，并且如果没有收集数据，在测试最后 "选择" 零假设，是正确选择。
如何设置假设检验。学习了零假设是收集数据前我们假设正确的内容，备择假设是我们想要证明为真的内容。
I 类错误和 II 类错误。I 类错误是最严重的错误类型，这与零假设实际为真时选择备择假设相关。
p 值是零假设为真的情况下，观察支持备择假设的数据或更极端内容的概率。利用拔靴样本得到的置信区间，可以做出与假设检验相同的决定 (在没有混淆 p 值的情况下)。
如何根据 p 值做出决定。如果 p 值小于 I 类错误阈值，你可以拒绝零假设，选择备择假设。否则，不拒绝零假设。
样本容量很大时，任何内容都具有统计意义 (最终拒绝所有零假设)，但这些聚过不具有现实意义。
完成多个假设检验时，错误会更加严重。因此使用一些校正法，确保 I 类错误率，非常重要。邦弗朗尼校正是简单且保守的一种方法，你应该用 α 水平 (或 I 类错误阈值) 除以完成检验的数量。

回归

回归是常用的一种数据分析的方法，通过规定因变量和自变量来确定变量之间的因果关系，是一种建立回归模型，并根据实测数据来求解模型的各个参数，然后评价回归模型是否能够很好的拟合实测数据。学习回归分析，可以帮助我们对数据做出合理的预测。

机器学习简介

机器学习 通常分为监督和 非监督 学习，而你将在本课（接下来的课程还会涉及相关扩展知识）学到的回归则是监督机器学习的范例之一。
- 在监督机器学习中，你要做的是预测数据标签。一般你可能会想预测交易是否欺诈、愿意购买产品的顾客或某一地区的房价。
- 在非监督机器学习中，你要做的是收集同一类尚无标签的数据。
在简单线性回归中，我们要对两个定量变量进行比较。
- 反应变量是你想预测的变量，解释变量则是用于预测反应变量的变量，在线性回归中，通常我们会用散点图来可视化两个变量的关系

散点图

散点图是比较两个定量变量的常用可视化手段。散点图常用的汇总统计是 相关系数，该系数常以 r 来表示。
虽然还有其它几种办法来衡量两个变量之间的相关性，但最常用的办法是用皮尔逊相关系数，该系数能说明 线性关系 的：
1. 相关程度
2. 相关方向
斯皮尔曼相关性系数则不只衡量线性关系，可能更适用于关联两个变量的场合。

回归线决定因素

回归线通常由截距和斜率决定。
- 截距的定义为 当 x 变量为 0 时，反应变量的预测值。
- 斜率的定义为 x 变量每增加一个单位引起的反应变量的预测变化。
我们将线性回归的回归线记为：

y^=b0+b1x1
- 其中
  
  y^ 为回归线反应变量的预测值。
  
  b0 为截距。
  
  b1 为斜率。
  
  x1 为解释变量。

拟合回归线

要找出最佳回归线，我们用的主要算法叫做 最小二乘法，使用该算法，我们可找出一条最小化

的回归线。

决定系数

*决定系数即相关系数的平方。

决定系数变量通常定义为模型中能以 x 变量解释的反应变量的变化范围。通常来说，决定系数越接近 1，模型就越拟合数据。

多元线性回归

统计学习简介

虚拟变量

要往线性模型里添加分类变量，就需要把分类变量转变为 虚拟变量。
转化后，你需要舍弃一个 虚拟列，才能得到满秩矩阵。
如果你要用 0 、1 编码来创建虚拟变量，你就得舍弃一个虚拟列，确保所得矩阵是满秩的（这样你从 python 里得到的解才会是可靠的。）

逻辑回归

Project : A / B 测试

data_analysis_projects

注：学习笔记是在优达学城学习时，参考部分课程内容总结而成。

Project:分析 A / B 测试结果-项目心得：
项目描述：通过项目对网页 A / B测试有了初步认识，对于网站利用A / B test来测试新网站是否推出等问题有了新的理解。用Python以及Pandas包、Numpy包、statsmodels包、matplotlib包等分析某电子商务网站运行 A / B 测试的结果，并给出该公司建议：是否应该使用新的页面，保留旧的页面，或者应该将测试时间延长，之后再做出决定。
项目收获：熟悉A / B 测试流程，熟悉A / B流程中的统计方法，进一步学习了如何进行数据分析，加强了对理论联系实际的认知。

学习资源

Python 编程

Intro to Computer Science 学习if 语句，循环，函数，列表，集合和字典。
Programming Foundations with Python学习Python中的类，对象，模块。
NumPy and Pandas by Udacity 学习 NumPy 和 Pandas。
Python for Data Analysis 是最好的学习 NumPy, pandas, Matplotlib 的资源之一。它由这几个库的创始人 Wes McKinney 所撰写，这是使用这些库的详尽指南。

数据分析学习笔记part_4

数据分析

Lesson 4 : 统计学

描述性统计学 - 第一部分

数据类型

定序和定类

连续和离散数据

总结

集中趋势测量

众数（mode）

随机变量

符号表达式

描述性统计学 - 第二部分

离散程度测量

直方图

计算五数概括法中的值

极差

四分位差

标准差与方差

总结

形状

异常值

处理异常值常用技术

描述统计与推论统计

录取案例分析——辛普森悖论

概率

二项分布

条件概率

贝叶斯规则

正态分布

抽样分布与中心极限定理

抽样分布

抽样分布符号法

参数与统计的符号法

总结

抽样分布

置信区间

置信区间的其他相关语言

假设检验

设置假设检验

错误类型

常见的假设检验包括：

P值

联通错误和P值

弗朗尼校正法

总结

回归

机器学习简介

散点图

相关系数

回归线决定因素

拟合回归线

决定系数

多元线性回归

虚拟变量

逻辑回归

Project : A / B 测试

学习资源

Python 编程

猜你喜欢