本blog主要介绍了二叉堆、二项式堆,下一篇博客将介绍斐波拉契堆。
二叉堆和二项式堆、斐波拉契堆都是用于实现优先队列的高级数据结构,以不同堆实现的优先队列会有不同的时间复杂度。
问题引入
在实际应用中,我们经常会遇到在最多由n个数组成的动态集合 上得到这个集合里面的最大值或者最小值。这里的动态是指:集合S里面的元素可能会随时增加、删除、修改、返回最小值、返回最小值并删除一个最小值。
我们把用于解决此类的问题的抽象数据结构定义为优先队列:priority queue.之所以叫优先队列是指里面的元素都是具有偏序关系的、也就是可以比较大小的。
priority_queue有以下几种基本操作:
- insert(H,x) 插入一个值域为x的元素
- makeheap()建立一个新的堆H
- extractmin(H)返回优先队列H的最小值,同时将这个最小值从优先队列中删除。
- decreasekey(H,x,k)把H中的某个值域为x的元素的值改成k
- union(H1,H2):把H1和H2中的所有元素提取出来形成一个新的优先队列。
优先队列的基础数据结构可以是链表、二叉堆、二项式堆、斐波拉契堆,
基于不同的基础数据结构,优先队列的各个操作的时间复杂度的关系是:
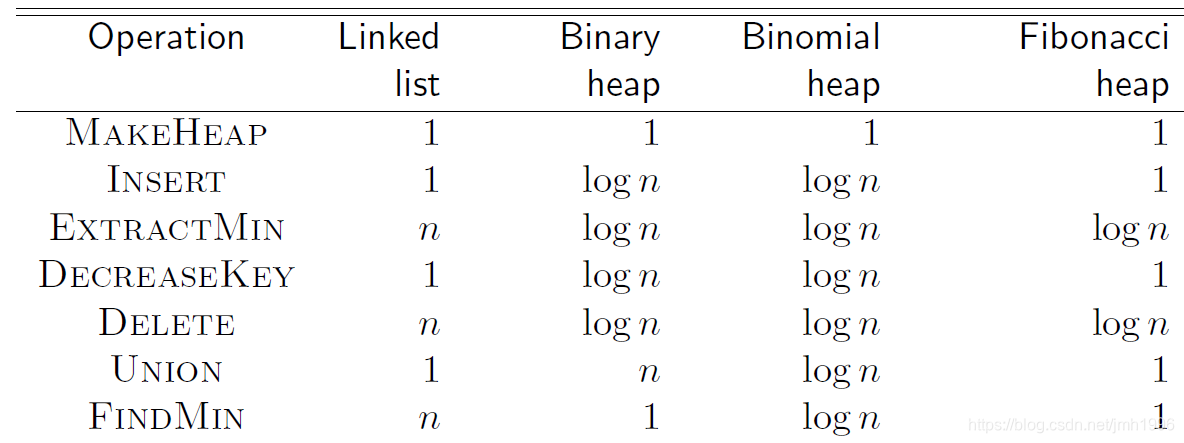
可以看到基于链表的优先队列的性能最差,二叉堆、二项式堆、斐波拉契堆的性能依次优化。
基于链表的优先队列
我们可以使用链表或者数组这种数据结构来实现优先队列,我们假设选择的是数组。
假设数组里面的元素是有序的。
这种情况下,makeheap就是只要申请一个数组即可,时间复杂度为O(1)
insert 需要将元素插入合适的位置,选择合适的位置使用二分查询需要
时间,但是合适位置只有的元素都要向后移,时间复杂度为
extractmin取最小元素需要O(1),删除这个最小元素需要把后面的元素往前移动一个位置。
decreasekey修改某个元素的值。O(1)
delete删除需要O(n)
union也是需要O(n)
findmin只需要O(1)
假设数组里面的元素是无序的。
这种情况下,makeheap就是只要申请一个数组即可,时间复杂度为O(1)
insert 需要将元素插入到末尾,O(1)
extractmin取最小元素需要遍历整个数组,并将这个元素删除,需要O(n)
decreasekey修改某个元素的值。O(1)
delete删除需要O(n)
union也是需要O(n)
findmin只需要O(n)
因此使用数组的话,无论是否对数组进行排序,所需要性能都不是很好。
这是因为,我们让这个数组全部元素都有序实在太严格,甚至是有些浪费了。我们只是想知道最小的元素,但是是在是没有必要让整个数组有序。如果有某种方式,使得我们不用所有元素都有序也得得到当前最小值,那就好啦。
而这个就是二叉堆的核心思想:我们用树来存储所有的元素,然后我们让树的根比它的子节点的值都小就好啦。
基于二叉堆的优先队列
二叉堆是一个完全的二叉树,这种树里面的各个节点有指针域和值域。指针域放着指向其父节点、左右孩子的指针。值域放着数据对象T ,必须定义这些对象的偏序关系。即 必须使得二元关系
是有定义的。二叉堆对发在各个节点的数据对象有一个很弱的要求:父节点的数据对象必须小于等于(或者大于等于)其子节点的数据对象。若一个堆的父节点的数据对象小于等于(或者大于等于)其子节点的数据对象,这就是一个小顶堆。如果父节点的数据对象大于等于其子节点的数据对象,那么这就是一个大顶堆。
大小顶堆的原理一样,以下只介绍小顶堆。
以下是一些小顶堆:
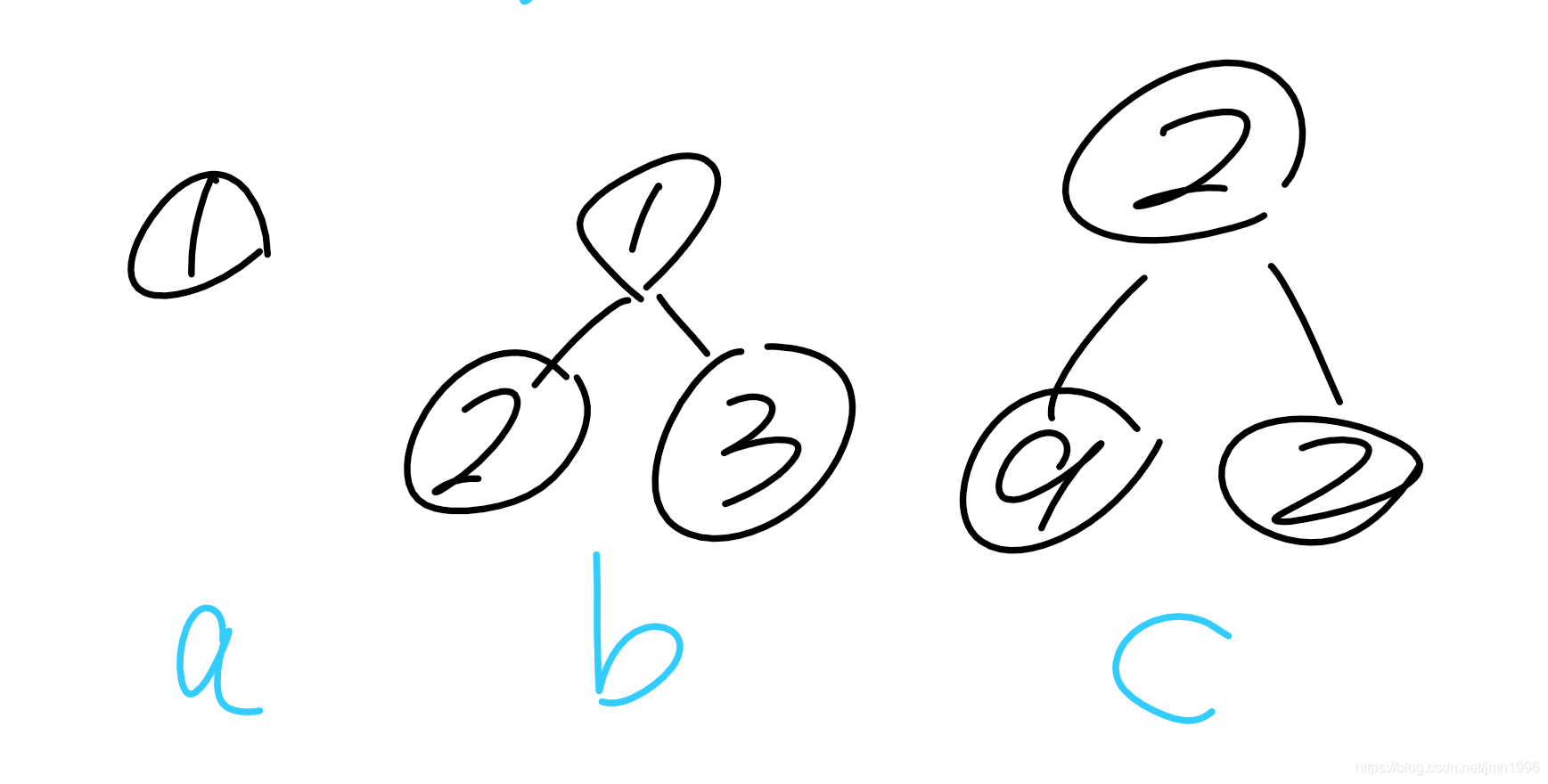
现在,我们使用一个二叉堆来实现优先队列。
既然要实现优先队列,那么就需要实现以下函数:
- MakeHeap_VOID() 建立一个空的堆
- MakeHeap([x1,x2,…]) 给定一组数据对象xi,基于这些元素建立堆
- INSERT(x) 把数据对象插入到堆里面
- FINDMIN() 返回堆的最小值
- EXTRACTMIN() 返回最小值,并把堆顶的元素删除
- UNION() 把两个堆的元素合并起来形成一个新的堆。
OK,我们一个个来看看这些函数如何实现。
INSERT(x)函数
对于一个新的元素x,我们要把这个x插入到堆里面。那么我们的做法只需要
1.把x插到堆的末尾。注意一定要是末尾,如果不是末尾,这个堆对应的树就不是满二叉树了。
2.从刚刚插入的这个节点开始,从叶子节点往根节点更新。如果这个插入的值比父节点还小,那么这个刚刚插入的值就是以其父节点为根的子树的最小值,此时需要把这个节点的值与父节点的值交换。一直往上找,直到父节点比这个新插入的元素小位置或者到达根节点。
时间复杂度:最坏的情况下,这个新元素就是所有元素中的最小值。此时,从叶子到根遍历了logn个节点。
所以复杂度是O(logn)
FINDMIN()返回最小值
堆的根节点的元素就是当前最小值。
EXRACTMIN()返回最小值,同时将最小值删除
得到最小值就只需要当前的堆顶,先把这个堆顶的值保存。
然后将堆顶删除掉。
删除的方法是:
把堆的最后一个元素的值放到堆顶,删除最后一个元素。然后从堆顶开始,从上往下的维护堆。
时间复杂度:O(logn)
DECREASEKEY(ptr,value)把指针ptr指向的节点的值改成value.
这个问题分两种情况来看。
1.把ptr对应的节点的数据改小。
这种情况下,ptr对应的节点依然会小于其子节点。所以无需向下维护。
但是ptr节点的新值有可能小于父节点的值,所以需要从ptr向上的维护堆序。
例如:
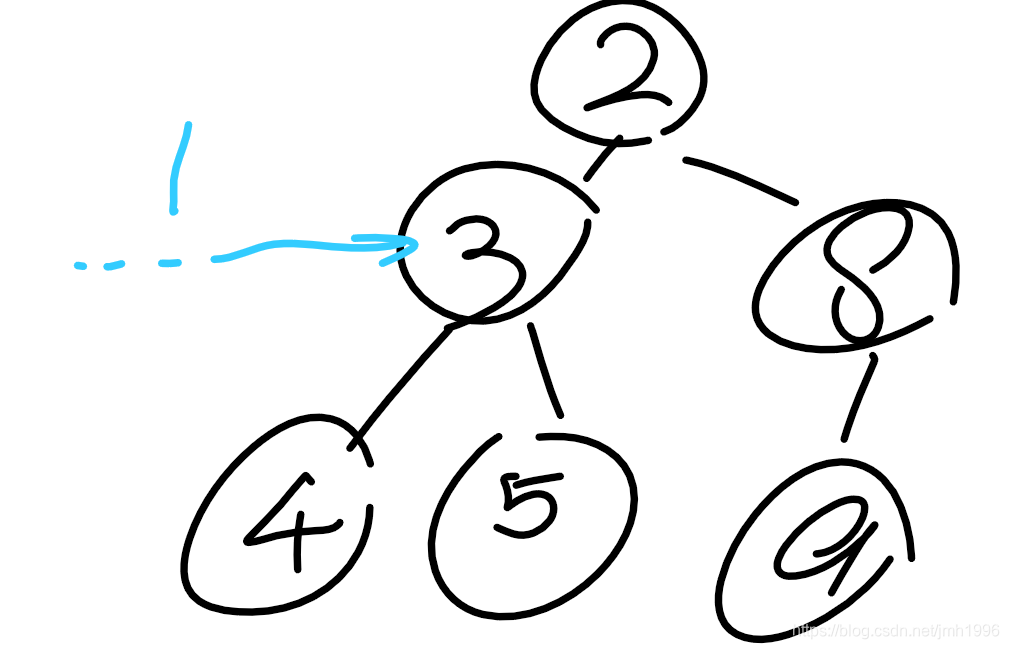
2.把ptr对应的节点的数据改大。
这种情况下,父节点依然小于这个节点,于是该节点向上的部分可以不用去考虑。
但是该节点被改大以后,就不一定比其子节点都小。此时需要从这个节点开始递归的向下维护。单次维护的方式很简单,就是与其最小的那个子节点交换。然后交换后,从刚刚交换的子节点递归的向下维护。
例如:

MakeHeap_LIST()从一堆数据中建堆
从给定的一批数据建立起堆。
有两种方法。
1.对于每一个元素,调用insert函数,将这个元素插入。
时间复杂度O(nlogn),这是因为一共有n个元素待插入,每次插入需要logn复杂度。
所以总的时间是:
2.先把所有的元素都拷贝到这个堆里面。当时这个堆肯定是不满足要求的,这个时候,我们从最后一个非叶子的子树开始,从后往前一个个小子树的维护堆序,每个小子树是从上往下的维护。
此时的复杂度为O(n)
这是因为:
对于第k层节点来说,一共有
个节点,每个节点为根的子树从上向下维护最多需要logn-k步。
所以总的时间复杂度为:
这个式子是怎么推的呢?
记
,那么
可以写成:
前一部分是个等比数列求和,后一个是一个错位相减法求和。
记
那么:
两边同乘以2
于是有:
容易得到
所以:
而
所以
UNION()将两个二叉堆合并
实际中是由将两个优先队列的元素合并在一起的需求的。
在二叉堆中,如果要将两个堆合并,有两种方法:
1.将两个堆的元素全部放在一块,然后对这些元素调用MAKEHEAP_LIST方法,在O(n)的时间内合并。
2.遍历其中一个堆的每个元素,将调用INSERT函数把这些元素插入到另外一个堆里面,需要O(nlogn)的时间。
**可以看到:二叉堆对于合并操作的支持为O(n),这个是很慢的!所以,人们提出了二项式堆来加速这个合并操作。**这个下一篇博客介绍。
基于二叉堆的优先队列实现
以下是一个基于二叉堆的优先队列的实现
#pragma once
#include <vector>
#include <algorithm>
using namespace std;
template <typename T>
class binaryHeap
//基于数组,建立一个二项堆
{
public:
binaryHeap()
{
MakeHeap();
}
void MakeHeap()
{
min_heap.clear();
min_heap.push_back(T());//min_heap[0]是无效的
theLast = 1;
}
void MakeHeap2()
{
//从下往上修正,从倒数第二层开始
int end_s = (theLast-1) / 2;
while (end_s>0)
{
int lchild = end_s * 2;
int rchild = end_s * 2 + 1;
int select_node = 0;
if (lchild < theLast && rchild < theLast)
//有两个子节点
{
if (min_heap[lchild] < min_heap[rchild])
{
select_node = lchild;
}
else
{
select_node = rchild;
}
}
else if (lchild < theLast)
//只有左节点
{
if (min_heap[lchild] < min_heap[end_s])
//需要交换
{
select_node = lchild;
}
}
else if (rchild < theLast)
//只有右节点
{
if (min_heap[rchild] < min_heap[end_s])
{
select_node = rchild;
}
}
else
//没有叶子节点
{
}
if (select_node && min_heap[select_node] < min_heap[end_s])
//子节点的最小大于父节点,进行维护
{
T tmp = min_heap[select_node];
min_heap[select_node] = min_heap[end_s];
min_heap[end_s] = tmp;
//因为一个更大的父节点的值换到select_node这个子节点了,所以要把select_node为根的树重新维护一下堆的序
maintain_order(select_node);
}
end_s--;
}
}
binaryHeap(T * A, int n)
//从一个T类型的数组中建立一个堆
{
MakeHeap();
for (int i = 0; i < n; i++)
//无脑的先拷贝过来,然后一个个的维护这样子实现的复杂度为O(n)
{
min_heap.push_back(A[i]);
theLast++;
}
MakeHeap2();
}
void DECREASEKEY(int node, T value)
//把某个位置node上的值改成 value
{
if (value < min_heap[node])
//往小的改,那么只需要向上维护
{
min_heap[node] = value;
maintain_order2(node);
}
else if (value>min_heap[node])
//往大的改,那么需要向下维护
{
min_heap[node] = value;
maintain_order(node);
}
}
void INSERT(T x)
//从低部向上
{
min_heap.push_back(x);
theLast++;
maintain_order2(theLast);
}
T FINDMIN()
{
return min_heap[1];
}
T EXTRACTMIN()
{
T rst = min_heap[1];
min_heap[1] = min_heap[theLast-1];
theLast--;
maintain_order(1);
return rst;
}
void UNION(binaryHeap &rhs)
//合并直接把rhs的所有元素都直接附在后面,然后调用MakeHeap2()维护新的堆
//时间复杂度为O(n+2n)-->O(n)
{
for (int i = 1; i <= rhs.theLast; i++)
{
min_heap.push_back(rhs[i]);
theLast++;
}
MakeHeap2();
}
~binaryHeap()
{
}
private:
void maintain_order2(int child)
//给定某个节点,向上维护
{
int end_s = child;
while (end_s>0)
{
int parent = end_s / 2;
if (min_heap[end_s] < min_heap[parent])
{
T tmp = min_heap[end_s];
min_heap[end_s] = min_heap[parent];
min_heap[parent] = tmp;
end_s = parent;
}
else
//无需再维护
{
break;
}
}
}
void maintain_order(int root)
//给定根root,从顶向下维护以root为根的子树的序
{
int lchild = root * 2;
int rchild = root * 2 + 1;
int select_node = 0;
if (lchild < theLast && rchild< theLast)
{
if (min_heap[lchild] < min_heap[rchild])
{
select_node = lchild;
}
else
{
select_node = rchild;
}
}
else if (lchild<theLast)
{
select_node = lchild;
}
else if (rchild<theLast)
{
select_node = rchild;
}
if (select_node && min_heap[select_node] < min_heap[root])
{
T tmp = min_heap[root];
min_heap[root] = min_heap[select_node];
min_heap[select_node] = tmp;
maintain_order(select_node);
}
else
{
return;
}
}
private:
vector< T > min_heap;
int theLast;
};