参数化算法(Cyrus-Beck)

考虑凸多边形区域R和直线段P1P2：P(t)=(P2-P1)*t+P1
设A是区域R的边界上一点，N是区域边界在A点的内法线向量

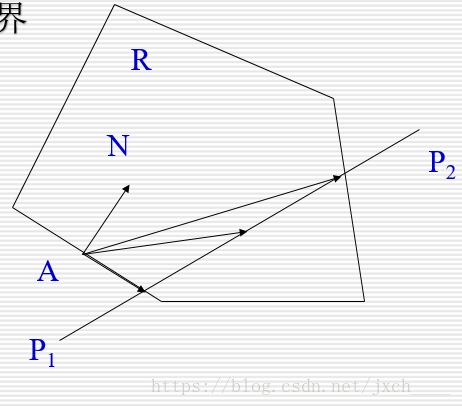
则对于线段P1P2上任一点P(t)
N ·(P(t)-A)< 0 $\to$ 外侧
N ·(P(t)-A)>0 $\to$ 内侧
N ·(P(t)-A)=0 $\to$ 边界或其延长线上
凸多边形的性质：点P(t)在凸多边形内的充要条件是，对于凸多边形边界上任意一点A和该点处内法向N，都有N·(P(t)-A)>0

k条边的多边形，可见线段参数区间的解:
Ni· (p(t)-Ai)>=0, i=0,…,k, 0≤t ≤1.
即：Ni· (P1-Ai)+ Ni· (P2-P1) t>=0

令ti= Ni· (P1-Ai)/[Ni· (P2-P1) ]
Ni· (P2-P1) =0-> 平行于对应边。
此时判断Ni· (P1-Ai)
若Ni· (P1-Ai) <0 $\to$ P1 P2在多边形外侧->不可见，
若Ni· (P1-Ai) >0 $\to$ P1 P2在多边形内侧->继续其它边的判断
对于t值的选择：首先，要符合0≤t≤1；其次，对于凸窗口来说，每一个线段与其至多有两个交点，即有两个相应的t值。所以我们可以把计算出的t值分成两组：一组为下限组，是分布在线段起点一侧的；一组为上限组，是分布在线段终点一侧的。这样，只要找出下限组中的最大值及上限组中的最小值，就可确定线段了。
分组的依据是：
如果Ni· (P2-P1) ＜0，则计算出的值属于上限组
如果Ni· (P2-P1) ＞0，则计算出的值属于下限组

参数化算法的几何意义

上限组以Ni· (P2-P1) <0为特征，表示在该处沿P1P2方向前进将越来越远地离开多边形区域。
下限组以Ni· (P2-P1) >0为特征，表示在该处沿P1P2方向前进将接近或进入多边形内侧。

因此，线段可见的交点参数：
tl=max{0,max{ti: Ni· (P2-P1) >0}}
tu=min{1,min{ti: Ni· (P2-P1)<0}}
若 tl <= tu, [tl ， tu]是可见线段的交点参数区间，否则，线段不可见。

当凸多边形是矩形窗口且矩形的边与坐标轴平行时，该算法退化为Liang-Barsky算法。