一、题目:最长公共子序列:
给定两个字符串,求解这两个字符串的最长公共子序列(Longest Common Sequence)。比如字符串L:BDCABA;字符串S:ABCBDAB
则这两个字符串的最长公共子序列长度为4,最长公共子序列是:BCBA
思路:动态规划:时间O(n * m),空间O(n * m)
创建 DP数组C[i][j]:表示子字符串L【:i】和子字符串S【:j】的最长公共子序列个数。
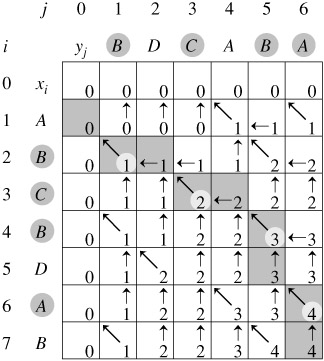
状态方程: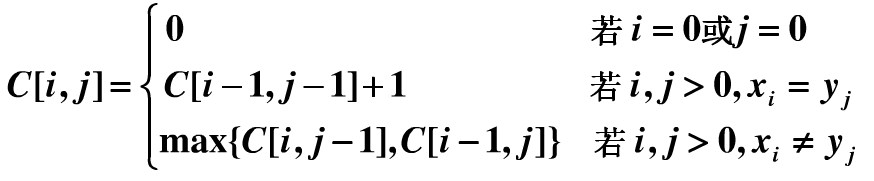
个数代码:
def LCS(L,S): if not L or not S: return "" dp = [[0] * (len(L)+1) for i in range(len(S)+1)] for i in range(len(S)+1): for j in range(len(L)+1): if i == 0 or j == 0: dp[i][j] = 0 else: if L[j-1] == S[i-1]: dp[i][j] = dp[i-1][j-1] + 1 else: dp[i][j] = max(dp[i-1][j],dp[i][j-1]) return dp[-1][-1] L = 'BDCABA' S = 'ABCBDAB' LCS(L,S)
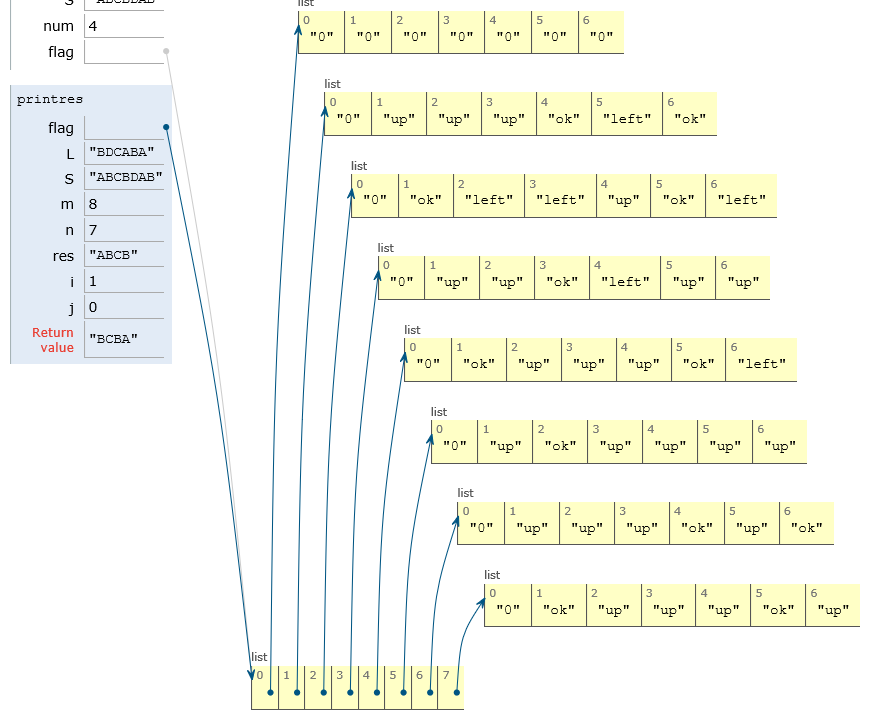
最长子序列代码:设置一个标志
def LCS(L,S): if not L or not S: return "" res = '' dp = [[0] * (len(L)+1) for i in range(len(S)+1)] flag = [['left'] * (len(L)+1) for i in range(len(S)+1)] for i in range(len(S)+1): for j in range(len(L)+1): if i == 0 or j == 0: dp[i][j] = 0 flag [i][j] = '0' else: if L[j-1] == S[i-1]: dp[i][j] = dp[i-1][j-1] + 1 flag[i][j] = 'ok' else: dp[i][j] = max(dp[i-1][j],dp[i][j-1]) flag[i][j] = 'up' if dp[i][j] == dp[i-1][j] else 'left' return dp[-1][-1],flag def printres(flag,L,S): m = len(flag) n = len(flag[0]) res = '' i , j = m-1 , n-1 while i > 0 and j > 0: if flag[i][j] == 'ok': res += L[j-1] i -= 1 j -= 1 elif flag[i][j] == 'left': j -= 1 elif flag[i][j] == 'up': i -= 1 return res[::-1] L = 'BDCABA' S = 'ABCBDAB' num,flag = LCS(L,S) res = printres(flag,L,S)
二、题目:最长递增子序列
给定一个长度为N的数组,找出一个最长的单调自增子序列(不一定连续,但是顺序不能乱)。例如:给定一个长度为6的数组A{5, 6, 7, 1, 2, 8},则其最长的单调递增子序列为{5,6,7,8},长度为4.
解法一:最长公共子序列:O(N^2)
这个问题可以转换为最长公共子序列问题。如例子中的数组A{5,6, 7, 1, 2, 8},则我们排序该数组得到数组A‘{1, 2, 5, 6, 7, 8},然后找出数组A和A’的最长公共子序列即可。显然这里最长公共子序列为{5, 6, 7, 8},也就是原数组A最长递增子序列。
解法二:动态规划法(时间复杂度O(N^2))
设 dp(j) 表示L中以 L[j] 为末元素的最长递增子序列的长度。状态方程:
dp(j) = { max(dp(i)) + 1, i<j且L[i]<L[j] }
这个递推方程的意思是,在求以L【j】为末元素的最长递增子序列时,找到所有序号在 j 前面且小于L【j】的元素L【i】,即 i < j 且 L【j】< L【i】。
例如给定的数组为{5,6,7,1,2,8},则 dp(0)=1, dp(1)=2, dp(2)=3, dp(3)=1, dp(4)=2, dp(5)=4。所以该数组最长递增子序列长度为4,序列为{5,6,7,8}。
代码:
def LCS1(L): if not L: return "" dp = [1] * len(L) for j in range(len(L)): for i in range(j):
#当j = 5,i = 0时,dp = [1,2,3,1,2,1]
#当j = 5,i = 0时,dp[5] = 1 < dp[0]+1,故dp(5)更新为dp[0]+1=2,
#当j = 5,i = 1时,dp[5] = 2 < dp[1]+1 =3,故dp(5)更新为dp[1]+1=3
#当j = 5,i = 2时,dp[5] = 4
#当j = 5,i = 3时,dp[5] = 4 > dp[3]+1 = 3,故dp[5]不更新,同理,i = 4时,dp[5]仍等于4 if L[j] > L[i] and dp[j] < dp[i] + 1:
dp[j] = dp[i]+1 return max(dp) L = [5,6,7,1,2,8] LCS1(L)
![]()
得到dp数组之后找出,最长递增子序列,
- 先找到dp最大值5,索引为7,然后arr【7】= 9
- dp【6】 = 5-1 =4,故arr【6】=8
- dp【4】 = 4-1或者dp【5】 = 4-1,故arr【4】 = 6 / arr【5】=4
- dp 【2】=3-1或者dp【3】 = 3-1,故arr【2】 = 5 / arr【3】=3
- 2 / 1
故最长递增子序列:2→5→6→8→9或者1→3→4→8→9