介绍

匈牙利算法用于解决求最大分配的分配问题，不等权重的二分图中求最大权分配的分配问题，使用KM算法。

本文首先介绍匈牙利算法所针对的二分问题

然后介绍匈牙利算法的原理

最后有匈牙利算法证明，证明为何使用该算法可以找到最大匹配

一个典型的分配问题是工作分配，假设有M份工作，总共有N个候选人，假设M小于等于N， $w_{mn}=1$ 表示候选人n胜任工作m，因此我们得到一个关联矩阵 $S\in \mathbb{R}^{m*n}$ ：

$\begin{bmatrix} 1 & 0 & 1\\ 1 & 1 &1 \\ 0 & 0 & 1 \end{bmatrix}$

对应的图G为

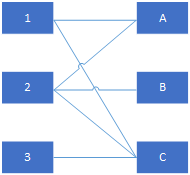
二分图

二分图定义

二分图又称作二部图，是图论中的一种特殊模型。

设G=(V, E)是一个无向图。如果顶点集V可分割为两个互不相交的子集X和Y，并且图中每条边连接的两个顶点一个在X中，另一个在Y中，则称图G为二分图。

二分图性质

定理：当且仅当无向图G的每一个回路的次数均是偶数时，G才是一个二分图。如果无回路，相当于任一回路的次数为0，故也视为二分图。

二分图判断

如果一个图是连通的，可以用如下的方法判定是否是二分图：
在图中任选一顶点v，定义其距离标号为0，然后把它的邻接点的距离标号均设为1，接着把所有标号为1的邻接点均标号为2（如果该点未标号的话），如图所示，以此类推。
标号过程可以用一次BFS实现。标号后，所有标号为奇数的点归为X部，标号为偶数的点归为Y部。
接下来，二分图的判定就是依次检查每条边，看两个端点是否是一个在X部，一个在Y部。
如果一个图不连通，则在每个连通块中作判定。

二分图匹配

给定一个二分图G，在G的一个子图M中，M的边集{E}中的任意两条边都不依附于同一个顶点，则称M是一个匹配。
匹配的数量等于E的边数量。下图加粗红色的是一个边数量为2的匹配。

最大匹配

G的所有子图中边数量最大的匹配成为最大匹配。如上图所示例子，最大边数为3的子图只有一种：

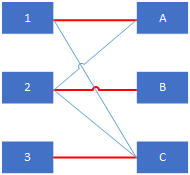
完全匹配（完备匹配）

对于数量较少的子集（如上图L或者R），子集中的每个顶点都和子图中的某条边关联，则称该子图所构成的匹配为完全匹配。

完全匹配一定是最大匹配，反过来则不一定。

本质上就是给数量较少的子集所有元素都给匹配了。

研究二分匹配的问题是为了寻找最大匹配，如何寻找？借助增广路径

增广路径的定义

增广路径的定义：设M为二分图G已匹配边的集合，如下图所示红色边

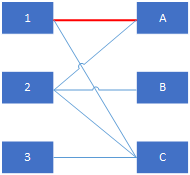
若P是图G中一条连通两个未匹配顶点的路径（P的起点在X部，终点在Y部，反之亦可），并且属M的边和不属M的边(即已匹配和待匹配的边)在P上交替出现，则称P为相对于M的一条增广路径。如下图黄红色路径2-A-1-C

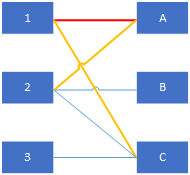
增广路径是一条“交错轨”。

它的第一条边和最后一条边都是目前还没有参与匹配的。因为路径的起点和终点还没有被匹配。

这样交错进行，显然P有奇数条边，因为路径中不存在回路，总共有偶数个顶点。并且属于M的边数比不属于M的边数少1。

匹配增广

当我们找到一条增广路径时，当我们把路径上属于M（已经匹配的边集合）的边从M中除去，并加入路径上不属于M的边，此时，增广路径中已经匹配的顶点依然是匹配状态，而未匹配的顶点也被匹配了，总的匹配边数加1。

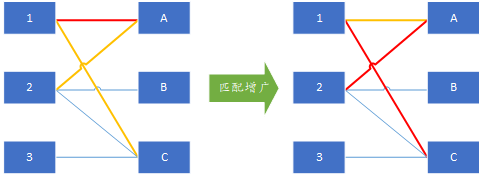
寻找增广路径

既然可以通过增广路径的匹配增广操作增加匹配的数量，接下来的问题是在已有的匹配基础上如何搜索到一条合适的增广路径

如下图所示红色线是已有的匹配

那么我们通过遍历左边点集合中未匹配的点，来找所有可用的增广路径，顶点1已经匹配了，接下来以未分配的左顶点2为增广路径的开始点，在右边依次遍历所有可能的顶点，如果找到是一个未分配的顶点如A点，那么这就是一条增广链2-A，通过增广操作可以得到如下图所示分配

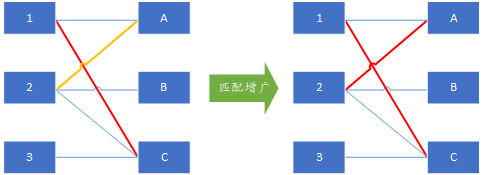
接下来以左边顶点3为开始点搜索增广链，3唯一连接的是右边的C，因此按照增广链的定义，唯一的增广链为3-C-1-A-2-B，通过增广操作得到最大匹配：

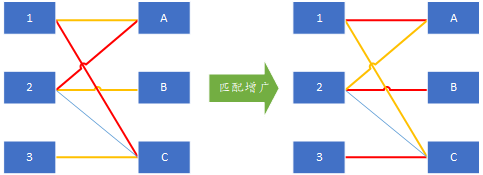
匈牙利算法的终止条件

当从左边集合中的某一点开始

没有搜索到任何的增广路径

这说明该点不是最大匹配必要的点

加入该点后匹配不能增广

如何证明

命题1、（在当前匹配下）没有搜索到增广链就说明该点不是最大匹配的必要点？或者说没有找到增广链，该匹配就是最大匹配？

命题2、在目前的匹配情况下，没有搜索到以该点 $u_{k+1}$ 开始的增广路径，在后面加入别的点的匹配情况下，也不可能有以该点开始的增广路径存在

这个两个问题非常重要

参考匈牙利算法原著……我暂时没看懂，后面看懂了更新

H.W. Kuhn. The Hungarian method for the assignment problem. Naval Research Logistics Quarterly, 2:83–97, 1955.

定理：存在增广链是增广当前匹配的充要条件

等价的命题是，为什么在当前匹配下不存在以左边某一未匹配点开始的增广链，该点就不是当前匹配下增广的必要点，即该点不能增广当前匹配。

从匹配增广的原理可以看出，以该点开始的增广链是该点可以增广当前匹配的充分条件

必要条件？

首先能理解的是：如果增广路径从左边开始终止在左边点

路径上已经选择的边和没有被选择的边数量相同

按照前面介绍进行增广操作并不能增加比配边数

然后用反证法去证明如果该点能改善匹配，那么就一定存在，不需要改变原来匹配点集合的（已经匹配的点一定在改善后的匹配中），以该点开始的增广链

在这里假设已经匹配的左边点为 $u_1,u_2,\dots u_k$ ，对应的右边点为 $v_1,v_2,\dots v_k$

如果该点 $u_{k+1}$ 能改善匹配，那么根据匹配的独立性，必然在改善后的匹配中，右边也有 $k+1$ 个点，而且，只需要一个新的右边点 $v_{k+1}$ 加入匹配即可（这个可以从下面的分析中可以看出）

1.如果在改善的匹配中， $u_{k+1}$ 匹配的是新点 $v_{k+1}$ ，那么 $u_{k+1}-v_{k+1}$ 就是一条增广链

2.如果 $u_{k+1}$ 匹配的不是新点 $v_{k+1}$ ，那么假设 $u_{k+1}$ 匹配的是 $v_{j}$ ， $v_{j}$ 在原来匹配中匹配对象是 $u_{j}$ ，根据匹配唯一性，在改善后的匹配中 $u_{j}$ 匹配的肯定不是 $v_{j}$ ，如果 $u_{j}$ 匹配的是新点 $v_{k+1}$ ，那么 $u_{k+1}-v_{j}-u{j}-v_{k+1}$ 就是一条增广链

3.如果 $u_{j}$ 匹配的还是原来匹配的点，那就继续上面的分析2，根据已经匹配点数量是有限的，当分析到最后一个左边点时，根据匹配的唯一性，它必然和新点 $v_{k+1}$ 连接（因为旧点只有k个），那么增广链依然存在（ $u_{k+1}$ 开始， $v_{k+1}$ 结束，中间穿过所有的 $u_1,u_2,\dots u_k$ 和 $v_1,v_2,\dots v_k$ ）

综上分析，如果存在改善匹配包含了该新点，那么就必然存在一条以该点开始的增广链，而且新增的右边点仅仅有一个，不需要另外的点去替换原来的右边点

引理：那么根据存在增广链是增广当前匹配的充要条件，算法只要遍历所有未匹配的左边点，没有找到增广链，即可终止算法，找到最大匹配

另外一方面

定理：在目前的匹配情况下

没有搜索到以该点 $u_{k+1}$ 开始的增广路径

在后面加入别的点的匹配情况下，也不可能有以该点开始的增广路径存在

（这个保证了算法只要遍历一遍左边点即可，不需要重复遍历）

证明：

原来的匹配 $M$ 为 $u_1,u_2,\dots u_k$ ，对应的右边点为 $v_1,v_2,\dots v_k$

如果加入新点 $u'$ 和 $v'$ 时，所使用的增广链为 ${\color{Purple} u'-v_{j_1}-u_{j_1}-\cdots-v_{j_m}-u_{j_m}-v'}$ ，改善后的匹配 $M'$ 变成 $u_1,u_2,\dots u_p$ 和对应的 $v_1,v_2,\dots v_p$ ，p=k+1

前提： $u_{k+1}$ 在原来的匹配下没有增广路径

假设 $u_{k+1}$ 在改善后的匹配下存在增广路径

1、如果增广路径 ${\color{Red} u_{k+1}-v_{l_1}-u_{l_1}-\cdots-v_{l_n}-u_{l_n}-v_{k+1}}$ 中不存在， ${\color{Purple} u'-v_{j_1}-u_{j_1}-\cdots-v_{j_m}-u_{j_m}-v'}$ 中的 $v$ ，那么增广路径肯定不存在 $u'$ ，因为改善匹配中存在匹配 $u'-v_{j1}$ ，所以

${\color{Red} u_{k+1}-v_{l_1}-u_{l_1}-\cdots-v_{l_n}-u_{l_n}-v_{k+1}}$ 中的 $u_l$ 和 $v_l$ 都是原匹配 $M$ 中的，因此这是原匹配中的一条增广路径，和前提相悖

2、如果增广路径 ${\color{Red} u_{k+1}-v_{l_1}-u_{l_1}-\cdots-v_{l_n}-u_{l_n}-v_{k+1}}$ 中存在， ${\color{Purple} u'-v_{j_1}-u_{j_1}-\cdots-v_{j_m}-u_{j_m}-v'}$ 中的 $v$ ，那么原匹配中必然存在增广路径 ${\color{Red} u_{k+1}-v_{l_1}-u_{l_1}-\cdots-v_{l_p}-u_{l_p}}-{\color{Purple}v_{j_q}-u_{j_q}-\cdots-v_{j_m}-u_{j_m}-v' }$ ，也是原匹配中的一条增广路径，和前提相悖

综上即证

上面的两条命题成立

当增广路径搜索算法，遍历一遍左边顶点集合后

已经加入最大匹配的点已经加入

没有加入的，也不可能通过加入该点增广匹配了

匹配已经达到最大，算法终止

C++算法代码

#include<iostream>
#include<cstring>
using namespace std;
const int maxn = 3;
int n = maxn, m = maxn;
int Map[maxn][maxn];//map[i][j]=1表示X部的i和Y部的j存在路径,是否可以匹配
int cx[maxn], cy[maxn];
bool vis[maxn];
//cx[i]表示X部i点匹配的Y部顶点的编号
//cy[i]表示Y部i点匹配的X部顶点的编号

bool dfs(int u)//dfs进入的都是X部的点
{
	for (int v = 0; v < n; v++)//枚举Y部的点，判断X部的u和Y部的v是否存在路径
	{
		//如果存在路径并且还没被标记加入增广路
		if (Map[u][v] && !vis[v])//vis数组只标记Y组
		{
			//标记加入增广路
			vis[v] = 1;

			//如果Y部的点v还未被匹配
			//或者已经被匹配了，但是可以从v点原来匹配的cy[v]找到一条增广路
			//说明这条路就可是一个正确的匹配
			//因为递归第一次进入dfs时，u是未匹配的
			//如果v还没有匹配对象，即和它相连的所有边都不在，已经选择的匹配边集合M（M\in E）中，这时就找到了u-v增广路径
			//如果v已经有匹配对象了，那么u-v是一条未选择的边，而v-cy[v] \in M 则是一条已经选择的边, dfs(cy[v])从cy[v]开始搜索增广路径
				//如果新的v'没有匹配对象，那么u-v-cy[v]-v'就是一条增广路径，如果v'已经有匹配对象了，那么根据匹配是唯一的，cy[v]-v'一定不在已经选择的边中(和cy[v]-v冲突)，u-v-cy[v]-v'-cy[v']符合增广路径对边顺序的要求，继续利用dfs(cy[v'])搜索u-v-cy[v]-v'-cy[v']-下面的点
				//当搜索到增广链时，如u-v-cy[v]-v',那么经过递归的匹配调整和return 1，进行匹配增广操作，假设dfs0 是main调用的dfs算法，dfs1是dfs0调用的dfs算法
				//在dfs1中进行cy[v]-v'的匹配，因为dfs1返回1，因此在dfs0中进行u-v的匹配，匹配增广操作的结果是{cy[v]-v}->{u-v,cy[v]-v'}
				//如果在一个dfs(k)自调用的dfs(k+1)中，遍历所有的v(k+1),要么已经有匹配点了，要么和输入u(k+1)没有连接可能，这时搜索终止，说明不存在经过u(k+1)的增广链，返回0
				//而在main调用的dfs(0)中，调用的dfs(1)返回的都是0，而且v都是已经有匹配了，那么不存在从该点出发的增广链，那么就该点就不在最大匹配当中
				//为什么找不到增广链就不在最大匹配当中呢？感觉可以用反证法证明，博客中下面内容可能有更新这方面的思考
			if (cy[v] == -1 || dfs(cy[v]))
			{
				cx[u] = v;//可以匹配，进行匹配
				cy[v] = u;
				return 1;
			}
		}
	}
	return 0;//不能匹配
}
int maxmatch()//匈牙利算法主函数
{
	int ans = 0;
	//匹配清空，全部置为-1
	memset(cx, -1, sizeof(cx));
	memset(cy, -1, sizeof(cy));
	for (int i = 0; i < n; i++)
	{
		if (cx[i] == -1)//如果X部的i还未匹配
		{
			memset(vis, 0, sizeof(vis));//每次找增广路的时候清空vis
			ans += dfs(i);
		}
	}
	return ans;
}

int main_test()
{
	//输入匹配的两个点集合的数量
	cin >> n >> m;
	//输入两个点集合成员间的匹配可能
	int x, y;
	for (int i = 0; i < m; i++)
	{
		cin >> x >> y;
		Map[x][y] = 1;
	}
	//执行匈牙利算法，输出最大匹配
	cout << maxmatch() << endl;
}

匈牙利算法证明+原理+C++代码

介绍

二分图