改进csp回溯算法性能的一个基本观点是,局部不一致会导致大量的抖动或无效率的搜索[47,89]。局部不一致性是某些变量的实例化,这些变量满足相关约束,但不能扩展到一个或多个额外变量,因此不能成为任何解决方案的一部分。(局部不一致不是好事;参见4.4节)。如果我们使用回溯搜索来寻找解决方案,这种不一致性可能导致搜索中出现许多死区,并导致许多徒劳的搜索工作。这种见解导致:
- 描述CSP局部一致性水平的条件的定义
- 约束传播算法的发展——这些算法通过消除CSP中的不一致性来加强这些级别的局部一致性
- 有效的回溯算法寻找解决csp的方案,保持在搜索局部一致性水平
在回溯搜索中维护局部一致性的一般方案是在搜索树中的每个节点上执行约束传播。约束传播算法通过发布排除或消除不一致的附加约束来消除局部不一致。当在搜索过程中使用时,约束会随着搜索在树中的深入而在节点上发布。但是在对某个节点进行回溯时,必须撤销在该节点上发布的约束。当在执行任何实例化或分支决策之前在搜索树的根节点上使用时,约束传播有时称为预处理阶段preprocessing。
结合约束传播的回溯搜索有两个重要优点。首先,在搜索过程中消除不一致可以通过消除许多死端和简化剩余的子问题来显著地修剪搜索树。在某些情况下,一个变量在约束传播后会有一个空域;也就是说,没有值满足该变量的一元约束。在这种情况下,可以启动回溯,因为在搜索树的这个分支上没有解决方案。在其他情况下,变量的域将被缩小。如果一个域被简化为一个值,那么该变量的值是强制的,将来不需要对其进行分支。因此,在约束传播之后可以更容易地找到CSP的解决方案,或者表明CSP没有解决方案。其次,一些最重要的变量排序启发式利用约束传播收集的信息来做出有效的变量排序决策(这将在4.6节中进一步讨论)。由于这些优点,现在标准的回溯算法包含某种形式的约束传播。
局部一致性的定义至少可以分为两类。首先,根据定义中的基本实体,可以将定义分为基于约束的定义和基于变量的定义。其次,局部一致性的定义可以按照约束传播过程中是否只需要发布一元约束,或者是否有时需要发布更高层次的约束来分类。在回溯的实现中,变量的域是可扩展表示的,通过更新域的表示可以非常有效地发布和撤销一元约束。在更高的高度上发布和撤回限制是不那么容易理解的,而且代价更大。如果只需要一元约束,则约束传播有时称为域过滤或域修剪。
将某种形式的约束传播合并到回溯算法中的想法来自几个方向。Davis和Putnam[31]提出了单位传播(unit propagation),这是一种专门用于SAT的约束传播形式。Golomb和Baumert[57]可能是第一个非正式地描述通过在搜索过程中加入某种形式的域修剪来改进一般回溯算法的想法的人。Fikes的rf - arf[37]和Lauriere的Alice[82]使用了约束传播技术,这两种语言都用于陈述和求解csp。Gaschnig[47]是第一个提出回溯算法的人,该算法强制精确定义了每个节点的local一致性级别。Gaschnig的算法使用了d路分支。Mackworth[89]概括了Gaschnig提出的回溯算法,该算法将case-analysis与约束传播交叉(参见[89]获取更多的历史参考资料)。
自这项早期工作以来,出现了大量关于约束传播和局部一致性的文献;超出了我可以合理讨论的范围。因此,我选择了两个具有代表性的例子:arc consistency和strong k-consistency。这些局部一致性说明了上面给出的不同分类。同时,弧一致性是目前实践中最重要的局部一致性,也是目前最受关注的局部一致性,而强k一致性在csp的理论方面发挥了重要作用。对于这些例子,我给出了局部一致性的定义,然后讨论了在搜索过程中保持这种级别的本地一致性的回溯算法。我不讨论任何特定的约束传播算法。本手册有两章专门讨论这个主题(见第三章和第六章)。注意,许多约束传播算法的表示都是针对将在预处理阶段使用该算法的情况。但是,当在搜索过程中使用以保持一定程度的本地一致性时,对约束传播算法的连续调用之间通常只会发生很小的变化。因此,人们也付出了很大的努力,使这种算法逐渐增多,因此在搜索过程中使用时效率更高。在提出结合约束传播的回溯算法时,我给出了回溯算法的“纯”形式,即在搜索树的每个节点上保持一致的局部一致性。这只是为了便于表达。在实践中,局部一致性的实施水平和实施算法是特定于每个约束的,并且在约束之间是不同的。一个例子是被广泛使用的全不同全局约束,其中快速算法被设计用于强制执行许多不同级别的局部一致性,包括圆弧一致性、范围一致性、边界一致性和简单的值移除。然后,由建模人员决定执行哪一级的本地一致性。
4.3.1 Backtracking and Maintaining Arc Consistency
Mackworth [89,90]定义了一种称为弧一致性的局部一致性。 给定约束C,符号t∈C表示元组t-对值(C)中的每个变量的值的赋值 - 满足约束C.符号t [x]表示由元组t分配给变量x的值。
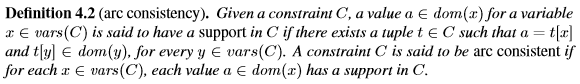
通过反复从约束的变量域中删除不受支持的值,可以使约束保持一致。请注意,本地一致性的定义是基于约束的,在CSP上强制执行arc一致性意味着迭代约束,直到不再对域进行任何更改为止。加强arc一致性的算法已经被广泛研究(见第3章和第6章)。对于任意约束的优化算法,最坏情况下的时间复杂度为,其中r为约束的浓度,d为变量域的大小[101]。幸运的是,对于实践中出现的约束类,几乎总是可以做得更好。例如,在最坏的情况下,可以使所有不同的约束在
时间内保持一致。Gaschnig[47]建议在回溯搜索过程中保持圆弧一致性,并给出了第一个包含此思想的显式算法。在Sabin和Freuder[116]之后,我将用MAC表示这种算法。MAC算法对至少一个未实例化变量的约束保持arc一致性(见表4.1)。在搜索树的每个节点上,对CSP应用了一种增强圆弧一致性的算法。由于arc一致性是在节点的父节点上强制执行的,所以最初的约束传播只需要在分支策略发布的约束上强制执行。反过来,这可能导致其他约束变得不一致,并且约束传播将继续,直到不再对域进行任何更改为止。如果由于约束传播,域变为空,则分支为死端并被拒绝。如果没有域是空的,则接受该分支,搜索将继续到下一个级别。

作为应用MAC的一个例子,考虑图4.1所示的6皇后问题的回溯树。MAC只访问节点25,因为它发现这个节点是一个死端。图4.2a中的板显示了约束传播的结果。带阴影的带数字的正方形对应于通过约束传播从变量域中移除的值。如果由于树的第i层的赋值而将值移除,则将值i放置在阴影正方形中。可以看出,在约束传播之后,一些变量的域是空的。因此,赋值集{x1 = 2,x2 = 5}不能成为CSP解决方案的一部分。

当在搜索过程中维护arc一致性时,从变量域中删除的任何值都不参与CSP的任何解决方案。然而,并不是域中的所有值都一定是某个解决方案的一部分。因此,圆弧一致性传播虽然可以减少搜索空间,但不能消除所有可能的死端。假设如果变量域中的每个值都是CSP的某个解决方案的一部分,那么CSP的域是最小的。显然,如果约束传播只会在搜索树的每个节点上留下最小的域,那么搜索将是自由回溯的,因为所选择的任何值都将导致解决方案。不幸的是,找到最小域至少与解决CSP一样困难。在对单个约束施加arc一致性之后,变量域中的每个值都是单独考虑的约束的某个解决方案的一部分。找到最小域就相当于对CSP中约束条件的结合强制求弧一致性,这个过程在最坏情况下是n的指数,即CSP中的变量数量。因此,圆弧一致性可以看作是逼近最小域。
总的来说,在搜索树的每个节点上的约束传播的成本,和最小域的近似的质量之间有一个权衡。一种改进这种近似的方法是使用更强的局部一致性,例如单例一致性(参见第3章),但是会增加约束传播的成本。降低约束传播成本的一种方法,就是对最小的区域进行较差的近似,并增加整体搜索成本的增加,实际上就是限制弧一致性的应用。其中一种算法称为前向检查。前向检查算法(FC)在约束条件上保持arc的一致性,而约束条件恰好是一个未实例化的变量(见表4.1)。在这些约束条件下,可以在O(d)时间内强制实现arc的一致性,其中d是未实例化变量的域的大小。Golomb和Baumert[57]可能是第一个非正式地描述前向检查(在[57]中称为排除)的人。McGregor[93]、Haralick和Elliott[63]给出了第一个显式算法。前向检查最初是为二进制约束提出的。这里使用的对非二进制约束的推广是由于Van Hentenryck[128]。
作为应用FC的一个例子,考虑图4.1所示的回溯树。FC只访问节点25、253、2531、25314和2536。图4.2b的板子显示了约束传播的结果。搜索过程中留下的空格对应于FC访问的节点。
该领域的早期实验工作发现,FC远优于MAC[63,93]。然而,这种优势在一定程度上是基准测试的易用性造成的。同时,近年来弧线一致性传播算法也得到了许多实际的改进,特别是在增量方面。结果表明,回溯算法在搜索过程中保持了完整的圆弧一致性,在实践中被认为是非常重要的。一个例外是广泛使用的DPLL算法[30,31],这是一种专门针对CNF格式SAT问题的回溯算法(见表4.1)。DPLL算法采用单元传播,有时称为布尔约束传播,作为其约束传播机制。可以看出,单位传播等价于对SAT问题的前向检验。进一步可以看出,弧一致性对这些问题的修剪量与前向检验的修剪量相等。因此,前向检查是SAT问题上的约束传播的正确水平。
前向检验只是限制电弧一致性传播的一种方法;许多变化是可能的。例如,可以对具有不同数量的未实例化变量的约束保持arc一致性。Bessi 'ere等人考虑了这些可能性。在指定应该传播哪些约束时,还可以考虑未实例化变量的域的大小。作为第三种选择,可以对约束传播算法本身以及它如何遍历约束设置特别的限制[63,104,117]。
另一种限制弧一致性应用的方法是限制弧一致性的定义,这种方法可以通过限制传播哪些约束来实现,也可以通过限制传播本身来实现。一个重要的例子是边界一致性。假设变量的域又大又有序,并且变量的域由区间(域内的最小值和最大值)表示。使用边界的一致性,而不是要求每个值∈dom(x)支持的约束,我们只问最小值和最大值都有一个支持的约束。虽然一般来说,边界一致性比弧一致性弱,但已经证明边界一致性对于算术约束和全局约束是有用的,因为它有时可以更有效地执行(详细信息请参阅第3章和第6章)。例如,在最坏的情况下,在O(r)时间内alldifferent都可以使边界一致,相比于弧一致性的O(r2d),其中r是约束的浓度,d是变量域的大小。此外,对于一些问题,可以证明弧一致性所执行的修剪量与边界一致性所执行的修剪量是相等的,因此不需要偿还弧一致性所带来的额外成本。
4.3.2 Backtracking and Maintaining Strong k-Consistency
Freuder[39,40]定义了一种称为强k-一致性的局部一致性级别。如果满足由赋值集实例化的所有变量的每个约束,那么赋值集就是一致的。

对于二进制csp的特殊情况,强2一致性与弧一致性相同,强3一致性也称为路径一致性。CSP可以通过反复检测并消除所有的不一致性t = {x1 = a1,…,xj−1 = aj−1 } 1≤j < k,t是一致的但不能扩展到某些第j个变量xj。删除不一致或nogood t,约束发布规则的元组的CSP t。实施强有力的k-consistency可能大大增加的数量限制在CSP,随着新的约束可以在k指数。一旦一个CSP已经强烈k-consistent任何价值仍在变量的域可以扩展到一组一致的作业/ k变量backtrack-free的方式。但是,除非k = n,否则不能保证一个值可以扩展到所有n个变量的解。在含有任意约束条件的CSP上执行强k一致性的最优算法具有O(nkdk)最坏情况时间复杂度,其中n是CSP中的变量数量,d是变量[29]的域大小。
假设MCk是在搜索过程中保持强k一致性的算法(见表4.1)。为了指定MCk,我假设分支策略是枚举的,因此,搜索树中的每个节点都对应一组赋值。在搜索过程中,我们希望维护这样一个属性,即变量域中的任何值都可以扩展到k个变量上的一致赋值集。要做到这一点,我们必须在概念上通过修改约束来考虑当前的赋值集。给定一组赋值t,只选择约束中与t中的赋值一致的元组,然后将这些元组投影到约束的未实例化变量集上,以给出新的约束(详细信息请参见[25])。在这种体系结构下,FC可以看作是保持一种一致性,而对于二进制csp, MAC可以看作是保持强二一致性。
这样的架构对于k > 2是否可行?有证据表明答案是肯定的。Van Gelder和Tsuji[127]提出了一种保持二元子句(两个文本子句)分辨率封闭性的算法,实验证明该算法在较大的SAT实例上可以比DPLL快得多。该算法可以看作是专门针对SAT的MC3算法。Bacchus[2]在此工作的基础上,证明了所得到的SAT算法具有较强的鲁棒性,与最先进的DPLL算法具有竞争力。考虑到已经有大量的工程投入到DPLL的求解中,这一点是值得注意的。然而,到目前为止,虽然已经作出了努力,但还没有令人信服的证据证明一般的战略文件具有相应的结果。