局部一致性是一种正式定义我们希望网络保证的一致性数量的方法，因此，执行这种一致性级别的算法将决定生成哪个网络。但是没有提到算法是如何执行的。规则迭代在另一方面解决了这个问题。约简规则指定在哪些条件下以及在哪些约束条件下执行筛选操作。只有当约简规则及其应用方式具有一些良好的性质时，网络生成的结果才能保证具有一定程度的局部一致性等形式化性质。规则迭代方法最初由Montanari和Rossi以松弛规则的名义正式提出[96]。Benhamou等通过区间算法interval arithmetics(即只减少边界)研究规则迭代[10,11]。约束处理规则(Constraint Handling Rules, CHR)是一种基于约简规则的编程语言(参见第二部分的[59]和第13章)。我基本上遵循Apt关于约简规则概念的表述。

约简规则只是一个将网络映射到另一个网络的函数，其中图像是输入的收紧。

我们应该记住PN包含了所有紧绷N的网络(见定义3.13)。在大多数情况下，约简规则是根据单个约束减少单个变量域的约简步骤。我将它们命名为传播器。

传播器可以验证一些属性。

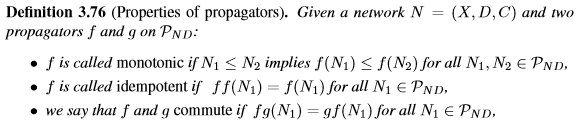
1）单调性  2）幂等  3）可交换

实践中使用的大多数传播器都满足定义3.76的特性。其中单调性尤为有趣。我首先需要定义迭代和传播器稳定性的含义。

PND中可能有许多网络对于给定的传播器集是稳定的。但传播子的单调性意味着只会产生其中的一个。

算法3.8是以网络N和PND上的一组传播子F作为输入的过程。由于3.80号提案，我们保证它会终止。如果f中的所有f都是单调的，则算法3.8的输出是f在N上的最小固定点。

有时，除了单调性之外，传播子还具有其他一些特性。在这些情况下，算法3.8可以被简化，同时仍然保证产生相同的结果。

通过定义适当的传播器集，我们可以获得前几节中介绍的大部分局部一致性。例如，我们可以在网络N =(X,D,C)上实施弧一致性。我首先定义传播器fi,j，使:

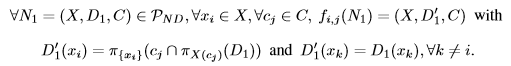
它们都是单调的。然后，泛迭代(N,FAC)终止于FAC的最小固定点，即N的圆弧一致闭包。

从[2]中可以看出，我们还可以通过定义同时涉及多个约束并改变约束集的单调传播器集来增强高阶一致性，例如路径一致性。