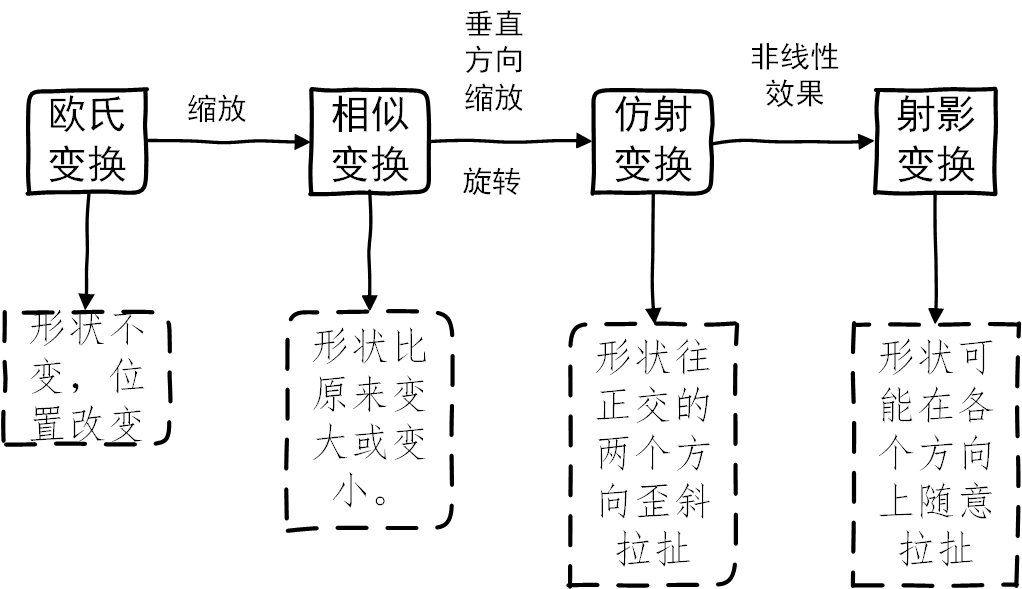
MVG学习笔记(11) --变换层次

  射影变换组成一个群，称为射影线性群。

   $n\times n$可逆实矩阵为一般线性群,称为 $GL(n)$。将相差纯量因子矩阵视为等同得到射影线性群 $PL(n)$，是 $GL(n)$的商群。

   $PL(3)$的重要子群有仿射群和欧式群。仿射群是 $PL(3)$中最后一行为 $(0,0,1)$的矩阵组成的子群；欧氏群是仿射群的子群，左上角 $2\times 2$矩阵是正交的，若该矩阵行列式为1，则为定向欧氏群。

图1，在中心投影下的失真，瓷砖地板的图像。 （a）相似变换：圆似圆，方似方。 平行或垂直的线在图像中相同定向。 （b）仿射：圆成椭圆。 世界垂直线不再是垂直线。 然而，平行依旧平行。 （c）射影：平行线变成会聚线。 靠近相机的瓷砖比远处的瓷砖更大。

  不变量。 将变换视为作用于点或曲线的坐标的矩阵的代数方法，其中保持不变元素或量为不变量，用以介绍变换。 几何配置的（标量）不变量是配置的函数，其值通过特定变换而不变。 例如，两个点的距离在欧式变换（平移和旋转）不变，而相似变换（例如平移，旋转和均匀缩放）下不保持。 因此，距离是欧式不变量，但不是相似不变量。 两线的夹角既是欧式又是相似不变量。

等距变换(Isometries)

  等距变换是平面 $\mathcal{IR}$的变换，保持欧式距离不变（ios=一样，metric=度量）。

  等距变换可以表示为：

$\begin{pmatrix}x^\prime\\y^\prime\\1\end{pmatrix}=\begin{bmatrix}\varepsilon \cos\theta&-\sin \theta&t_x\\\varepsilon\sin \theta&\cos \theta&t_y\\0&0&1\end{bmatrix}\begin{pmatrix}x\\y\\1\end{pmatrix}$

  其中 $\varepsilon=\pm1$，如果 $\varepsilon =1$则等距变换是保向的切是欧氏变换（平移和旋转的复合），反之是逆向的。例如反射(又对角矩阵 ${\rm diag}(-1,1,1)$表示)与欧氏变换的复合。

  欧氏变换是刚体运动模型，是最重要的等距变换，而保向等距变换在结构恢复时出现多义性。

  平面欧氏变换用简洁分块形式写成：

$\rm x^\prime=H_Ex=\begin{bmatrix}\rm R&\rm t\\\boldsymbol{0}^T &1\end{bmatrix}x$

  其中 $R$是 $2\times 2$旋转矩阵（满足 $R^TR=RR^T=I$的正交矩阵）, $\rm t$是二维平移矢量，而 $\boldsymbol{0}^T$是二维零矢量。特殊情况是纯旋转( $\rm t=0$)和纯平移( $R=I$)。欧氏变换也称为移位(displacement)。

  平面欧氏变换有三个自由度：旋转占一个，平移占两个。因此必须制定三个参数才能确定该变换。可以由两组点对应来计算该变换。

旋转的自由度是角度 $\theta$，平移是两个轴方向上的位移量

  不变量 长度（两点间距离），角度（两线夹角）和面积。

  群和定向。 如果左上方 $2\times 2$矩阵具有行列式1，则等距变换是保向的。保向的等距形成一个群，而方逆向的等距则不是。 这种区别也适用于相似变换和仿射变换的情况。

相似变换(Similarity transformations)

  相似变换是一个等距变换与一个均匀缩放的复合。当欧氏变换（没有反射）与均匀缩放复合时，相似变换矩阵表示为：

$\begin{pmatrix}x^\prime\\y^\prime\\1\end{pmatrix}=\begin{bmatrix}s \cos\theta&-s\sin \theta&t_x\\s\sin \theta&s\cos \theta&t_y\\0&0&1\end{bmatrix}\begin{pmatrix}x\\y\\1\end{pmatrix}$

  以更简洁的矩阵分块形式写成：

$\rm x^\prime=H_sx=\begin{bmatrix}{\mathcal{s}}\rm R&\rm t\\\boldsymbol{0}^T &1\end{bmatrix}x$

  其中 $s$表示均匀缩放。相似变换也才称等形变换，因为其保持“形状”。平面相似变换具有四个自由度（多出来缩放因子 $s$），可以由两组对应点算出。

  不变量：直线夹角（不受缩放影响），平行线依旧平行，两点间距离不是，但长度比率是（缩放因子互相抵消）。面积比率也是（缩放因子的平方被抵消）。

  度量结构：确定到只相差一个相似变换的结构。

仿射变换

  由一非奇异线性变换与一平移变换复合。矩阵表示为：

$\begin{pmatrix}x^\prime\\y^\prime\\1\end{pmatrix}=\begin{bmatrix}a_{11}&a_{12}&t_x\\a_{21}&a_{22}&t_y\\0&0&1\end{bmatrix}\begin{pmatrix}x\\y\\1\end{pmatrix}$

  或分块形式：

$\rm x^\prime=H_Ax=\begin{bmatrix}A&\rm t\\\boldsymbol{0}^T &1\end{bmatrix}x$

  其中 $A$是 $2\times 2$的非奇异矩阵(行列式不为0的满秩矩阵)。平面仿射变换有六个自由度，对于六个矩阵元素（前两行）,可以通过三组对应点来计算。

  仿射变换 $A$的几何效应看成是选择和非均匀缩放的复合，由SVD分解为：

$A=UDV^T=(UV^T)(UDV^T)=R(\theta)(R(-\phi)DR(\phi))\tag{1}$

  其中 $R(\theta)，R(\phi)$分布表示旋转角为 $\theta，\phi$的旋转，而 $D$为对角矩阵：

$D=\begin{bmatrix}\lambda_1&0\\0&\lambda_2\end{bmatrix}$

  仿射变换被看成是旋转 $\phi$，假设已选择的 $x$和 $y$的方向分别进行按比例因子 $\lambda_1$和 $\lambda_2$的缩放，再假设一个回转( $-\phi$)后最后一个旋转 $\theta$。与相似变换比，“新”几何仅仅是非均匀缩放，使得仿射变换比相似变换多两个自由度。它们是缩放方向的角度 $\phi$和缩放参数比率 $\lambda_1:\lambda_2$。

  仿射变换的本质是特定角的两个垂直方向进行缩放。

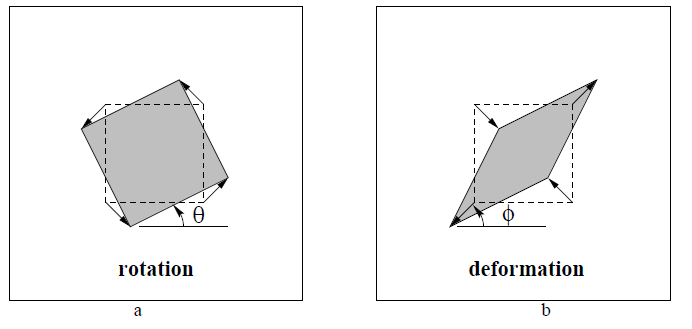
平面仿射变换失真：（a)旋转 $R(\theta)$；（b)形变 $R(-\phi)DR(\phi)$，注意形变方向是正交的。

不变量:

（1）平行依然平行：相交的无穷远点被映射到另一个无穷远点。

（2）平行线段长度比：直线段长度缩放仅与该线段方向和缩放方向之间夹角有关。假定线段与正交缩放方向 $x-$轴的夹角为 $\alpha$，那么缩放大小为 $\sqrt{\lambda_1^2\cos^2\alpha+\lambda_2^2\sin^2\alpha}$,该缩放因子对所有同向直线一样，所以平行线比率中被抵消。

（3）面积比。从公式（1）分解式得到该不变性。旋转和平移不影响面积，起作用的是 $\lambda_1,\lambda_2$的缩放，效果是面积被缩放了 $\lambda_1\lambda_2=\det A$倍。面积比该因子被抵消，然而在射影变换中不成立。

  根据 $\det A$的正负判断仿射变换是保向还是逆向的。

射影变换

  射影矩阵的矩阵表达为：

$\begin{pmatrix}x^\prime_1\\x^\prime_2\\x^\prime_3\end{pmatrix}=\begin{bmatrix}h_{11}&h_{12}&h_{13}\\h_{21}&h_{22}&h_{23}\\h_{31}&h_{32}&h_{33}\end{bmatrix}\begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}$

  是其齐次坐标的一般非奇异线性变换，是仿射变换的推广，仿射变换是非齐次坐标的一般非奇异线性变换加上平移的复合，其矩阵分块形式为：

$\rm x^\prime=H_Px=\begin{bmatrix}A&\rm t\\\boldsymbol{\rm v}^T &v\end{bmatrix}x$

  其中矢量 $v=(v_1,v_2)^T$。齐次矩阵九个元素仅它们之间比率有意义，自由度为8。并不是总有可能通过对矩阵缩放而取 $v$为1，因为 $v$可能是0。两平面的射影变换可由四组点对应计算，但属于同一平面的三点必须不共线。

  不变量：四共线点的交比，即直线上长度的交比；

图2：射影变换下的四个共线点交比不变

  注意图2，点 $A，B，C，D$和 $A'，B'，C'，D'$通过投影变换相关，因此它们的交比 $（A，B; C，D）$和 $（A'，B'; C' ，D'）$是平等的。

$（A，B; C，D）=\frac{AC\cdot BD}{BC\cdot AD}$

射影变换的分解

  射影变换可以分解为一串变换链的复合，链中每个句子比其一个矩阵所表示的变换层次高。

$\rm H=H_sH_AH_p=\begin{bmatrix}{\mathcal{s}}\rm R&\rm t/{\mathcal v}\\\boldsymbol{0}^T &1\end{bmatrix}\begin{bmatrix}K&\boldsymbol{0}\\\boldsymbol{0}^T &1\end{bmatrix}\begin{bmatrix}1&\boldsymbol{0}\\\boldsymbol{\rm v}^T &{\mathcal v}\end{bmatrix}=\begin{bmatrix}A&\boldsymbol{t}\\\boldsymbol{\rm v}^T &{\mathcal v}\end{bmatrix}$

  其中 $\rm A= {\mathcal s}RK+\boldsymbol{\rm tv^T}/{\mathcal v}$,而且 $\rm K$满足 $\det K=1$的归一化上三角矩阵。如果 $v \neq 0$则上述分解有效，而且如果 $s$取正值，则还是唯一的。

   $\rm H_s,H_A,H_p$分别是相似变换、仿射变换和射影变换。 $\rm H_p$(2自由度)移动无穷远执行，属于有约束透视变换。 $\rm H_A$(2自由度)影响仿射性质而不移动无穷远线。 $\rm H_s$是一般相似变换（4自由度)，并不影响仿射和射影性质。

总结

群	矩阵	自由度	失真	不变性质
射影	$\begin{bmatrix}h_{11}&h_{12}&h_{13}\\h_{21}&h_{22}&h_{23}\\h_{31}&h_{32}&h_{33}\end{bmatrix}$	8		共点 共线 接触的阶：相交（一阶接触）；相切（二阶接触）；拐点（与直线的3阶接触）；切线不连续和奇点(cups)。交比（长度比的比）
仿射	$\begin{bmatrix}a_{11}&a_{12}&t_x\\a_{21}&a_{22}&t_y\\0&0&1\end{bmatrix}$	6		平行；面积比；体积比；共线线段或平行线段的长度比（如中点），矢量线性组合（如形心）。无穷远线 $\rm I_\infty$
相似	$\begin{bmatrix}s r_{11}&sr_{12}&t_x\\sr_{21}&sr_{22}&t_y\\0&0&1\end{bmatrix}$	4		长度比；夹角；虚圆点；体积比
欧氏	$\begin{bmatrix}r_{11}&r_{12}&t_x\\r_{21}&r_{22}&t_y\\0&0&1\end{bmatrix}$	3		长度；面积；体积

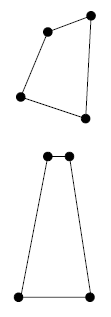
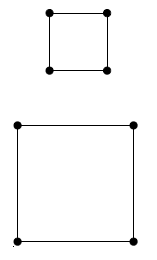
  仿射变换介于相似和射影之间，其推广相似变换使得夹角不再保持，造成物体形状变换后歪斜。仿射变换对平面作用是均匀的，平面上任何地方的物体（正方形）的面积缩放因子 $\det A$都一样。直线变换方向取决于其原来方向，而它在平面上位置无关。射影变换使得面积缩放随位置改变而改变（透视变换下，较远正方形比较近的正方形小，见图1）；且直线变换方向即取决于原线方向又取决于其位置。

  射影与仿射区别于射影中矢量 $\bold v$不是零，引起了射影变换的非线性效果。

  理想点 $(x_1,x_2,0)$在仿射和射影下映射作对比，仿射

$\begin{bmatrix}A&\rm t\\\boldsymbol{0}^T &1\end{bmatrix}\begin{pmatrix}x_1\\x_2\\0\end{pmatrix}=\begin{pmatrix}\rm A\begin{pmatrix}{\mathcal x_1}\\{\mathcal x_2}\end{pmatrix}\\0\end{pmatrix}$

  而射影

$\begin{bmatrix}A&\rm t\\\boldsymbol{\rm v}^T &v\end{bmatrix}\begin{pmatrix}x_1\\x_2\\0\end{pmatrix}=\begin{pmatrix}\rm A\begin{pmatrix}{\mathcal x_1}\\{\mathcal x_2}\end{pmatrix}\\v_1x_1+v_2x_2\end{pmatrix}$

  即仿射中理想点还在无穷远处，而射影却将之映射到有限点，因此其可以对消失点（灭点）建模。

  下面是博主自认为四者关系的观点，若是有误请提出。