• Hadamard变换

用于SATD的计算

Hadamard矩阵

只有1，-1构成的正交矩阵，例如
$H_2= \begin{bmatrix} 1 & 1 \\ 1 & -1 \\ \end{bmatrix}\\ H_4= \begin{bmatrix} 1 &1 &1 &1\\ 1 &-1 &1 &-1\\ 1 &1 &-1 &-1\\ 1 &-1 &-1 &1 \end{bmatrix}\\$

有hadamard矩阵的推导公式
$H_{2^{k+1}}= \begin{bmatrix} H_{2^k} & H_{2^k} \\ H_{2^k} & -H_{2^k} \\ \end{bmatrix}$

变换

有矩阵 $A_4$，则其hadamard变换为
$A'_4=H_4·A_4·H_4$

• DCT离散余弦变换

离散余弦矩阵：

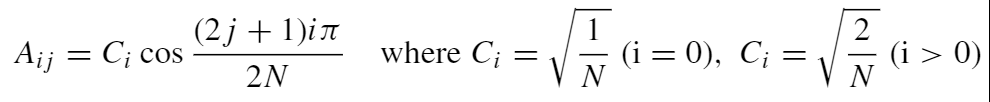
实例：

$DCT_4= \begin{bmatrix} 0.5000000 & 0.5000000 & 0.5000000& 0.5000000\\ 0.6532815& 0.2705981& -0.2705981& -0.6532815\\ 0.5000000 & -0.5000000 & -0.5000000& 0.5000000\\ 0.2705981& -0.6532815& 0.6532815& -0.2705981\\ \end{bmatrix}$

作用

将空域（space）的信号转换到频域（frequency）上，拥有良好的去矩阵相关性，为图像视频压缩后期的量化（Quantification）做前期准备，DCT变换本身是无损（lossless）的，但量化确实有损的。

过程

• FDCT（Forward DCT）
  有DCT的n阶矩阵 $M_n$，矩阵 $A_n$的FDCT变化为 $A'_n=M_n·A_n·M_n^T$
• IDCT（Inverse DCT）
  有DCT的n阶矩阵 $M_n$，矩阵 $A_n$的IDCT变化为 $A'_n=M_n^T·A_n·M_n$

效果

矩阵 $m$经过FDCT（Forward DCT）转换后的矩阵 $m'$，其左上角（即[0,0]位置）的值成为DC值，其余所有位置的值成为AC值。DC值可被看作该矩阵的均值，因为它与该矩阵的所有值都有关。

• 高频分量：
  距离DC越近的值（靠左上角的值）越大
• 低频分量：
  距离DC越远的值（靠右下角的值）越小，接近于0

图像的相关性越大，DCT转换后的效果越明显，即左上角大值，右下角趋于0
$FDCT( \begin{bmatrix} 13& 34& 205& 255\\ 9& 43& 198& 254\\ 11& 35& 207& 254\\ 9& 36& 210& 237\\ \end{bmatrix} )= \begin{bmatrix} 502.500000& -403.842775& 18.500000& 89.886112\\ 4.493714& -4.553301& 9.337282& -6.906854\\ -3.000000& 3.444151& -4.000000& 8.314916\\ 3.009408& -4.406854& 4.250312& 6.053301\\ \end{bmatrix}$
将一副图像分别进行 $FDCT_4$和 $FDCT_{16}$变换后：

能够发现每个块（block）的信息都堆积到了左上角

• 整数离散余弦变换

DCT变换的缺点

由于DCT变换中含有超越函数cos，没有任何机器可以精确的计算出它的值，不同的精确的会产生不同的误差，况且在DCT变换中还有求和操作（矩阵点乘中的行列乘积和），这样会导致误差的积累，进而最后的输出和输入不同，同时大量的浮点数计算使得计算量增大。

改进

DCT变换 $A'_n=M_n*A_n*M_n^T$中DCT矩阵 $M_n$的实质为
$M_n= \begin{bmatrix} a& a& a& a\\ b& c& -c& b\\ a& -a& -a& a\\ c& -b& b& -c\\ \end{bmatrix}\\ a=\frac{1}{2},b=\sqrt{\frac{1}{2}}cos(\frac{\pi}{8}),c=\sqrt{\frac{1}{2}}cos(\frac{3\pi}{8})$

扫描二维码关注公众号，回复： 4588118 查看本文章

改造下 $M_n$
$M_n= \begin{bmatrix} a& a& a& a\\ b& c& -c& b\\ a& -a& -a& a\\ c& -b& b& -c\\ \end{bmatrix}= \begin{bmatrix} a&b&a&b\\ \end{bmatrix} \begin{bmatrix} 1& 1& 1& 1\\ 1& \frac{c}{b}& -\frac{c}{b}& 1\\ 1& -1& -1& 1\\ \frac{c}{b}& -1& 1& -\frac{c}{b}\\ \end{bmatrix}=\mathbf{a}·M'_n$
则有
$A'_n=M_n·A_n·M_n^T= ( \begin{bmatrix} a&b&a&b\\ \end{bmatrix} \begin{bmatrix} 1& 1& 1& 1\\ 1& \frac{c}{b}& -\frac{c}{b}& 1\\ 1& -1& -1& 1\\ \frac{c}{b}& -1& 1& -\frac{c}{b}\\ \end{bmatrix} )·A_n·( \begin{bmatrix} 1& 1& 1& \frac{c}{b}\\ 1& \frac{c}{b}& -1& -1\\ 1& -\frac{c}{b}& -1& 1\\ 1& 1& 1& -\frac{c}{b}\\ \end{bmatrix} \begin{bmatrix} a\\ b\\ a\\ b\\ \end{bmatrix} )\\= \begin{bmatrix} 1& 1& 1& 1\\ 1& \frac{c}{b}& -\frac{c}{b}& 1\\ 1& -1& -1& 1\\ \frac{c}{b}& -1& 1& -\frac{c}{b}\\ \end{bmatrix} )·A_n·( \begin{bmatrix} 1& 1& 1& \frac{c}{b}\\ 1& \frac{c}{b}& -1& -1\\ 1& -\frac{c}{b}& -1& 1\\ 1& 1& 1& -\frac{c}{b}\\ \end{bmatrix} \bigotimes \begin{bmatrix} a^2& ab& a^2& ab\\ ab& b^2& ab& b^2\\ a^2& ab& a^2& ab\\ ab& b^2& ab& b^2\\ \end{bmatrix} \\=m'_n·A_n·m'^T_n\bigotimes Ef$
其中 $\bigotimes$表示矩阵对应相乘， $\frac{c}{b}=\frac{\sqrt{\frac{1}{2}}cos(\frac{3\pi}{8})}{\sqrt{\frac{1}{2}}cos(\frac{\pi}{8})}=0.4142136$，为了简化计算，令 $\frac{c}{b}=0.5$且为了保持矩阵的正交性修正
$b=\sqrt{\frac{2}{5}}$。
同时我们希望转换矩阵为整数，故令 $m'_n$的第2行和第4行×2,同时调整 $C_n$，则有最终的整数DCT变换：
$A'n=m'_n·A_n·m'^T_n\bigotimes Ef'$
其中
$m'_n= \begin{bmatrix} 1& 1& 1& 1\\ 2& 1& -1& 2\\ 1& -1& -1& 1\\ 1& -2& 2& -1\\ \end{bmatrix}\\ Ef'= \begin{bmatrix} a^2& \frac{ab}{2}& a^2& \frac{ab}{2}\\ \frac{ab}{2}& \frac{b^2}{4}& \frac{ab}{2}& \frac{b^2}{4}\\ a^2& \frac{ab}{2}& a^2& \frac{ab}{2}\\ \frac{ab}{2}& \frac{b^2}{4}& \frac{ab}{2}& \frac{b^2}{4}\\ \end{bmatrix}$

测试

$FDCT( \begin{bmatrix} 13& 34& 205& 255\\ 9& 43& 198& 254\\ 11& 35& 207& 254\\ 9& 36& 210& 237\\ \end{bmatrix} )= \begin{bmatrix} 502.500000& -403.842775& 18.500000& 89.886112\\ 4.493714& -4.553301& 9.337282& -6.906854\\ -3.000000& 3.444151& -4.000000& 8.314916\\ 3.009408& -4.406854& 4.250312& 6.053301\\ \end{bmatrix}\\ FDCT_{integer}( \begin{bmatrix} 13& 34& 205& 255\\ 9& 43& 198& 254\\ 11& 35& 207& 254\\ 9& 36& 210& 237\\ \end{bmatrix} )= \begin{bmatrix} 502.500000& -409.19873& 18.500000& 61.03196\\ 4.269075& -3.70000& 9.012491& -7.60000\\ -3.000000& 2.84605& -4.000000& 8.53815\\ 3.320392& -5.10000& 4.901530& 5.20000\\ \end{bmatrix}\\ FDCT-FDCT_{interger}= \begin{bmatrix} 0& 5.3559543& 0& 28.8541533\\ 0.2246392& -0.8533009& 0.324911& 0.6931458\\ 0& 0.5981010& 0& -0.2232339\\ -0.3109839& -0.6931458& -0.6512179& 0.8533009\\ \end{bmatrix}$
可以发现整数化的DCT与原DCT相差无几

备注

在h264中采用的是整数DCT变换，且将动作 $\bigotimes Ef'$放置到量化操作中