线段树概念&代码实现

概述

线段树是一种数据结构, 其采用了分块思想, 可解决RMQ, RSQ(Range sum query)问题, 同时优秀的将复杂度保持在O(log n)级别

相对比前缀和和ST表, 线段树支持修改

1. 线段树所用的变量定义&说明

在实现线段树时, 我一般习惯定义2个数组

int t[MAX << 2], a[MAX << 2];

其MAX请根据需求修改

t用来存储这棵树, 采用顺序标号的好处是可以快速的找到左右孩子

a用来存储原序列(即需要维护的序列), 在建树时有用

2. 减短代码量的一些函数定义&说明

上面提到, 采用顺序标号的好处是可以快速的找到左右孩子

即, 节点p的左孩子为p << 1(可理解为p * 2), 右孩子为p << 1 | 1(可理解为p * 2 + 1)

那么可以定义如下函数

inline int ls(int p) { return p << 1; }
inline int rs(int p) { return p << 1 | 1; }

ls用来查询左孩子, rs用来查询右孩子

3. 线段树思想&建树

在线段树中, 一个节点代表的并不是一个值, 而是一个区间的和/最大最小值/xor等等

接下来讨论的是区间的和

先来看一棵线段树

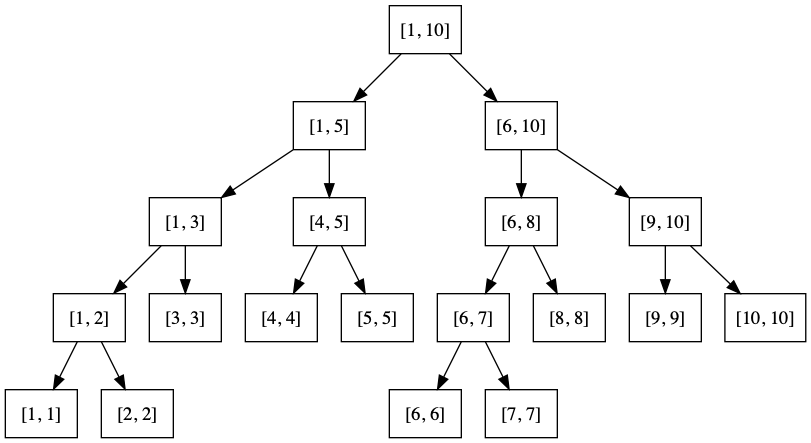
你会发现, 根节点维护的是[1, 10], 他的左孩子维护的是[1, 5], 右孩子是[6, 10]

根结点的左孩子的左孩子是[1, 3], 根结点的左孩子的右孩子是[4, 5]......

稍加思索便可得出: 如果一个节点维护的是[l, r]区间

那么他的左孩子维护的是[l, (l + r) / 2]区间, 右孩子维护的是[(l + r) / 2 + 1, r]区间

再来看叶子节点, 叶子节点维护的是一个仅有一个元素的区间, 如[1, 1]

在明白了这些之后, 我们来考虑建树

可以使用递归, 每次递归到叶子结点, 将叶子节点赋值, 在回溯

不过值得注意的是, 线段树维护的是一个区间的值, 一想便会发现一个非叶节点的值是他左孩子的值+右孩子的值

例如区间[1, 2], 它等于区间[1, 1] + 区间[2, 2]

再比如区间[1, 10], 它等于区间[1, 5] + 区间[6, 10]

那便可以写出维护父子关系的函数pushUp:

inline void pushUp(int p) {
    t[p] = t[ls(p)] + t[rs(p)];
}

再回过头来看build, 思路已经清晰了吧

build的三个参数p, l, r分别代表当前顺序标号存储的编号, l, r是维护的区间

inline void build(int p, int l, int r) {
    if(l == r) {
        t[p] = a[l];
    } else {
        int mid = (l + r) >> 1;
        build(ls(p), l, mid);
        build(rs(p), mid + 1, r);
        pushUp(p);
    }
}

3. 线段树的修改&Lazy tag

修改, 很明显可以暴力修改, 不过我相信看这篇文章80%的人都是OIer

所以我们来考虑一个问题: 一个区间的修改值不值得?

换句话说, 你修改了这个区间, 会不会来查询呢?

为了应对这种情况, 弄出了个叫做Lazy tag的东西, 不过这东西只能在维护和的时候使用

如果你使用线段树不是针对区间和, 请跳过这一段

Lazy tag用来存储修改操作, 然后在查询时将标记下传

先来看一下打标记:

int tag[MAX << 2];
inline void f(int p, int k, int l, int r) {
    t[p] += k * (r - l + 1), tag[p] += k;
}

其中, p, l, r意同build函数, k表示要修改的值

为什么t[p]要加上k * (r - l + 1)呢? 大家应该都知道(r - l + 1)表示的是区间元素个数...

是的, 只是将它所有孩子要修改的值暂存在它那里

而tag[p]加上k是记录这一个节点记录了一次值为k的修改

接下来是下传函数

inline void pushDown(int p, int l, int r) {
    int mid = (l + r) >> 1;
    f(ls(p), tag[p], l, mid);
    f(rs(p), tag[p], mid + 1, r);
    tag[p] = 0;
}

p, l, r意同build函数, 就是将左右孩子打上标记, 最后清零自己

最后是update函数:

inline void update(int nl, int nr, int l, int r, int p, int k) {
    if(nl <= l && r <= nr) {
        t[p] += k * (r - l + 1), tag[p] += k;
    } else {
        int mid = (l + r) >> 1;
        pushDown(p, l, r);
        if(mid >= nl) update(nl, nr, l, mid, ls(p), k);
        if(mid < nr) update(nl, nr, mid + 1, r, rs(p), k);
        pushUp(p);
    }
}

nl, nr是指要更新的区间, l, r, p意同build, k是修改的值

第一句if(nl <= l && r <= nr)是指如果在待修改区间内, 就打上标记

在当时我学的时候, if(mid < nr)这一句让我感到很迷, 上面都是mid >= nl, 怎么这里就 < nr了, 不应该是 <= nr?

你看下面mid + 1, 万一它等于nr然后再加一, 不就超出了指定范围吗?

4. 查询操作

先放上代码, 我觉得到这里应该也没什么要说的了:

inline int query(int nl, int nr, int l, int r, int p) {
    if(nl <= l && r <= nr) return t[p];
    int mid = (l + r) >> 1, res = 0;
    pushDown(p, l, r);
    if(mid >= nl) res += query(nl, nr, l, mid, ls(p));
    if(mid < nr) res += query(nl, nr, mid + 1, r, rs(p));
    return res;
}

nl, nr, l, r, p意同update函数

在我学的时候, if(nl >= l && r <= nr)这一句不太理解, 其实你想, 如果l, r在要查询的区间里, 肯定也是答案的一份子, 直接返回就可以了嘛

那么, 到这里也差不多了?

5. 其他操作

如果你想要用线段树来做RMQ或其他什么的

先牢记一点: 线段树只能维护父子节点关系唯一且确定的操作

那如何做到呢? 只需要修改pushUp函数:

RMQ的pushUp:

inline void pushUp(int p) {
    t[p] = max(t[ls(p)], t[rs(p)]);
    //t[p] = min(t[ls(p)], t[rs(p)]);
}

区间XOR的pushUp:

inline void pushUp(int p) {
    t[p] = t[ls(p)] ^ t[rs(p)];
}

.......

6. 样例题目: LuoguP3372

就是一道线段树裸题嘛, 不过记得开long long

#include<stdio.h>
#define MAX 1000005
typedef long long ll;

ll t[MAX << 2], a[MAX << 2], tag[MAX << 2];
inline int ls(int p) { return p << 1; }
inline int rs(int p) { return p << 1 | 1; }
inline void pushUp(int p) {
    t[p] = t[ls(p)] + t[rs(p)];
}
inline void build(int p, int l, int r) {
    if(l == r) {
        t[p] = a[l];
    } else {
        int mid = (l + r) >> 1;
        build(ls(p), l, mid);
        build(rs(p), mid + 1, r);
        pushUp(p);
    }
}
inline void f(int p, int k, int l, int r) {
    t[p] += k * (r - l + 1), tag[p] += k;
}
inline void pushDown(int p, int l, int r) {
    int mid = (l + r) >> 1;
    f(ls(p), tag[p], l, mid);
    f(rs(p), tag[p], mid + 1, r);
    tag[p] = 0;
}
inline void update(int nl, int nr, int l, int r, int p, int k) {
    if(nl <= l && r <= nr) {
        t[p] += k * (r - l + 1), tag[p] += k;
    } else {
        int mid = (l + r) >> 1;
        pushDown(p, l, r);
        if(mid >= nl) update(nl, nr, l, mid, ls(p), k);
        if(mid < nr) update(nl, nr, mid + 1, r, rs(p), k);
        pushUp(p);
    }
}
inline ll query(int nl, int nr, int l, int r, int p) {
    if(nl <= l && r <= nr) return t[p];
    ll mid = (l + r) >> 1, res = 0;
    pushDown(p, l, r);
    if(mid >= nl) res += query(nl, nr, l, mid, ls(p));
    if(mid < nr) res += query(nl, nr, mid + 1, r, rs(p));
    return res;
}
int main(int argc, char** args) {
    int n = 0, m = 0;
    scanf("%d %d", &n, &m);
    for(int i = 1;i <= n;i++) {
        scanf("%lld", &a[i]);
    }
    build(1, 1, n);
    int ta = 0, tb = 0, tc = 0, td = 0;
    for(int i = 0;i < m;i++) {
        scanf("%d %d %d", &ta, &tb, &tc);
        if(ta == 1) {
            scanf("%d", &td);
            update(tb, tc, 1, n, 1, td);
        } else {
            printf("%lld\n", query(tb, tc, 1, n, 1));
        }
    }
}

那么, 到此为止了