抽屉原理（鸽巢原理）

直观描述

桌上有十个苹果，要把这十个苹果放到九个抽屉里，无论怎样放，至少会有一个抽屉里面至少放两个苹果。
如果有五个鸽子笼，养鸽人养了6只鸽子，那么当鸽子飞回笼中后，至少有一个笼子中装有2只鸽子。
抽屉原理有时也被称为鸽巢原理。它是组合数学中一个重要的原理。

内容

1.有至少n+1个物体，分为n组，至少有一组有两件以上。
证明（反证法）：如果每组至多只有一个物体，那么物体的总数至多是n，无法容纳n+1个物体，矛盾。

2.有至少 $m*n+1$个物体，分为n组，至少有一组有m+1件或以上。
证明（反证法）：若每组最多有m个物体，则物体总数是 $m*n$，无法容纳 $m* n+1$件物体，矛盾。

一些表现形式

1.从 1,2,··· ,2n 中选出 n + 1 个整数，一定存在一个数是另一个数的因子。
2.从 1,2,··· ,2n 中选出 n + 1 个整数，一定存在两个数互质。
3.在边长为 n 的等边三角形内选出 5 个点，一定存在一个点到另一个点距离不超过 n/2。
4.任意7个整数中，至少有3个数的两两之差是3的倍数。

Ramsey定理与Ramsey数

通俗表述

任意6个人中至少存在3人相互认识或者相互不认识。

证明

假设6个人是6个点，如果两人认识则连一条红线，不认识则连一条蓝线，原问题转化为：必然存在一个三角形三边同色。

1. 对任意一个点A，其他五个点与A有两种线可连（红、蓝），由抽屉原理知，必然有一种颜色的线连了至少三个点，不妨设红线连接了它们，被连接的点分别记为B,C,D。（另外两个点可以连红线也可以连蓝线）

接下来对BCD这个三角形进行讨论：

2. 如果存在一条红线，则这条线必然与刚刚三条红线中的两条形成一个红色三角形。
3. 如果不存在红线，即三条均为蓝线，则存在BCD这个蓝色三角形。

此过程可以参考下图。

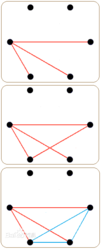
一般表述

在一个有n个点的图中，用红蓝两种颜色进行着色，无论何种情况必至少存在以下两者之一：(1)一个a个顶点着红颜色的完全子图，或一个b个顶点着蓝颜色的完全子图；(2)一个a个顶点着蓝颜色的完全子图，或一个b个顶点着红颜色的完全子图。最小的满足条件的n即为R(a,b)。
也就是说，R(a,b)的值为满足以下四种条件之一的最小人数n：

1. a个人两两认识
2. a个人两两不认识
3. b个人两两认识
4. b个人两两不认识

Ramsey证明，对于给定的正整数k及l，R(k,l)的答案是唯一和有限的。

R(3,3)=6

我们刚刚证明的结果可表述为R(3,3)<=6，因为R(a,b)代表满足条件的最小值，所以不仅要找到满足条件的值n，还要找到一种不满足条件的方案。
下图就是一个5个点不满足条件的涂色方案：

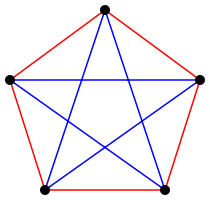
只要有一种无法满足的方案存在，这个n就小于R(a,b)，故R(3,3)>5。
因此，5<R(3,3)<=6，即R(3,3)=6。

其他的Ramsey数

虽然R(3,3)的证明十分巧妙，但是实际上已知的Ramsey数非常少，保罗·艾狄胥曾以一个故事来描述寻找拉姆齐数的难度：
“想像有队外星人军队在地球降落，要求取得R(5,5)的值，否则便会毁灭地球。在这个情况，我们应该集中所有电脑和数学家尝试去找这个数值。若它们要求的是R(6,6)的值，我们要尝试毁灭这班外星人了。”
下图是Ramsey数的表格¹。因为R(r,s)=R(s,r)，所以只给出了上三角形。

其中，绿色格子代表已经确定的Ramsey数，而带有范围的黄色格子表示尚未确定，如R(5,5)在43和48之间，这说明R(5,5)>42且R(5,5)<=48，即存在至少一种方案给42个点涂色使全部条件均不满足，且任意涂色方案给48个点涂色均满足至少一个条件，但对于43~47中的数暂不确定条件是否满足。

目前我们只需要了解 R(1,m) = 1, R(2,m) = m, R(3,3) = 6,R(4,4) = 18即可。