首先给出定义如下：

我们考虑n维特征存在冗余，需要降低样本维度。一个样本由n维特征表示，即由n个数字表示。就相当于在2维空间中用一个坐标（m,n）去表示一个向量，如果对很多很多样本（这些样本就是坐标）进行降维，我们会考虑将其投影到一条直线上，投影在这条直线的点就是对于这些向量新的表示，如下所示：

更抽象来说就是寻找一个新的基去表示向量，现在的问题转化为怎么寻找合适的基以达到降维的效果。由于基的个数就决定了被表示的向量的维度，所以：1、新的基的个数需要远小于原始样本的维度（即特征个数）。其次，在图二中有很多种投影方式，例如投影到x轴或者y轴。

但是，这些投影方式会使得部分点重叠，也就是会损失部分样本信息，说明这样的基的选择不合适。所以：2、我们考虑将样本投影到新的基后能获得最大化的方差（样本尽量分散的开）以保证其信息的较少损失。（PS：为了便于后续计算，我们首先对数据进行0均值处理）

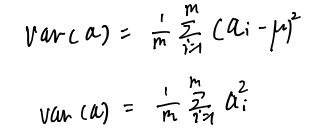
进一步，需要考虑更高维的情况，所以仅仅考虑投影到一个基上的最大化方差的标准是不充分的。因为只考虑方差最大化，其他的基会与最大化方差的基重合，这样就相当于只用1维特征去表示样本，很明显损失的是不同字段的信息表达能力。所以：3、我们要考虑新的基组（字段）能尽量衡量样本的不同方面特性，即基之间的相关性最低。数学上的相关性量化是通过向量的协方差建立，所以新的基要使得不同字段间的协方差为0。

下面的主要工作就是在协方差为0的基础上最大化方差。我们首先写出a，b两个字段的数据表示如下：

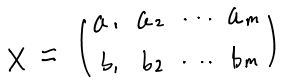
我们发现如下表示：（C为原始数据X的协方差矩阵）

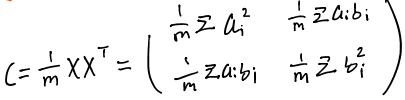
我们现在寻找到新的基P来表示X成Y，则有：

对于新基下Y的协方差矩阵D有：

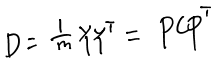
由于D为实对称矩阵（同C），所以对D的对角化（对角化会使得Y的协方差为0，主对角线上是特征值）转化为求E（E就是特征向量矩阵），而这个E的转置正好也是所要求的新基P：

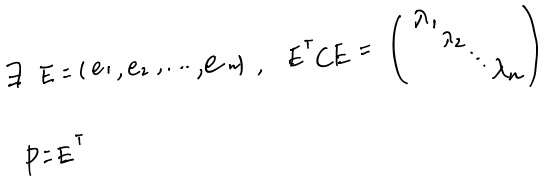
最后，由于原始数据是n维的，我们考虑用P将其表示成k维（k远小于n），只要选用前k个特征值对应的特征向量组成的矩阵作为P就可以了。
【初步理解-2019.2.25】