从 机器学习面试必知：SVM和LR的关系 一文中,我们可以看到SVM相比于LR的优势在于能产生稀疏解。现在把SVM应用到回归问题中，同时保持它的稀疏性。在简单的线性回归模型中，我们最小化一个正则化的误差函数 $\frac{1}{2}\sum_{n=1}^{N}(y_{n}-t_{n})^{2}+\frac{\lambda}{2}||w||^{2}$为了得到稀疏解，二次误差函数被替换成一个 $\epsilon$不敏感误差函数。如果预测 $y(x)$与目标 $t$之间的差的绝对值小于 $\epsilon$，那么这个误差函数给出的误差为0。 $E_{\epsilon }(y(x)-t)= \left\{\begin{matrix} 0,\quad \quad if \ \ |y(x)-t|<\epsilon\\ |y(x)-t|<\epsilon,\ otherwise \end{matrix}\right.$于是我们最小正则化的误差函数 $C\sum_{n=1}^{N} E_{\epsilon }(y(x_{n})-t_{n})+\frac{1}{2}||w||^{2}$为了有更好的泛化能力，我们引入松弛变量 $\xi_{n}\geq0$和 $\widetilde{\xi_{n}}\geq0$分别代表上界和下界。

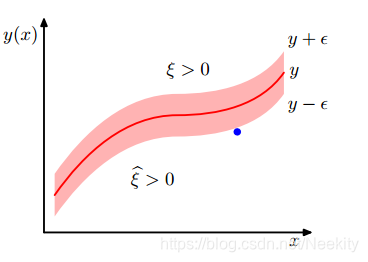
从图中可以看到， $\xi_{n}>0$对应的是 $t_{n}>y(x_{n})+\epsilon$数据点， $\widetilde{\xi_{n}}>0$对应的是 $t_{n}<y(x_{n})-\epsilon$数据点，所以 $t_{n}\leq y(x_{n})+\epsilon+\xi_{n}$ $t_{n}\geq y(x_{n})-\epsilon-\widetilde{\xi_{n}}$相应地支持向量回归的误差函数可以写成 $C\sum_{n=1}^{N}(\xi_{n}+\widetilde{\xi_{n}})+\frac{1}{2}||w||^{2}$我们引入拉格朗日乘数 $a_{n}\geq0$， $\widetilde{a_{n}}\geq0$， $u_{n}\geq0$和 $\widetilde{u_{n}}\geq0$，然后最优化拉格朗日函数 $L=C\sum_{n=1}^{N}(\xi_{n}+\widetilde{\xi_{n}})+\frac{1}{2}||w||^{2}-\sum_{n=1}^{N}u_{n}\xi_{n}-\sum_{n=1}^{N}\widetilde{u_{n}}\widetilde{\xi_{n}}-\sum_{n=1}^{N}a_{n}(y(x_{n})+\epsilon+\xi_{n}-t_{n})-\sum_{n=1}^{N}\widetilde{a_{n}}(-y(x_{n})+\epsilon+\widetilde{\xi_{n}}+t_{n})$ $\frac{\partial L}{\partial w}=0\Rightarrow w=\sum_{n=1}^{N}(a_{n}-\widetilde{a_{n}})\phi(x_{n})$ $\frac{\partial L}{\partial b}=0\Rightarrow 0=\sum_{n=1}^{N}(a_{n}-\widetilde{a_{n}})$ $\frac{\partial L}{\partial \xi_{n}}=0\Rightarrow a_{n}+u_{n}=C$ $\frac{\partial L}{\partial \widetilde{\xi_{n}}}=0\Rightarrow \widetilde{a_{n}}+\widetilde{u_{n}}=C$把这些结果代入到L中得到 $\widetilde{L}(a,\widetilde{a})=-\frac{1}{2}\sum_{n=1}^{N}\sum_{m=1}^{N}(a_{n}-\widetilde{a_{n}})(a_{m}-\widetilde{a_{m}})K(x_{n},x_{m})-\epsilon\sum_{n=1}^{N}(a_{n}+\widetilde{a_{n}})+\sum_{n=1}^{N}(a_{n}-\widetilde{a_{n}})t_{n}$同样地我们得到了限制条件 $0\leq a_{n}\leq C$ $0\leq \widetilde{a_{n}}\leq C$对应的KKT条件等于零的情况如下 $a_{n}(y(x_{n})+\epsilon+\xi_{n}-t_{n})=0$ $\widetilde{a_{n}}(-y(x_{n})+\epsilon+\widetilde{\xi_{n}}+t_{n})=0$ $(C-a_{n})\xi_{n}=0$ $(C-\widetilde{a_{n}})\widetilde{\xi_{n}}=0$分析上述的等式我们可以得到些有用的结果。如果 $y(x_{n})+\epsilon+\xi_{n}-t_{n}=0$,那么 $a_{n}\neq0$，进一步的，如果 $a_{n}=C$也就是 $\xi_{n}>0$此时数据点位于上边界的上方，如果 $\xi_{n}=0$那么数据点位于管道的上边界上。同理可以分析 $-y(x_{n})+\epsilon+\widetilde{\xi_{n}}+t_{n}=0$。
我们已经得到了 $y(x)=\sum_{n=1}^{N}(a_{n}-\widetilde{a_{n}})K(x_{n},x)+b$现在寻找支持向量也就是有贡献的数据点即 $a_{n}\neq0$或者 $\widetilde{a_{n}}\neq0$的点。这些数据点位于管道边界上或者管道外部，管道内部的点有 $a_{n}=\widetilde{a_{n}}=0$。更一般地，我们使用前文的分析用满足 $0<a_{n}<C$,此时 $\xi_{n}=0$, $y(x_{n})+b+\epsilon+\xi_{n}-t_{n}=0$,那么 $b=-w^{T}\phi(x_{n})-\epsilon+t_{n}$或者用 $0<\widetilde{a_{n}}<C$的数据点去求解b。当然更好的方法对所有符合条件的情况取平均。