最近正在研究高数上的微积分一章, 目的是为了以后做机器学习和深度学习做准备, 但是2年没碰数学的我似乎连一些高中数学的问题都搞不定了, 于是选择了一个挑战任务: 证明切割线定理, 但是不同的是, 我试图不依赖其他的定理来证明它, 因此整个流程是这样的: 首先要证明切割线定理就要证明弦切角定理, 然后证明弦切角又需要二倍角(圆周角)定理的支持, 证明二倍角只需要知道三角形内角和等于180°, 那如何证明△内角和是180°呢, 我发现了一些神奇的现象!

如何证明切割线定理

切割线定理(Tangent-secant theorem) 指的是圆外关键一点P, 从P引出切线和割线, 然后集合图中出现了经过P的3个线段, 线段之间满足等比关系.

只要利用相似三角形和弦切角定理就能证明

相似三角形原理不用证明, 因为一眼就能看出来, 没有'玄学'的感觉[强迫症]

如何证明弦切角-圆周角定理呢?

弦切角是圆上一点引出的一条切线和弦(或者割线), 2条线的夹角,

而弦切角正好等于刚刚的弦对应的圆周角.

如何证明呢, 只要把圆心和几个点连一下, 根据圆心角等于2倍圆周角即可轻松证明. 过程略

可是我证到这儿还是TM不满意啊, 因为圆周角定理还是很玄乎哇, 不舒服!

证明圆周角等于圆心角一半!(太无聊了)

还是只要把圆心一连接就可以了, 我已经不想证明了, 因为和证明弦切角定理相比, 这次证明并没有实质性突破, 而且都用到了三角形内角和定理, 而且三角形内角和也非常好证明, 只要画一条平行线就行了:

可以看到, 最后的证明只用到了一个规则: 一个水平的角等于π(180°), 也就是图中l上的A点. 当然, 我们不需要证明一条直线上任意一点的角度等于π, 因为这只是一个标识. 所以到目前为止刨根问底式证明切割线定理完成了, 但总是感觉不满意, 不知道为什么总感觉这个三角形很奇怪, 为什么三角形稳定? 为什么这么简单的三角形不能一眼看出内角和是π?. 其实:

证明内角和没有意义, 外角和才有意义

多边形内角和公式是(n-2)*π, 但外角和永远是2*π, 让我感觉外角和才是真正问题的关键! 如何证明外角和是2*π?事实上内角和公式是由外角和推导出来的. 有一种直观的极限几何解是我最喜欢的解法:

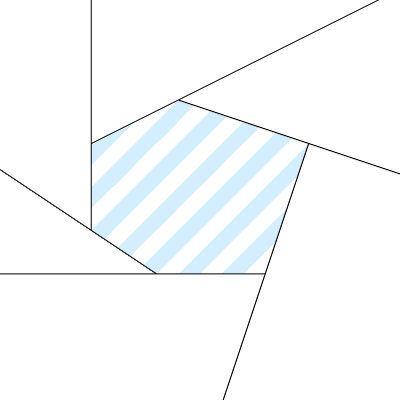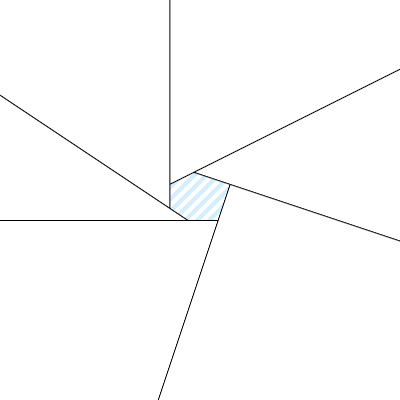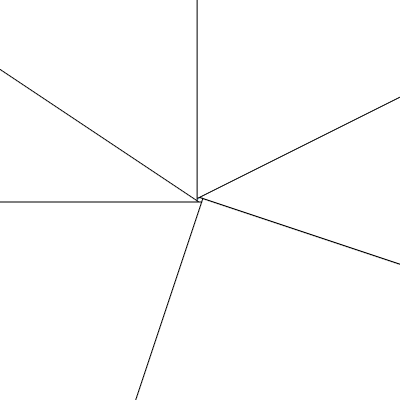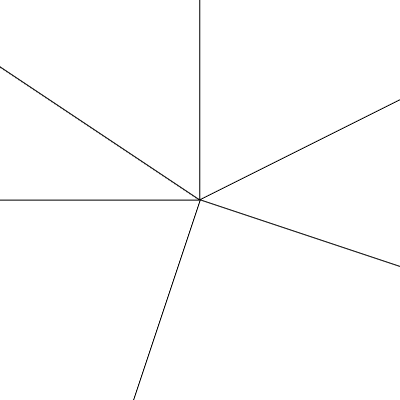
这个动图中, 当视角无限放大, 中间的多边形变成了一个点, 所有的外角正好围成了一周, 

试图在降维打击中找到线索...

上面通过极限积分的方式将多边形面降成了一个点, 正是一个降维的思想, 也可以用向量来表示多边形,  比如三角形, 可以看成是一条路径, 向量从起点A出发, 经由B, C回到A, 每次转弯旋转的角度就是一个外角, 旋转一周正好是2*π, 所以说, 三角形不过是一维向量运动得到的一个二维错觉, 虚拟的高维度几何都可以序列化成低维度的线性集合, 这就是向量的本质, 通过运动来实现虚拟化.

 所以说, 想了解几何学的本质还是的通过降维的思想.

其实这篇文章写得很烂, 大部分都是主观意识下瞎猜的, 如果觉得有不合理的地方就以你自己的认知为主吧.