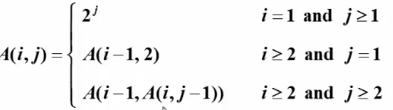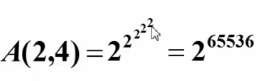3.树之堆、哈夫曼树以及集合

其他 2019-04-20 17:50:52 阅读次数: 0

（一）堆的定义

优先队列（priority queue）：特殊的“队列”，却出元素的顺序是依照元素的优先权（关键字）大小，而不是元素进入队列的先后顺序。

若采用数组或者链表实现优先队列：

  1. 数组
    插入：元素总是插入尾部 ~O(1)
    删除：查找最大（最小）关键字 ~O(n)
    ———从数组中删除元素并移动~O(n)

  2. 链表
    插入：元素总是插入链表的头部~O(1)
    删除：查找最大（最小）关键字 ~O(n)
    ————删去结点 ~O(1)

  3. 有序数组
    插入：找到合适的位置~O(n)或O(log2n)
    ————移动元素并且插入~O(n)
    删除：删去最后一个元素~O(1)

  4. 有序链表
    插入：找到合适的位置~O(n)
    ———插入元素~O(1)
    删除：删除首元素或者最后元素~O(1)

是否可以采用二叉树存储结构？

  • 二叉搜索树：每次删除最大的，意味着每次都删除右子树，那么树就不平衡了。
  • 如果采用二叉树结构，应该更关注插入还是删除？
    树的结点顺序怎么安排？ 最大的/最小的保存在树根
    树结构怎么样？完全二叉树

堆的两个特性

  • 结构性：用数组表示的完全二叉树
  • 有序性：任意结点的关键字是其子树所有结点的最大值（或最小值）
    最大堆：大堆顶
    最小堆：小顶堆
    在这里插入图片描述
    最大堆和最小堆每一条路径都满足：从大到小或从小到大，且都是完全二叉树
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

（二）最大堆的建立

  • 方法1：通过插入操作，将N个元素一个个相机插入到一个促使为空的堆中去，其时间代价最大为O(NlogN)
  • 方法2：在线性时间复杂度下建立最大堆
    (1)将N个元素按输入顺序存入，先满足完全二叉树的结构特性
    (2)调整各结点的位置，以满足最大堆的有序特性
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    **建堆时，最坏情况下需要挪动元素次数是等于树中各结点的高度和。**问：对于元素个数为12的堆，其各结点的高度之和是多少？
    1
    2 3
    4 5 6 7
    8 9 10 11 12
    建堆的话，主要考虑下沉的次数，以此定义高度。8,9,10,11,12都是已经沉底的，要注意的是7也是在最底了。这些节点高度都是0。
    4,5,6都是最多可以沉1次的，高度为1.
    2,3最多能沉2次，高度为2.
    1可以沉3次，高度为3.
    1*3+2*2+3*1=3+4+3=10

05-树7 堆中的路径 （25 分)
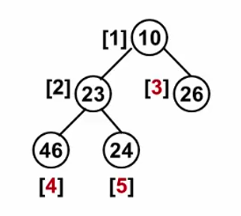
将一系列给定数字插入一个初始为空的小顶堆H[]。随后对任意给定的下标i，打印从H[i]到根结点的路径。
输入格式:
每组测试第1行包含2个正整数N和M(≤1000)，分别是插入元素的个数、以及需要打印的路径条数。下一行给出区间[-10000, 10000]内的N个要被插入一个初始为空的小顶堆的整数。最后一行给出M个下标。
输出格式:
对输入中给出的每个下标i，在一行中输出从H[i]到根结点的路径上的数据。数字间以1个空格分隔，行末不得有多余空格。

输入样例:
5 3
46 23 26 24 10
5 4 3
输出样例:
24 23 10
46 23 10
26 10

题意理解：在这里插入图片描述

#include <vector>
#include <stdio.h>
#include <iostream>
using namespace std;

//05-树7 堆中的路径 （25 分)
#define MAXN 1001
#define MINH -10001
int heap[MAXN];
int h_size;

//建立一个空堆
void Create()
{
	h_size = 0;
	heap[0] = MINH;		 /*设置“岗哨”*/
}

//最小堆的插入，方法是从最后一个结点开始比较
void Insert(int X)
{
	//省略判断堆是否已满
	int i;
	for (i = ++h_size; heap[i / 2] > X; i /= 2){
		heap[i] = heap[i / 2];	
		//将父结点放到下一级即其儿子结点，直到插入的值小于某个子树的根节点
	}
	heap[i] = X;
}

int main()
{
	int n, m, x, i, j;
	cin >> n >> m;
	Create();
	for (i = 0; i < n; ++i)
	{
		cin >> x;
		Insert(x);
	}
	//输出路径
	for (i = 0; i < m; i++)
	{
		cin >> j;
		cout << heap[j];
		while (j > 1)
		{
			j /= 2;
			cout << " " << heap[j];
		}
		cout << endl;
	}
	return 0;
}

（三）哈夫曼树与哈夫曼编码

  1. 什么是哈夫曼树？
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

如何根据节点不同的查找频率构造更有效的搜索树？

  1. 哈夫曼树的定义
    带权路径长度（WPL）：设二叉树有n个叶子结点，每个叶子结点带有权值Wk，从根节点到每个叶子结点的长度为lk，则每个叶子结点的带全路径长度之和就是：WPL=∑nk=1(wklk)
    最优二叉树或哈夫曼树：WPL最小的二叉树
    在这里插入图片描述
  2. 哈夫曼树的构造
    每次把权值最小的两棵二叉树合并
    时间复杂度不超过O(nlogn)
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
  3. 哈夫曼树的特点
    （1）没有度为1的结点；
    （2）n个叶子结点的哈夫曼树共有2n-1个结点；
    n0：叶结点总数
    n1：只有一个儿子的结点总数
    n2：有2个儿子的结点总数
    n2=n0-1
    （3）哈夫曼树的任意非叶结点的左右子树交换后仍是哈夫曼树；
    （4）对于同一组权值{w1，w2，…，wn}，是否存在不同构的两棵哈夫曼树呢？
    最优化的值是一样的

如果哈夫曼树有67个结点，则可知叶结点总数为：2n0-1=67 n0=34在这里插入图片描述

（四）哈夫曼编码

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

字符都在叶子结点上，若出现在某个子数的根结点上，就会出现二义性
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

怎么构造一棵编码代价最小的二叉树？
哈夫曼树！

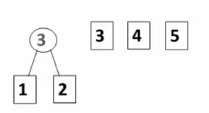
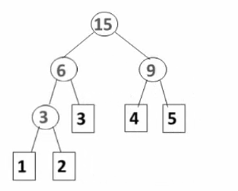
在这里插入图片描述
一段文本中包含对象{a,b,c,d,e}，其出现次数相应为{3,2,4,2,1}，则经过哈夫曼编码后，该文本所占总位数为：
A.12 B.27
C.36 D.其它都不是
正确答案：B
在这里插入图片描述
在这里插入图片描述

（五）集合

  • 集合运算：交、并、补、差、判定一个元素是否属于某一集合
  • 并查集合：集合并、查某元素属于什么集合
  • 并查集问题中的集合存储如何实现
    a）可以用树结构表示集合，树的每个结点表示一个集合元素
    b）采用数组存储形式
    在这里插入图片描述
    在这里插入图片描述
  • 集合的并运算
    （1）分别找到X1和X2两个元素所在集合树的根结点。
    （2）如果他们不同根，则将其中一个根结点的父结点指针设置为另外一个根结点的数组下标。
    为了改善合并以后的查找性能，可以采用小的集合合并到相对大的集合中。
    在这里插入图片描述
    已知a、b两个元素均是所在集合的根结点，且分别位于数组分量3和2位置上，其parent值分别为-3,-2。问：将这两个集合按集合大小合并后，a和b的parent值分别是多少？
    A.-5，2 B.-5，3
    C.-3，3 D.2，-2
    正确答案：B

05-树8 File Transfer （25 分)
We have a network of computers and a list of bi-directional connections. Each of these connections allows a file transfer from one computer to another. Is it possible to send a file from any computer on the network to any other?
Input Specification:

Each input file contains one test case. For each test case, the first line contains N (2≤N≤10
​4
​​ ), the total number of computers in a network. Each computer in the network is then represented by a positive integer between 1 and N. Then in the following lines, the input is given in the format:
I c1 c2
where I stands for inputting a connection between c1 and c2; or
C c1 c2
where C stands for checking if it is possible to transfer files between c1 and c2; or
S
where S stands for stopping this case.
Output Specification:

For each C case, print in one line the word “yes” or “no” if it is possible or impossible to transfer files between c1 and c2, respectively. At the end of each case, print in one line “The network is connected.” if there is a path between any pair of computers; or “There are k components.” where k is the number of connected components in this network.

Sample Input 1:
5
C 3 2
I 3 2
C 1 5
I 4 5
I 2 4
C 3 5
S
Sample Output 1:
no
no
yes
There are 2 components.

Sample Input 2:
5
C 3 2
I 3 2
C 1 5
I 4 5
I 2 4
C 3 5
I 1 3
C 1 5
S
Sample Output 2:
no
no
yes
yes
The network is connected.

解题思路：
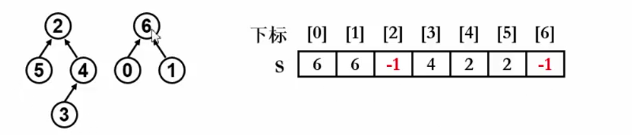
集合的简化表示：
在这里插入图片描述

  1. 在第2个步骤内，找到该元素在集合内的位置，然后再根据该元素的位置往上找，直到找到某个元素的父结点为-1，那么就是该元素的根结点了。
  2. 找->线性扫描，最坏的情况是该元素为第n个（即最后一个），如果找n次这个元素，那么总体的时间复杂度就是O(n2)。这是否有必要呢？
  3. 在本题内，计算机的编号从1到n编号的，也就是说Data是整数。

任何有限集合的（N个）元素都可以背一一映射为整数0~N-1
那么计算机1~n映射成0~n-1，即集合内的元素的值可以直接用其下标的值代替，数据域可以舍弃。
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

按秩归并

在这里插入图片描述
T(n)=Q(n2)！
在这里插入图片描述
在这里插入图片描述
最坏情况下的树高=O(logn)
即两棵一样高的树归并，每次树高加1

路径压缩

在这里插入图片描述
好处：虽然调用一次比较麻烦，但是从此以后如果还需要find其他结点的话，就会变得非常合算。
注意：Find函数其实是一个伪递归，真递归若结点太多堆栈太多会爆掉，伪递归很容易变成循环，编译器会帮助我们直接完成转化，执行优化后的循环。

时间复杂度：
在这里插入图片描述
意思是：
最坏情况的复杂度是：k2Mα(M，N)
最好情况的复杂度是：k1Mα(M，N)
α(M，N)与Ackermann函数有关
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
因此α(M，N)函数不是一个常数，随着M与N趋于无穷大而慢慢趋于无穷大，一般不超过4。

做路径压缩和不做路径压缩的区别是：乘以logn还是乘以α(M，N)（近似一个常数）

#include <vector>
#include <stdio.h>
#include <iostream>
using namespace std;
//05-树8 File Transfer （25 分)


typedef int ElementType;	 //默认元素可以用非负整数表示
typedef int SetName;//默认用根结点的下标作为集合名称
typedef ElementType SetType[10001];

//查找某个元素的位置 ，X即为下标也为目标值
//S[X]为父结点的下标值
SetName Find(SetType S, ElementType X)
{
	if (S[X] < 0)
		return X;
	else
		return S[X] = Find(S, S[X]);		
	//先找到根；把根变成X的父结点；在返回根；
}

void Initialization(SetType S, int n)
{
	for (int i = 0; i < n; i++) S[i] = -1;
}

//把小树贴在大树上	 S[Root]=-元素个数
void Union(SetType S, SetName Root1, SetName Root2)
{
	if (S[Root1] < S[Root2]) {
		S[Root2] += S[Root1];
		S[Root1] = Root2;
	}
	else{
		S[Root1] += S[Root2];
		S[Root2] = Root1;
	}
}
//输入计算机连接
void Input_connection(SetType S)
{
	ElementType u, v;
	SetName Root1, Root2;
	cin >> u >> v;
	Root1 = Find(S, u - 1);//映射 1~n映射到0~n-1
	Root2 = Find(S, v - 1);
	if (Root1 != Root2);
		Union(S, Root1, Root2);
}

 //查询计算机连接
void Check_connection(SetType S)
{
	ElementType u, v;
	SetName Root1, Root2;
	cin >> u >> v;
	Root1 = Find(S, u - 1);//映射 1~n映射到0~n-1
	Root2 = Find(S, v - 1);
	if (Root1 == Root2)
		cout << "yes" << endl;
	else
		cout << "no" << endl;
}

 //计算网络连接个数
void Check_network(SetType S, int n)
{
	int i, counter = 0;
	for (i = 0; i < n; i++)
	{
		if (S[i] < 0)
			counter++;
	}
	if (counter == 1)
		cout << "The network is connected.";
	else {
		cout << "There are " << counter << " components.";
	}
}

int main()
{
	SetType S;
	int n;
	char in;
	cin >> n;
	Initialization(S, n);
	do {
		cin >> in;
		switch (in)
		{
		case 'I':
			Input_connection(S);
			break;
		case 'C':
			Check_connection(S);
			break;
		case 'S':
			Check_network(S,n);
			break;
		}
	} while (in != 'S');
	return 0;
}

猜你喜欢

转载自blog.csdn.net/CarmenIsOK/article/details/88907231
今日推荐
周排行
成为C++高手之宏与枚举
在CAD二次开发中使用进度条
Js插件ECharts，HighCharts学习网址整理
Celery提交任务出错(on windows.)
cephfs内核客户端性能追踪
thinkphp中PHPExcel用法
EntityFramework动态组合多排序字段
汇编语言（八）实验9 根据材料编程
安装ubuntu后必须做的事情（对我而言）
JS函数式编程
每日归档
更多
2024-10-22(0)
2024-10-21(0)
2024-10-20(0)
2024-10-19(0)
2024-10-18(0)
2024-10-17(0)
2024-10-16(0)
2024-10-15(0)
2024-10-14(0)
2024-10-13(0)

代码天地 © 2018 codetd.com

境外服务器   最新电视剧2022