版权声明:本文为博主原创文章,未经博主允许不得转载。 https://blog.csdn.net/yanchuan23/article/details/89519160
1.平面向量
1.1平面向量的加法运算
两个向量,
;
向量满足四边形法则;

1.2平面向量的乘法运算
两个向量,
;
向量乘表示为
;
相比于向量加运算,向量乘运算要复杂点,很难看明白向量乘的几何意义;
将和
用极坐标表示:
则向量乘法表示为:

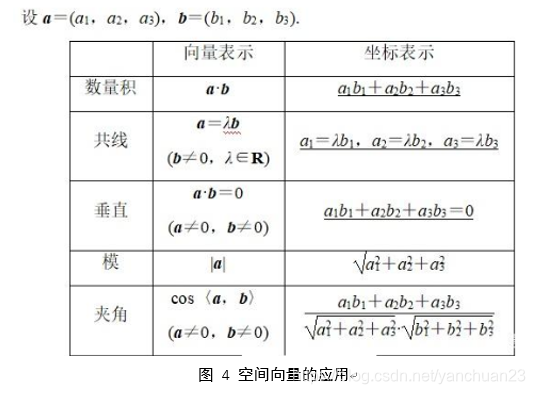
2.空间向量
如果三个向量、
、
不共面,那么对空间任一向量
,存在唯一的有序实数组
,使的
。
模长;