反转（开关问题）

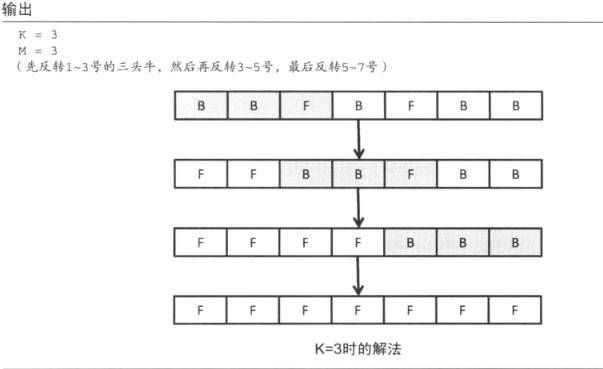
　　对于一个特定的 K 如何求出让所有牛面朝前方的最小操作数。如果把牛的方向作为状态进行搜索的话，由于状态数有 2^N 个，是无法在时限内得出答案的。

　　首先，交换区间反转的顺序对结果是没有影响的。此外，对同一区间进行两次以上的反转是多余的。由此，问题就转化成了求需要被反转区间的集合。先考虑一下最左端的牛。包含这头牛的区间就只有一个，因此如果这头牛面朝前方，我们就能知道这个区间不需要反转。

　　反之，如果这头牛朝后方，对应的区间就必须反转。而且在此之后这个最左的区间就不需要考虑了。不断重复下去，就可以无需搜索求出最少需要的反转次数。

　　通过上面的分析可以知道，忽略掉对同一区间重复反转这类多余操作之后，只要存在让所有牛都朝前的方法，那么操作就和顺序无关可以唯一确定了。

　　这个算法的复杂度：首先需要对所有的 K 都求解一次，对于每个 K 都要从最左端开始来考虑 N 头牛的情况。此时最坏的情况下需要进行 N - K + 1 次的反转操作，而每次操作又要反转 K 头牛，于是总的复杂度为 O（N³）。这样还是不行，还需要对区间反转的部分进行优化。

　　f [ i ] := 区间 [ i, i + K - 1 ]进行了反转的话则为1，否则为0

　　这样，在考虑第 i 头牛时，如果为奇数的话，则这头牛的方向与起始反向是相反的，否则方向不变。由于

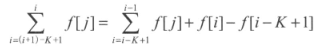
　　所以这个和每一次都可以用常数时间计算出来，复杂度降为 O（N²）

int N;
int dir[MAX_N]; // 牛的方向（0：F， 1：B） 
int f[MAX_N];     // 区间[i, i + K - 1]是否进行反转

//固定K，求对应的最小操作数，无解的话则返回 -1
int calc(int K) {
    memset(f, 0, sizeof(f));
    int res = 0;
    int sum = 0;
    for (int i = 0; i + K <= N; i++) {
        if ((dir[i] + sum) % 2 != 0) {
            res++;
            f[i] = 1;
        }
        sum += f[i];
        if (i - K + 1 >= 0)
            sum -= f[i - K + 1];
    }
    for (int i = N - K + 1; i < N; i++) {
        if ((dir[i] + sum) % 2 != 0)
            return -1;
        if (i - K + 1 >= 0)
            sum -= f[i - K + 1];
    }
    return res;
} 

void solve() {
    int K = 1, M = N;
    for (int k = 1; k <= N; k++) {
        int m = calc(k);
        if (m >= 0 && M > m) {
            M = m;
            K = k;
        }
    }
    printf("%d %d\n", K, M);
}

反转（开关问题）

猜你喜欢