前言

   最近在学习Munkres的《拓扑学》，其中的第一章讲述了基本的集合论与逻辑知识，虽说在之前的学习中我们已经多次用到过这里的想法和定义，但始终不太严谨，所以这次还是比较全的学习了一遍。通过这次的学习加深了对一些概念的理解，而且还发现了集合论中有许多有趣的故事。
   这篇博客主要给出一些基本的定义，并给出在集合论的发展过程中的一些好玩的故事。
   2019.05.09注：通过这几天的了解，搞懂集合论需要一个完整体系，需要从头开始建立，所以本文只是给出一些有趣的事实，并假设其余的部分均已证明，即无矛盾。

一些定义及延伸

关系

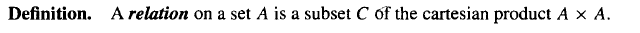
通过这种方式我们可以定义任意的关系，例如等价关系、序关系等。

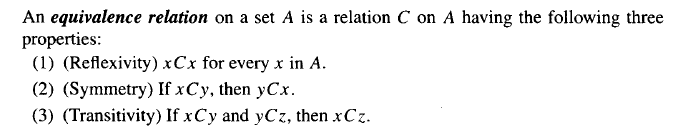
特别的，函数也是一种关系，只不过我们把集合改为了\(A \times B\)，并且给出一些特别的要求。

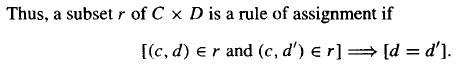
这里说的指派关系便是一个函数。

笛卡尔积

笛卡尔积可以理解为一组特定的函数，定义域为{1,2,...,m}，值域为\(A_1 \bigcup A_2 \bigcup \cdots \bigcup A_m\)，要求1只能映到\(A_1\)中，以此类推。这种方式利于我们建立\(\omega-\)笛卡尔积，即可数个集合形成的。

序数与基数

首先我们给出序数和基数的定义。

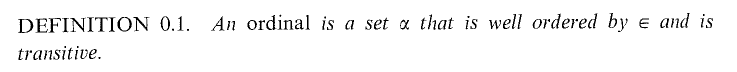
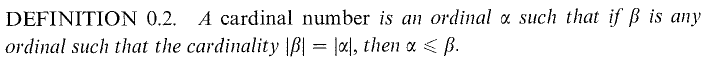
我们可以把序数理解为一些良序集的等价类，其中等价关系定义为两个良序集的序型是相似的。基数则是一种特殊的序数，使得所有与他可以建立一一映射的良序集的序数都包含他，即他是极小的。
同时我们可以把这种想法提升到数上，即把包含关系提升为\(\leq\)，这样一来就与我们之前理解的基数相同了。我们需牢记定义，但在正常使用中使用“数”这种形象的语言便可，前面的提升方式保证了我们不会导致错误。

关于势的一些结论

我们在这里不加证明的给出一些关于势的结论。

对于任意的两个集合\(X,Y\)，有\(|X| \leq |Y|\)，或者\(|X| \geq |Y|\)。
对于无限集，\(|A \bigcup B| = max\{|A|,|B|\}\)。
对于无限集，\(|X \times X| = |X|\)。
对于无限集，\(|A \times B| = max\{|A|,|B|\}\)。
对于无限集，存在他的一个真子集与他等势。
（Bernstein-Schroder定理）对于两个集合\(X,Y\)，若\(|X| \leq |Y|\)且\(|X| \geq |Y|\)，则\(|X| = |Y|\)。

选择公理与分球悖论

选择公理

选择公理是独立于ZF公理系统之外的一条公理，合称为ZFC公理系统，其表述如下:

形象的来说，便是现在有许多个装有小球的盒子，我们可以从每一个盒子中取出一个球。这在有限的情况下是平凡的，而在无限的情况下即由选择公理来保证。
选择公理有许多等价的命题，在这里不予证明的一一列出，使得我们在使用以下“定理”时，不要忘记我们已经在ZFC公理系统中了。

Zorn引理

即在一个偏序集\(A\)中，若每一个全序子集均有上界，则\(A\)中就有极大元。
Zorn引理在证明对任意的无限集\(X\)都有\(|X \times X| = |X|\)中，以及抽象代数对于极大理想的存在性证明中均有应用。

良序定理

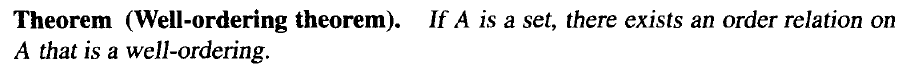
我们把满足“任一非空子集在该序关系下都有最小元”的全序集称为良序集。

Hausdorff极大原理

即在一个偏序集\(A\)中，对任意的全序子集\(B\)，均有一个极大全序子集包含\(B\)。

分球悖论

分球悖论是说，对于一个三维空间中的球，我们可以通过把他拆分，再旋转，再平移组合的方式，得到两个与之前一模一样的球。

分球悖论的提出本意为反对选择公理，因为它是通过选择公理证明的，而且其结果十分反常，与人们的经验不符，所以也显得十分有趣。在这里我们提出这个悖论，是因为他的证明十分的精彩，我们在这里只给出证明的梗概，证明的全文可在维基百科中看到。 Banach-Tarski paradox
首先，我们来观察一下由\(\{ a,b \}\)生成的自由群\(F_2\)的样子，我们把\(F\)分为四类，其中\(S(a) = \{ x \in F_2, x_1=a\}\)，\(x_1\)代表x的第一个位置。同理，我们可以得到\(S(b),S(a^{-1}),S(b^{-1})\)这样我们会得到\(F\)的一个无交分解\(F_2=\{ e\} \bigcup S(a) \bigcup S(b) \bigcup S(a^{-1}) \bigcup S(b^{-1})\)，在这几个子集中我们发现有这样的性质，\(aS(a^{-1}) \bigcup S(a) = F_2\)，\(bS(b^{-1}) \bigcup S(b) = F_2\)。这个等式与我们想要的结果已经在形式上类似了，并且一个三维空间中的所有旋转组成了一个群，这让我们希望能够发现这个群中是否包含一个两个元素生成的自由群。惊喜的是，这样的群是存在的，我们可以给出一个具体例子，但并不给出其是自由群的证明，比如令\(\theta = arctan\frac{1}{3}\)，\(a,b\)分别代表绕x轴和z轴顺时针旋转\(\theta\)角，则由\(a,b\)生成的群就是这样的一个由两个元素生成的自由群。事实上，我们只要取\(\theta\)是\(\pi\)的无理倍，并且两个旋转无关，即不能通过组合的方式回到原样，就是一组我们可以选取的\(a,b\)。我们把这个群记为\(G\)。
我们首先考虑球面\(S^2\)上的点，我们可以通过\(G\)对\(S^2\)的一个群作用，把\(S^2\)分成不同的轨道，作用方式即为旋转，这其实给出了一个等价关系，即两个点在同一个等价类中当且仅当他们中间只差\(G\)中的一个旋转。
下面我们将要使用选择公理，我们要在每一个轨道中选出一个代表元素，使他们组成一个集合，记为\(M\)，则我们有\(G \times M=S^2\)，由上，我们给出了\(S^2\)的一个无交分解\(S^2 = M \bigcup S(a)M \bigcup S(b)M \bigcup S(a^{-1})M \bigcup S(b^{-1})M\)。再根据上面讨论的该自由群的性质，我们可以对\(S^2\)进行一个分解，由于直接分解会导致\(M\)的重复，所以我们把\(S^2\)分解为以下四个部分，\(A_1 = M \bigcup S(a)M \bigcup B\)，\(A_2 = S(a^{-1})M \setminus B\)，\(A_3 = S(b)M\)，\(A_4 = S(b^{-1})M\)，其中\(B = a^{-1}M \bigcup a^{-2}M \bigcup \cdots\)，简单验证便可以发现，\(aA_2 \bigcup A_1 = S^2\)，\(bA_4 \bigcup A_3 = S^2\)。到这里，我们就完成了对球面上的分解的证明，至于对于整个球，我们只需做连接球面与球心半径的半开半闭区间，其中球心为开区间端点，便可得到最终对整个球的分解。
证明中有几个关键步骤。首先是对于\(F_2\)的性质的了解，这是令我喜悦的部分。其次是要在旋转群中找到一个这样的自由群，正因如此，我们选择了三维空间，而且这个被我们省略的步骤并不简单，需要一定的计算能力。最后就是在分解的处理上，要做合适的分解，才能使变换之后各个部分之间无交。这绝对是一个漂亮的证明。

罗素悖论

人们了解罗素悖论一般是从他的形象意义出发的，即理发师悖论：“一个理发师声称自己只为不给自己理发的人理发，那他是否为自己理发呢？”。我们再给出他的数学表达形式，记\(X=\{A| A \not\in A\}\)，那么\(X\)是否属于\(X\)呢？这个悖论的提出直接影响了ZF公理系统的建立，Zermelo也因此修改了原来的公理系统，得到现在的ZF公理系统。
我们首先给出三个我们即将用到的公理。

正则公理

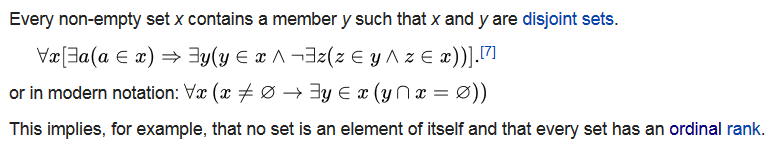
分离公理

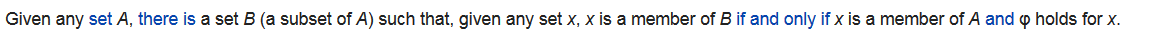
配对公理

一般来说，大多数悖论的提出都与“包含全体集合的集合有关”，所以在ZF公理系统中，我们排除了这种情况，事实上，这种包含全体集合的集合称为一个真类。下面给出通过正则公理证明不存在一个集合包含所有的集合。事实上，我们证明了不存在集合\(A\)，使得\(A \in A\)。
反证，假设\(A\)是一个满足\(A \in A\)的集合，则由配对公理，\(B=\{A\}\)是一个集合，则由正则公理，\(A \bigcap B = \emptyset\)，然而\(A \in A,A \in B\)，矛盾。
如果不存在包含所有集合的集合，那么由分离公理，我们可以知道罗素悖论中构造的集合\(X\)不复存在，这是因为没有任何一个已知集合可以包含\(X\)中的元素。

总结

集合论的公理化是一个漫长的过程，最好有一个大致的了解，使得之后的学习中每一步都走得自信起来。

好玩的集合论

前言