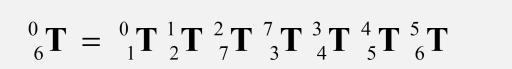2. 操作臂运动学

本文链接： https://blog.csdn.net/m0_37570854/article/details/96496056

1.概述

1.1 连杆

操作臂可以看成是一系列刚体通过关节连接而成的一个串行运动链，这些刚体称为连杆。常见的连杆有转动和移动关节的。为每个连杆建立一个固连坐标系，包括基坐标系，n个关节机器人一共有n个关节、n个连杆，n+1个·坐标系。空间物体的自由度最多是6个，因此6关节机器人即可实现操作端在空间的6自由度运动：3个自由度用于确定操作端位置，另外3个自由度用于确定操作端姿态，操作端的位姿由6个关节可以完全确定。少于6个自由度是欠驱动操作臂，多余6个自由度的是冗余驱动操作臂。从操作臂的基座开始为连杆编号，固定基座看作连杆0，以此类推，最末端连杆为连杆n 。

为描述每个连杆与相邻连杆之间的相对位置关系，需要在每个连杆上定义一个固连坐标系。固连在连杆i上的坐标系称为坐标系{i}。

1.2 连杆附加坐标系的规定

连杆i参照关节轴i运动（沿其转动或直线移动），坐标系{i}的Z轴与关节轴i重合，方向可任意确定；两条相邻Z轴存在公垂线，称 $z_{i-1}$ 与 $z_i$ 的公垂线为 $z_i$ 的前公垂线，另一条为 $z_i$ 的后公垂线。如相邻Z轴平行，选任意一条公垂线即可。

{i}坐标系的原点位于其后公垂线与 $z_i$ 的交点处；

{i}坐标系的 $x_i$ 沿后公垂线指向关节轴i+1。如 $z_i$ 与 $z_{i+1}$ 相交，则可任意选择后公垂线上一个方向。

{i}坐标系的 $y_i$ 轴由右手定则根据 $x_i$ 和 $z_i$ 确定。

2.D-H参数

2.1连杆的4 个参数：

扫描二维码关注公众号，回复： 7219353 查看本文章

1、连杆长度：关节轴i-1同关节轴i 的公垂线长度定义为连杆i-1的长度 $a_{i-1}$ ，也即关节轴i-1沿移动直至与关节轴i相交（重合）的距离。

2、连杆转角：绕图中轴 $x_{i-1}$ ，按右手法则旋转关节轴i-1，使其与关节轴i平行，转动角度为连杆转角 $\alpha_{i-1}$ 。

3、连杆偏距：沿 $z_i$ 方向，关节轴i上前公垂线交点到后公垂线交点的位移 $d_i$ 。

4、关节角：绕图中 $z_i$ 轴按右手法则旋转前公垂线，使其与 $x_i$ 轴平行，转动角位移为关节角 $\theta_i$ 。

注意： $d_i$ 与 $\theta_i$ 当中至多有一个是关节变量。

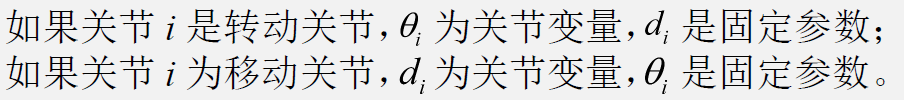
最后，在总结一下：

举个例子：

2.2 连杆坐标系变换

连杆坐标系变换 $_{i}^{i-1}\textrm{T}$ （{i-1}→{i}）的推导采用相对组合变换:

1) 从i-1坐标系出发，绕 $x_{i-1}$ 旋转 $\alpha_{i-1}$ 角，使 $z_{i-1}^'$ 与 $z_i$ 同方向。

2）沿 $x_{i-1}^{'}$ 平移 $a_{i-1}$ ，使 $z_{i}^{''}$ 与 $z_{i}$ 重合

3）再绕 $z_{i-1}^{''}$ 旋转 $\theta_{i}$ ，使变换后的 $x_{i-1}^{'''}$ 与 $x_{i}$ 同方向

4）在沿 $z_{i-1}^{'''}$ 平移 $d_i$ ，使变换后的坐标系与 $i$ 坐标系重合。

则：

$_{i-1}^{i}\textrm{T}=Rot(x,\alpha_{i-1})Trans(a_{i-1},0,0)Rot(z,\theta_{i})Trans(0,0,d_i)$

$Rot(x,\alpha_{i-1})=\begin{bmatrix} 1 & 0 & 0 &0 \\ 0& c\alpha_{i-1} & -s\alpha_{i-1} &0 \\ 0 & s\alpha_{i-1}& c\alpha_{i-1} &0 \\ 0&0 & 0 &1 \end{bmatrix}$ $Trans(a_{i-1},0,0)=\begin{bmatrix} 1 &0 & 0 & a_{i-1}\\ 0& 1 & 0&0 \\ 0& 0 & 1&0 \\ 0& 0 &0 & 1 \end{bmatrix}$

$Rot(z,\theta_{i})=\begin{bmatrix} c\theta_{i} & -s\theta_{i} & 0 &0 \\ s\theta_{i} &c\theta_{i} & 0 &0 \\ 0& 0 &1 &0 \\ 0&0 & 0 & 1 \end{bmatrix}$ $Trans(0,0,d_{i})=\begin{bmatrix} 1 & 0 & 0&0 \\ 0 & 1 & 0 & 0\\ 0& 0&1 & d_i\\ 0& 0 & 0 & 1 \end{bmatrix}$

$_{i-1}^{i}\textrm{T}=Rot(x,\alpha_{i-1})Trans(a_{i-1},0,0)Rot(z,\theta_{i})Trans(0,0,d_i)$

$=\begin{bmatrix} c\theta_{i} & -s\theta_{i}& 0 &a_{i-1} \\ s\theta_{i}c\alpha_{i-1} &c\theta_{i}c\alpha_{i-1} & -s\alpha_{i-1} &-s\alpha_{i-1}d_i \\ s\theta_{i}s\alpha_{i-1} & c\theta_{i}s\alpha_{i-1} & c\alpha_{i-1} &c\alpha_{i-1}d_i \\ 0 & 0 &0 &1 \end{bmatrix}$

2.3 操作臂的正向运动学

计算坐标系{n}相对于坐标系{0}的变换矩阵（一系列相对组合变换）： $_{n}^{0}\textrm{T}=_{1}^{0}\textrm{T}_{2}^{1}\textrm{T}...._{n}^{n-1}\textrm{T}$

变换矩阵 $_{n}^{0}\textrm{T}$ 是关于n个变量（旋转变量 $\theta_i$ 或移动变量 $d_i$ ）的函数。如能测量得到操作臂关节变量的值，就可以根据变换矩阵 $_{n}^{0}\textrm{T}$ 计算出末端连杆坐标系在笛卡儿空间中的位置和姿态。

这就是操作臂的正向运动学计算。

举例：

D-H参数表：

PUMA560 1-3轴的连杆坐标转换矩阵：

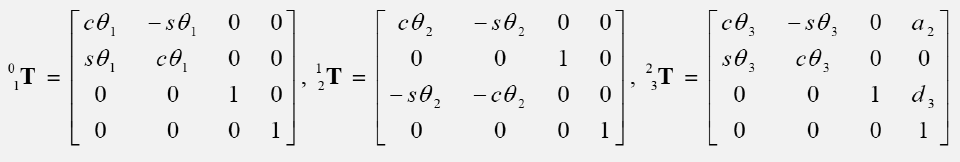
再举个例子：

D-H参数表：

i	$\alpha_{i-1}$	$a_{i-1}$	$d_{i}$	$\theta_{i}$
1	0	0	0	$\theta_1$	$_{1}^{0}\textrm{T}$
2	$-90^{\circ}$	$0$	$0$	$\theta_{2}$	$_{2}^{1}\textrm{T}$
7	$90^{\circ}$	$0$	$520$	$\theta_{7}$	$_{7}^{2}\textrm{T}$
3	$-90^{\circ}$	$0$	$0$	$\theta_{3}$	$_{3}^{7}\textrm{T}$
4	$90^{\circ}$	$0$	$390$	$\theta_{4}$	$_{4}^{3}\textrm{T}$
5	$-90^{\circ}$	$0$	$0$	$\theta_{5}$	$_{5}^{4}\textrm{T}$
6	$90^{\circ}$	$0$	$0$	$\theta_{6}$	$_{6}^{5}\textrm{T}$

1.概述

2.D-H参数

猜你喜欢