题意:给你一个数列$Ai$和一个数字$m$,对于每个$1<=x<=m$,计算$\sum_{i=1}^{n} \lfloor\frac{x}{ai}\rfloor+\lfloor\frac{ai}{x}\rfloor$,把每个x的答案异或起来输出
首先分成两部分算,看到除法、下取整让人联想到数论分块,不妨手玩一下:
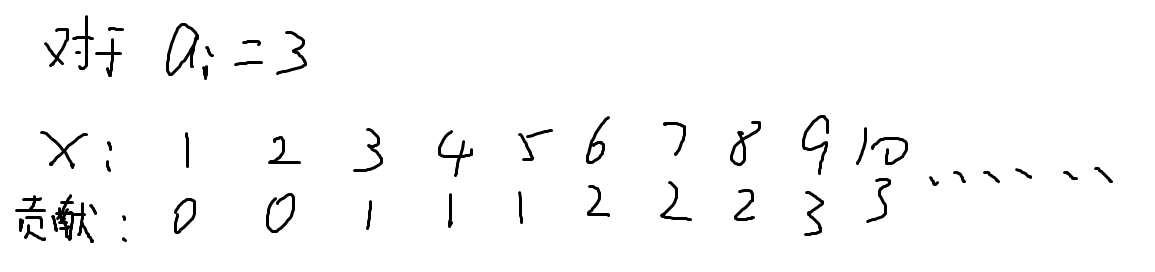
可以看到我们不仅可以考虑$ai$对每个$x$答案的贡献,还会发现$x$在是$ai$的k倍时产生的贡献会+1,之后持续一段
类似数论分块,再加上单点修改区间查询,使用树状数组到$nlog(n)$:(来自ZTB学长的博客)
一种枚举这个不同取值的方法是:
for(int i=1,pos;i<=N;i=pos+1){ pos=N/(N/i);// 这里保证了[i,pos]除N下取整的值都一样 /*...*/ }复杂度 $O(N\sqrt{N}log(N))$,期望得分20分,常数小可以得到60分。
既然只在最后查询一次,只要在转折点打个标记再求前缀和就可以了!复杂度$O(n\sqrt{n})$
如果觉得∑i=1N⌊√i⌋很小,能过N≤3×106
(一开始我也这么觉得),我跑了一下,这个数字是3462603142,实际上是O(N√N)这个级别。
懒得写了...(但是还是要改latex)
算法四
根号算法都吃屎吧!现在我们单看⌊xAi⌋。我们发现当x从k×Ai−1变为k×Ai时,这个值多了1。所以我们可以对于每个Ai,枚举它的倍数,然后往这个倍数的位置打上+1的标记,最后前缀和。
复杂度为∑i=1N⌊N / Ai⌋=O(N2)(当Ai都很小时)。
改进一下,如果有多个Ai的值相同,那么我们记下来对于每个1≤y≤N,Ai=y的次数cnt[y](就是Ai的出现次数)。这样我们可以改为对于每个1≤y≤N,枚举y的倍数,然后一次就打+cnt[y]+cnt[y]的标记。
复杂度为∑i=1N⌊N / i⌋=O(NlogN)。
⌊Ai / x⌋的话相似,改为一个Ai的区间向x的单点打标记。期望得分100分。
WDNMD公式全挂了
不伺候了
想看的时候到编辑里面看吧
#include<bits/stdc++.h> #define lbt(x) (x&-x) #define ll long long using namespace std; const int maxn=3000009; inline int read(){ int ret=0,fix=1;char ch; while(!isdigit(ch=getchar()))fix=ch=='-'?-1:fix; do ret=(ret<<1)+(ret<<3)+ch-'0'; while(isdigit(ch=getchar())); return ret*fix; } int n,mod; int a[maxn],b[maxn]; ll ans; ll t[maxn]; int main(){ scanf("%d%d",&n,&mod); if(n<200000)for(int i=1;i<=n;i++)a[i]=read(); else { a[1]=read(); for(int i=2;i<=n;i++)a[i]=((ll)a[i-1]*a[i-1]+7*a[i-1]+34221)%mod+1; } for(int i=1;i<=n;i++)b[a[i]]++; for(int i=1;i<=mod;i++){//枚举a的值 if(b[i])for(int k=1;k*i<=mod;k++)t[k*i]+=b[i]; } for(int i=1;i<=mod;i++)t[i]+=t[i-1]; for(int i=1;i<=mod;i++)b[i]+=b[i-1]; for(int i=1;i<=mod;i++){//枚举x的值 for(int k=1;k*i<=mod;k++){ int r=min((k+1)*i-1,mod); t[i]+=(ll)(b[r]-b[k*i-1])*k; } } for(int i=1;i<=mod;i++)ans^=t[i]; printf("%lld",ans); }